人教版数学八年级上册12.2全等三角形的判定课件(第3课时 共31张PPT)
文档属性
| 名称 | 人教版数学八年级上册12.2全等三角形的判定课件(第3课时 共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 373.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 15:59:57 | ||
图片预览



文档简介
我们这节课继续探索三角形全等的条件.
(2) 三条边
(1) 三个角
(3) 两边一角
(4) 两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
复习引入
SAS
SSA ?
人教版八年级数学上册
第十二章 全等三角形
12.2 全等三角形的判定
第3课时 “ 角边角”和“角角边”
A
B
C
D
E
F
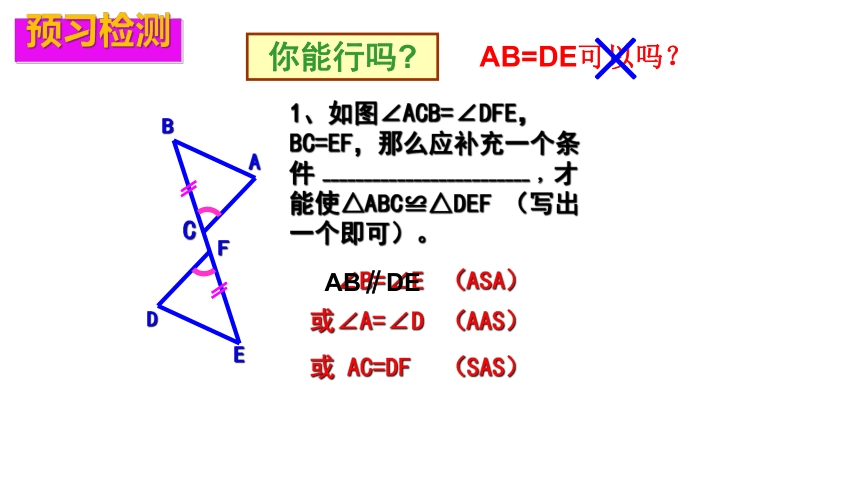
1、如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。
∠B=∠E
或∠A=∠D
或 AC=DF
你能行吗?
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
预习检测
1.经历探索三 角形全等的判定方法“ASA”
“AAS”的过程.
2.应用“AAS”“ASA”判定两个三角形全等.
3.能根据题目中的已知条件,选择不同的判定方法判定两个三角形全等.
重点:利用“ASA"“AAS"判定两个三角形全等.
难点:三角形全等的判定方法“ASA”的探索过程.
学习目标
重点难点
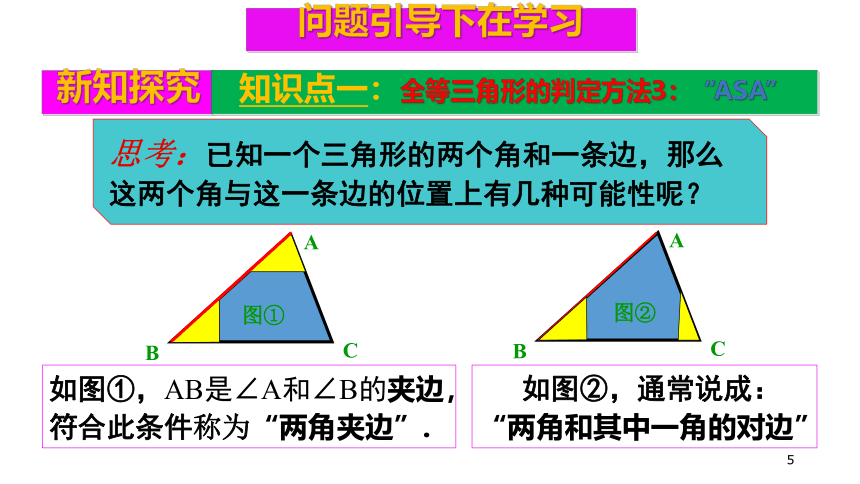
思考:已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置上有几种可能性呢?
A
B
C
A
B
C
图①
图②
如图①,AB是∠A和∠B的夹边,
符合此条件称为“两角夹边”.
如图②,通常说成:
“两角和其中一角的对边”
新知探究
知识点一:全等三角形的判定方法3:“ASA”
问题引导下在学习
新知探究
知识点一:全等三角形的判定方法3:“ASA”
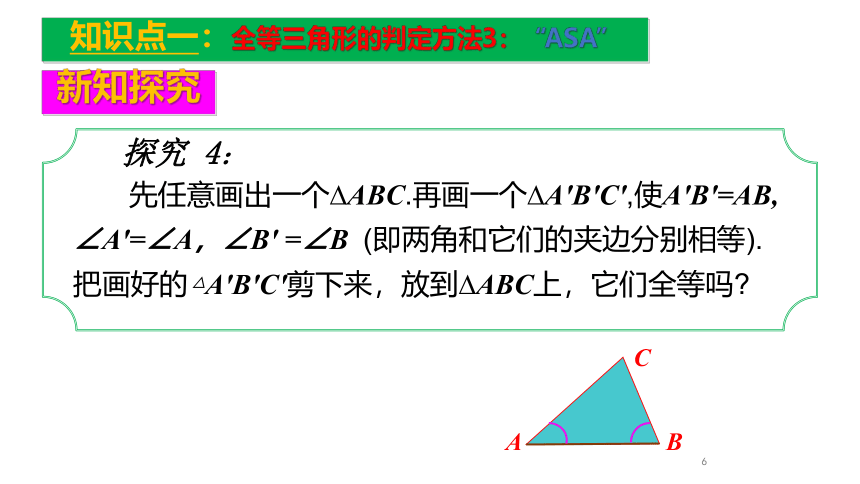
探究 4:
先任意画出一个?ABC.再画一个?A'B'C',使A'B'=AB, ∠A'=∠A,∠B' =∠B (即两角和它们的夹边分别相等).把画好的△A'B'C'剪下来,放到?ABC上,它们全等吗?
B
A
C
新知探究
知识点一:全等三角形的判定方法3:“ASA”
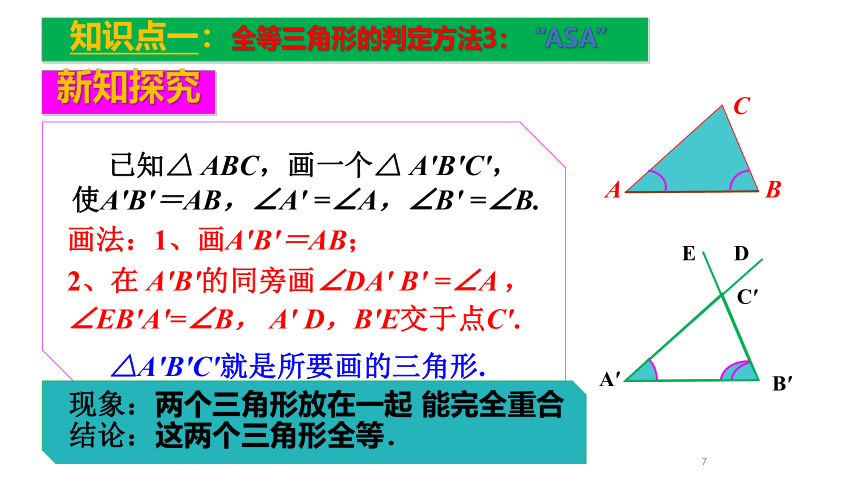
已知△ ABC,画一个△ A′B′C′,使A′B′=AB,∠A′ =∠A,∠B′ =∠B.
画法:1、画A′B′=AB;
2、在 A′B′的同旁画∠DA′ B′ =∠A ,
∠EB′A′=∠B, A′ D,B′E交于点C′.
△A′B′C′就是所要画的三角形.
B
A
C
A′
B′
C′
E
D
现象:两个三角形放在一起 能完全重合
结论:这两个三角形全等.
新知探究
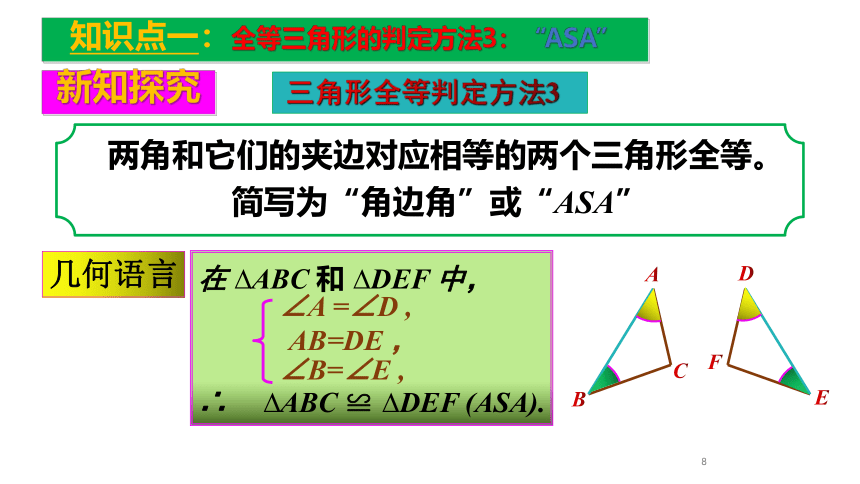
知识点一:全等三角形的判定方法3:“ASA”
三角形全等判定方法3
两角和它们的夹边对应相等的两个三角形全等。
简写为“角边角”或“ASA”
几何语言
在 ?ABC 和 ?DEF 中,
∴ ?ABC ≌ ?DEF (ASA).
∠A =∠D ,
F
E
D
C
B
A
∠B=∠E ,
AB=DE ,
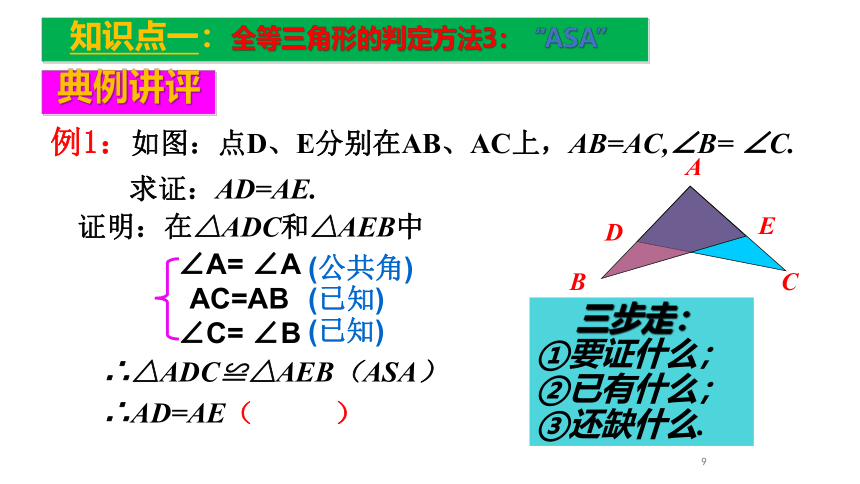
典例讲评
知识点一:全等三角形的判定方法3:“ASA”
例1:如图:点D、E分别在AB、AC上,AB=AC,∠B= ∠C.
求证:AD=AE.
A
B
C
D
E
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
三步走:
①要证什么;
②已有什么;
③还缺什么.
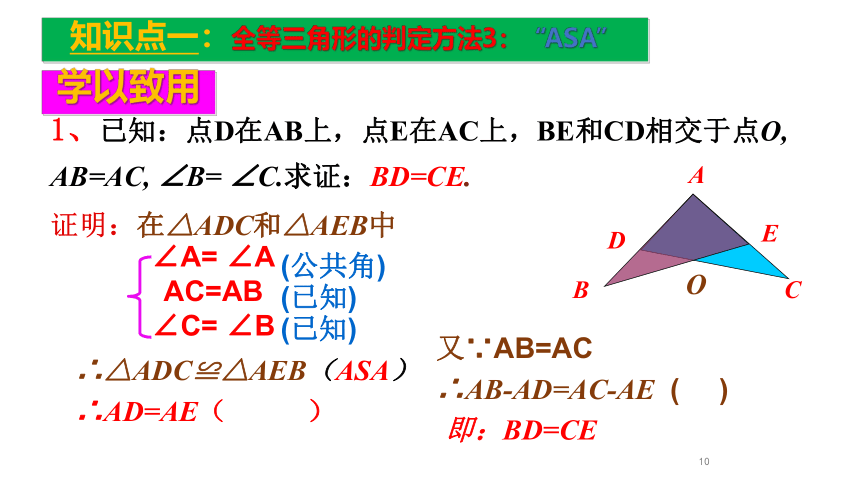
知识点一:全等三角形的判定方法3:“ASA”
1、已知:点D在AB上,点E在AC上,BE和CD相交于点O,
AB=AC, ∠B= ∠C.求证:BD=CE.
又∵AB=AC
即:BD=CE
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
( )
∴AB-AD=AC-AE
A
B
C
D
E
O
学以致用
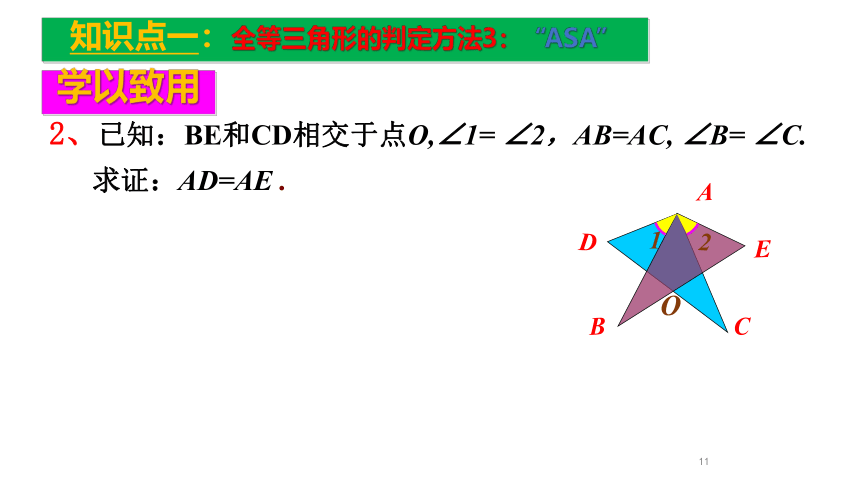
知识点一:全等三角形的判定方法3:“ASA”
A
B
C
D
E
1
2
2、已知:BE和CD相交于点O,∠1= ∠2,AB=AC, ∠B= ∠C.
求证:AD=AE .
O
学以致用
学以致用
知识点一:全等三角形的判定方法3:“ASA”
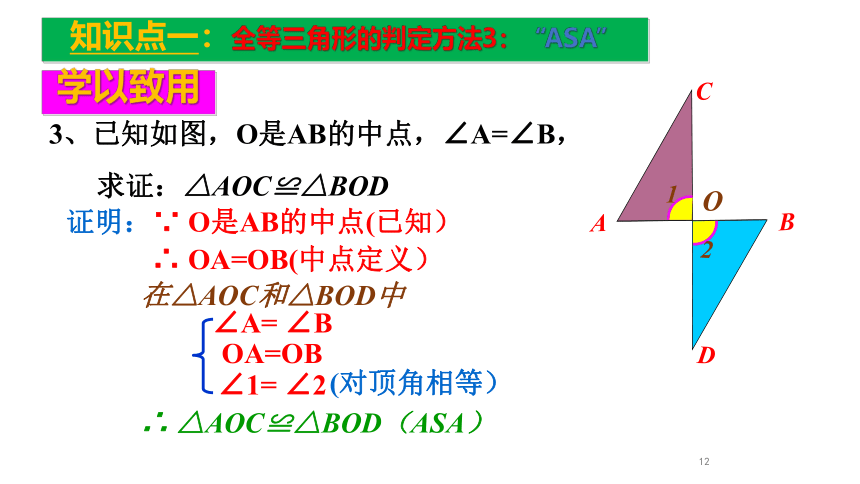
3、已知如图,O是AB的中点,∠A=∠B,
求证:△AOC≌△BOD
证明:∵ O是AB的中点(已知)
∴ OA=OB(中点定义)
在△AOC和△BOD中
∠A= ∠B
OA=OB
∠1= ∠2
(对顶角相等)
∴ △AOC≌△BOD(ASA)
A
B
C
D
O
1
2
学以致用
知识点一:全等三角形的判定方法3:“ASA”
4、小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?
(2)
(1)
两角的大小和它们的夹边的长度确定了,这个三角形的形状和大小也就确定了.
先独立完成导学案互动探究1,再同桌相互交
流,最后小组交流;
合作探究
知识点一:全等三角形的判定方法3:“ASA”
归纳总结
常见的隐含的等角有:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角点等角的余(补)角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线得到同位角或内错角相等.另外,“太阳光线可以看成是平行的”、“光的反射角等于入射角”等也是常见的隐含条件.
知识点一:全等三角形的判定方法3:“ASA”
新知探究
知识点二:全等三角形的判定方法4:“AAS”
例2:如下图,在△ABC和△DEF中,
∠A =∠D, ∠ B=∠E, BC=EF,
求证:△ABC≌△DEF.
E
F
D
证明:在△ABC中,
∠C=180°-∠A -∠B ,
同理 ∠F=180°-∠D -∠E,
又∵ ∠A =∠D, ∠B=∠E,
∴ ∠C=∠F,
在△ABC和△DEF中,
∴ ∠B=∠E,
BC=EF,
∠C=∠F,
∴ △ABC ≌△DEF (ASA)
B
A
C
知识点二:全等三角形的判定方法4:“AAS”
新知探究
三角形全等判定方法4
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写为“角角边”或“AAS”
几何语言
在 ?ABC 和 ?DEF 中,
∴ ?ABC ≌ ?DEF (AAS).
∠A =∠D ,
F
E
D
C
B
A
∠B=∠E ,
AC=DF ,
先独立完成导学案互动探究3,再同桌相互交流,最后小组交流;
合作探究
知识点二:全等三角形的判定方法4:“AAS”
学以致用
知识点二:全等三角形的判定方法4:“AAS”
1.如图,∠ABC=∠DEF,AB=DE,
要说明△ABC≌△DEF,
(1)若以“SAS”为依据,还需添加的条件为 ;
(2)若以“ASA”为依据,还需添加的条件为 ;
(3)若以“AAS”为依据,还需添加的条件
为 .
B
A
C
E
F
D
BC=EF或BE=FC
∠A =∠D
∠ACB=∠DFE或AC∥DF
知识点二:全等三角形的判定方法4:“AAS”
学以致用
2、已知如图, ∠1=∠2,
求证:AD=AC.
1
A
B
D
C
2
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴ AD=AC
∠C=∠D
3
4
∠3=∠4
学以致用
知识点二:全等三角形的判定方法4:“AAS”
3、已知:点D在AB上,点E在AC上,BE和CD相交于点O,
AB=AC, ∠B= ∠C.求证:OB=OC.
A
B
C
D
E
O
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
又∵AB=AC
即:BD=CE……
( )
∴AB-AD=AC-AE
三步走:
①要证什么;
②已有什么;
③还缺什么.
知识点二:全等三角形的判定方法4:“AAS”
A
B
C
D
E
1
2
4、如图,AE⊥BE,AD⊥DC,CD =BE,∠1 =∠2.
求证:AB =AC.
学以致用
A
C
D
B
1. 如图, AB⊥BC, AD⊥DC,∠1=∠2,
求证AB=AD.
1
2
达标检测
例2:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B= ∠C
求证:AD=AE.
B
A
E
C
D
O
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
又∵AB=AC
∴BD=CE
(全等三角形的对应边相等)
(已知)
(等式性质1)
BD=CE吗?
2、如图,要测量河两岸相对两点A,B两
点的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A,C,E在一条直线上,这时
测得DE的长就是AB的长,为什么?
A
B
C
D
E
F
1、如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。
A
B
C
D
E
F
考考你
证明:∵ BE=CF(已知)
∴BC=EF(等式性质)
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
∵ AB∥DE AC∥DF (已知)
∴ ∠B=∠DEF , ∠ACB=∠F
归纳总结
知识点二:全等三角形的判定方法4:“AAS”
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
“S”的意义
书写格式
联系
ASA
AAS
“ASA”与“AAS”的区别与联系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}“S ”是两角夹边
“S ”是其中一角的对边
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}把夹边相等写在两角相等的中间
把两角相等写在一起,边相等写在最后
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由三角形内角和定理可知,“ASA”与”AAS”可互相转化
归纳总结
知识点二:全等三角形的判定方法4:“AAS”
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}相等的边或角
是否全等
简写
三个角
三条边
两边一角
两角一边
?
?
?
?
?
?
SSS
SAS
ASA
AAS
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两边夹角
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两边与一边对角
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两角夹边
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两角与一角对边
思维导图
全等三角形的判定
方法1:边边边 (SSS)
方法2:边角边 (SAS)
方法3:角边角 (ASA)
方法4:角角边 (AAS)
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第41页练习以及习题12.2第4、5、9--12题;
2.《导学测评》;
作业布置
(2) 三条边
(1) 三个角
(3) 两边一角
(4) 两角一边
当两个三角形满足六个条件中的三个时,有四种情况:
SSS
不能!
?
复习引入
SAS
SSA ?
人教版八年级数学上册
第十二章 全等三角形
12.2 全等三角形的判定
第3课时 “ 角边角”和“角角边”
A
B
C
D
E
F
1、如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ------------------------- ,才能使△ABC≌△DEF (写出一个即可)。
∠B=∠E
或∠A=∠D
或 AC=DF
你能行吗?
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
预习检测
1.经历探索三 角形全等的判定方法“ASA”
“AAS”的过程.
2.应用“AAS”“ASA”判定两个三角形全等.
3.能根据题目中的已知条件,选择不同的判定方法判定两个三角形全等.
重点:利用“ASA"“AAS"判定两个三角形全等.
难点:三角形全等的判定方法“ASA”的探索过程.
学习目标
重点难点
思考:已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置上有几种可能性呢?
A
B
C
A
B
C
图①
图②
如图①,AB是∠A和∠B的夹边,
符合此条件称为“两角夹边”.
如图②,通常说成:
“两角和其中一角的对边”
新知探究
知识点一:全等三角形的判定方法3:“ASA”
问题引导下在学习
新知探究
知识点一:全等三角形的判定方法3:“ASA”
探究 4:
先任意画出一个?ABC.再画一个?A'B'C',使A'B'=AB, ∠A'=∠A,∠B' =∠B (即两角和它们的夹边分别相等).把画好的△A'B'C'剪下来,放到?ABC上,它们全等吗?
B
A
C
新知探究
知识点一:全等三角形的判定方法3:“ASA”
已知△ ABC,画一个△ A′B′C′,使A′B′=AB,∠A′ =∠A,∠B′ =∠B.
画法:1、画A′B′=AB;
2、在 A′B′的同旁画∠DA′ B′ =∠A ,
∠EB′A′=∠B, A′ D,B′E交于点C′.
△A′B′C′就是所要画的三角形.
B
A
C
A′
B′
C′
E
D
现象:两个三角形放在一起 能完全重合
结论:这两个三角形全等.
新知探究
知识点一:全等三角形的判定方法3:“ASA”
三角形全等判定方法3
两角和它们的夹边对应相等的两个三角形全等。
简写为“角边角”或“ASA”
几何语言
在 ?ABC 和 ?DEF 中,
∴ ?ABC ≌ ?DEF (ASA).
∠A =∠D ,
F
E
D
C
B
A
∠B=∠E ,
AB=DE ,
典例讲评
知识点一:全等三角形的判定方法3:“ASA”
例1:如图:点D、E分别在AB、AC上,AB=AC,∠B= ∠C.
求证:AD=AE.
A
B
C
D
E
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
三步走:
①要证什么;
②已有什么;
③还缺什么.
知识点一:全等三角形的判定方法3:“ASA”
1、已知:点D在AB上,点E在AC上,BE和CD相交于点O,
AB=AC, ∠B= ∠C.求证:BD=CE.
又∵AB=AC
即:BD=CE
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
( )
∴AB-AD=AC-AE
A
B
C
D
E
O
学以致用
知识点一:全等三角形的判定方法3:“ASA”
A
B
C
D
E
1
2
2、已知:BE和CD相交于点O,∠1= ∠2,AB=AC, ∠B= ∠C.
求证:AD=AE .
O
学以致用
学以致用
知识点一:全等三角形的判定方法3:“ASA”
3、已知如图,O是AB的中点,∠A=∠B,
求证:△AOC≌△BOD
证明:∵ O是AB的中点(已知)
∴ OA=OB(中点定义)
在△AOC和△BOD中
∠A= ∠B
OA=OB
∠1= ∠2
(对顶角相等)
∴ △AOC≌△BOD(ASA)
A
B
C
D
O
1
2
学以致用
知识点一:全等三角形的判定方法3:“ASA”
4、小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?
(2)
(1)
两角的大小和它们的夹边的长度确定了,这个三角形的形状和大小也就确定了.
先独立完成导学案互动探究1,再同桌相互交
流,最后小组交流;
合作探究
知识点一:全等三角形的判定方法3:“ASA”
归纳总结
常见的隐含的等角有:①公共角相等;②对顶角相等;③等角加(或减)等角,其和(或差)仍相等;④同角点等角的余(补)角相等;⑤由角平分线的定义得出角相等;⑥由垂直的定义得出角相等;⑦由平行线得到同位角或内错角相等.另外,“太阳光线可以看成是平行的”、“光的反射角等于入射角”等也是常见的隐含条件.
知识点一:全等三角形的判定方法3:“ASA”
新知探究
知识点二:全等三角形的判定方法4:“AAS”
例2:如下图,在△ABC和△DEF中,
∠A =∠D, ∠ B=∠E, BC=EF,
求证:△ABC≌△DEF.
E
F
D
证明:在△ABC中,
∠C=180°-∠A -∠B ,
同理 ∠F=180°-∠D -∠E,
又∵ ∠A =∠D, ∠B=∠E,
∴ ∠C=∠F,
在△ABC和△DEF中,
∴ ∠B=∠E,
BC=EF,
∠C=∠F,
∴ △ABC ≌△DEF (ASA)
B
A
C
知识点二:全等三角形的判定方法4:“AAS”
新知探究
三角形全等判定方法4
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写为“角角边”或“AAS”
几何语言
在 ?ABC 和 ?DEF 中,
∴ ?ABC ≌ ?DEF (AAS).
∠A =∠D ,
F
E
D
C
B
A
∠B=∠E ,
AC=DF ,
先独立完成导学案互动探究3,再同桌相互交流,最后小组交流;
合作探究
知识点二:全等三角形的判定方法4:“AAS”
学以致用
知识点二:全等三角形的判定方法4:“AAS”
1.如图,∠ABC=∠DEF,AB=DE,
要说明△ABC≌△DEF,
(1)若以“SAS”为依据,还需添加的条件为 ;
(2)若以“ASA”为依据,还需添加的条件为 ;
(3)若以“AAS”为依据,还需添加的条件
为 .
B
A
C
E
F
D
BC=EF或BE=FC
∠A =∠D
∠ACB=∠DFE或AC∥DF
知识点二:全等三角形的判定方法4:“AAS”
学以致用
2、已知如图, ∠1=∠2,
求证:AD=AC.
1
A
B
D
C
2
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴ AD=AC
∠C=∠D
3
4
∠3=∠4
学以致用
知识点二:全等三角形的判定方法4:“AAS”
3、已知:点D在AB上,点E在AC上,BE和CD相交于点O,
AB=AC, ∠B= ∠C.求证:OB=OC.
A
B
C
D
E
O
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
( )
又∵AB=AC
即:BD=CE……
( )
∴AB-AD=AC-AE
三步走:
①要证什么;
②已有什么;
③还缺什么.
知识点二:全等三角形的判定方法4:“AAS”
A
B
C
D
E
1
2
4、如图,AE⊥BE,AD⊥DC,CD =BE,∠1 =∠2.
求证:AB =AC.
学以致用
A
C
D
B
1. 如图, AB⊥BC, AD⊥DC,∠1=∠2,
求证AB=AD.
1
2
达标检测
例2:
已知:点D在AB上,点E在AC上,BE和CD相交于点O,AB=AC, ∠B= ∠C
求证:AD=AE.
B
A
E
C
D
O
证明:在△ADC和△AEB中
∠A= ∠A
AC=AB
∠C= ∠B
(公共角)
(已知)
(已知)
∴△ADC≌△AEB(ASA)
∴AD=AE
又∵AB=AC
∴BD=CE
(全等三角形的对应边相等)
(已知)
(等式性质1)
BD=CE吗?
2、如图,要测量河两岸相对两点A,B两
点的距离,可以在AB的垂线BF上取两点
C,D,使BC=CD,再定出BF的垂线
DE,使A,C,E在一条直线上,这时
测得DE的长就是AB的长,为什么?
A
B
C
D
E
F
1、如图:已知AB∥DE,AC∥DF,BE=CF。求证:△ABC≌△DEF。
A
B
C
D
E
F
考考你
证明:∵ BE=CF(已知)
∴BC=EF(等式性质)
∠B=∠E
在△ABC和△DEF中
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
∵ AB∥DE AC∥DF (已知)
∴ ∠B=∠DEF , ∠ACB=∠F
归纳总结
知识点二:全等三角形的判定方法4:“AAS”
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
“S”的意义
书写格式
联系
ASA
AAS
“ASA”与“AAS”的区别与联系:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}“S ”是两角夹边
“S ”是其中一角的对边
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}把夹边相等写在两角相等的中间
把两角相等写在一起,边相等写在最后
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}由三角形内角和定理可知,“ASA”与”AAS”可互相转化
归纳总结
知识点二:全等三角形的判定方法4:“AAS”
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}相等的边或角
是否全等
简写
三个角
三条边
两边一角
两角一边
?
?
?
?
?
?
SSS
SAS
ASA
AAS
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两边夹角
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两边与一边对角
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两角夹边
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}两角与一角对边
思维导图
全等三角形的判定
方法1:边边边 (SSS)
方法2:边角边 (SAS)
方法3:角边角 (ASA)
方法4:角角边 (AAS)
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
1.课本第41页练习以及习题12.2第4、5、9--12题;
2.《导学测评》;
作业布置
