人教版数学八年级上册12.2.1全等三角形的判定(一)(30张)
文档属性
| 名称 | 人教版数学八年级上册12.2.1全等三角形的判定(一)(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
全等三角形的判定(一)
预习检测:
1、判断两个三角形全等至少需要_ 条件。
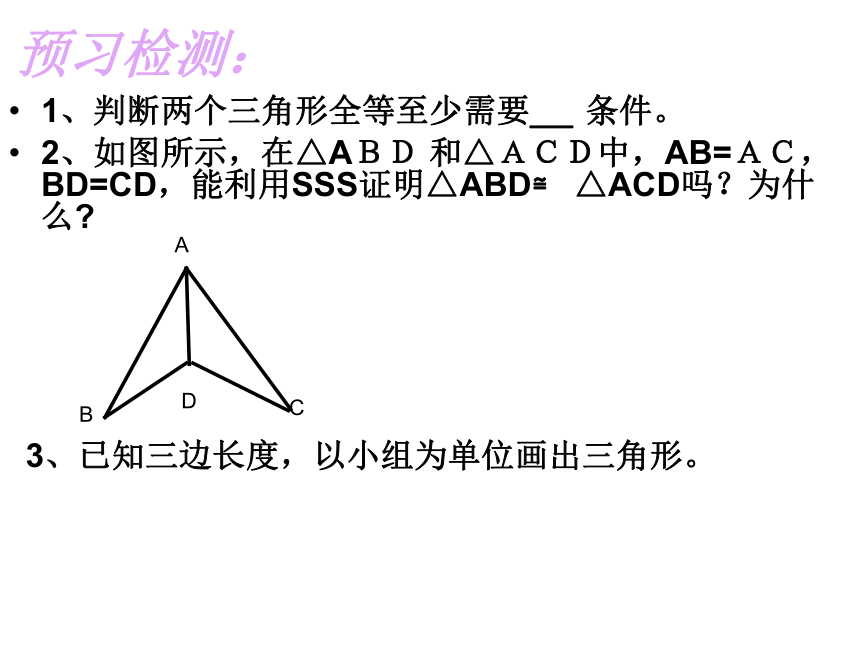
2、如图所示,在△ABD 和△ACD中,AB=AC,BD=CD,能利用SSS证明△ABD≌ △ACD吗?为什么
A
B
C
D
3、已知三边长度,以小组为单位画出三角形。
1.掌握 “SSS”判定两个三角形全等.
2.经历对应条件下两个三角形全等的探究过程,让学生体会分类的思想.
3.通过图形变换,培养学生观察——思考——总结的良好思维习惯.
4.核心素养目标:培养学生几何直观、数学抽象以及逻辑推理的核心素养。
学习目标
1. 准确找出两个三角形的对应边、对应角
2. 规范书写全等三角形的证明过程
边边边的发现过程及辨析
教学重点
教学难点
(一)创设情境,提出问题
教学过程
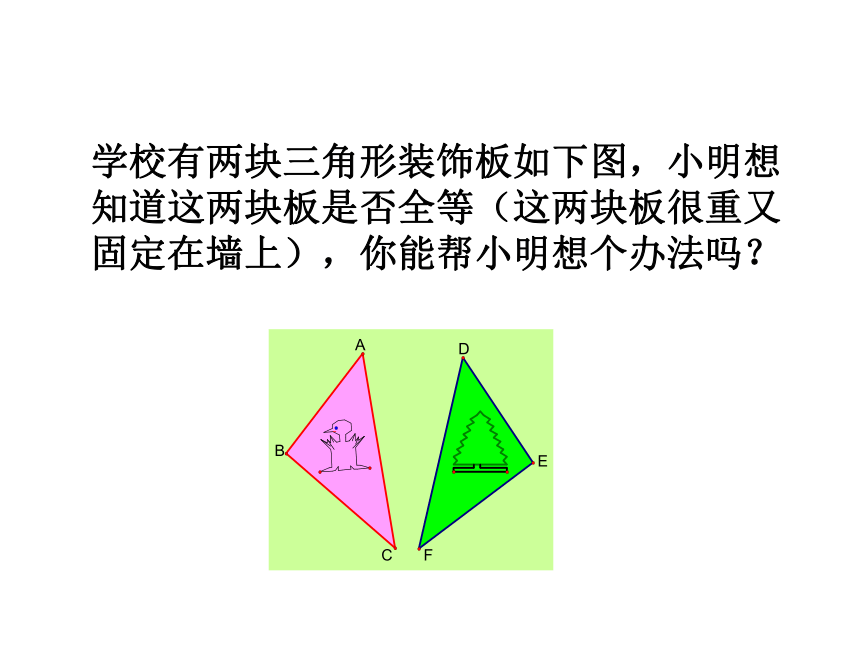
学校有两块三角形装饰板如下图,小明想知道这两块板是否全等(这两块板很重又固定在墙上),你能帮小明想个办法吗?
(二)讨论探究,解决问题
探究用较少的条件来说明两个三角形全等。
角、边
一个角对应相等
一条边对应相等
一个角,一条边分别对应相等
两条边对应相等
两个角对应相等
三个角对应相等
三条边对应相等
两角一边对应相等、两边一角对应相等
分类得出不同的情况
1.一个条件.
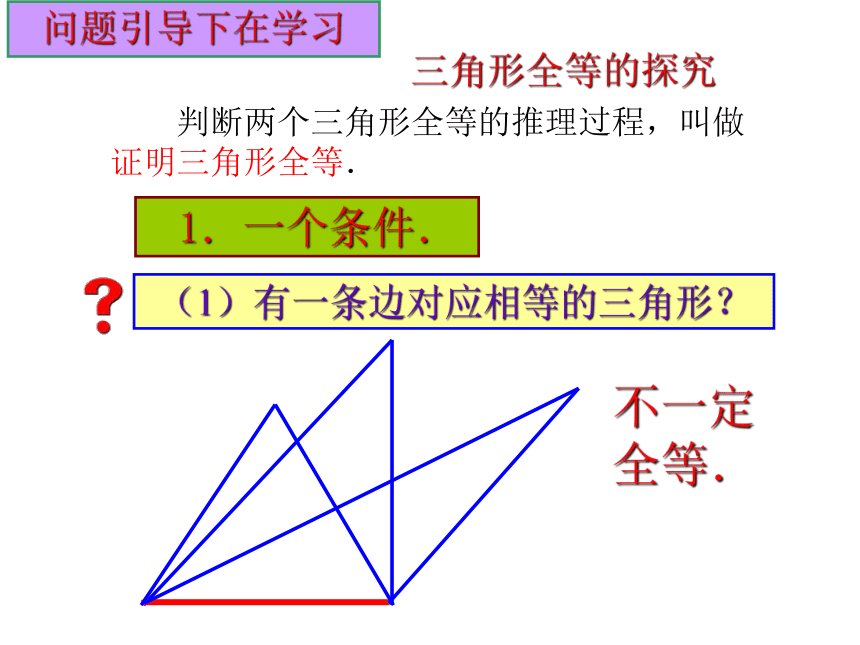
(1)有一条边对应相等的三角形?
不一定全等.
三角形全等的探究
判断两个三角形全等的推理过程,叫做证明三角形全等.
问题引导下在学习
(2)有一个角对应相等的三角形?
一个条件,并不能保证三角形全等.
不一定全等.
结论
不一定全等.
(1) 三角形的一个角和一条边对应相等的三角形?
2.两个条件.
(2)三角形的两条边对应相等的三角形.
不一定全等.
有两个条件对应相等也不能保证三角形全等.
结论
已知△ABC,画一个△DEF,使 DE=AB,EF=BC,DF=AC.
1.画线段DE=AB;
2.分别以D、E为圆心,线段AC、
BC为半径画弧,两弧交于点F;
3.连接线段DF、EF.
D
E
A
B
C
F
(1) 三角形的三条边分别对应相等的三角形?
3.三个条件.
判断两个三角形是否全等?
一个角对应相等
一条边对应相等
一个角,一条边分别对应相等
两条边对应相等
两个角对应相等
三个角对应相等
三条边对应相等
如果两个三角形的三边对应相等,那么这两个三角形全等. 可以简写成“边边边”或“SSS”.
基本事实一
文 字 符 号 图 形
三边对应 相等的两 个三角形 全等 在△ABC和△ DEF中 AB=DE BC=EF AC=DF ∴ △ABC ≌ △ DEF (SSS )
B
A
C
E
D
F
1.画∠B’ =∠B;
2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.
3.连接A’C’.
以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;
画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O 于点P;
以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;
过点Q画射线B’F,则∠OB’F =∠B
A
B
C
A’
B’
C’
M
N
O
P
Q
F
·
·
(三)当堂训练
赛前热身
(1)已知△ABC≌△DEF,那么_=_,_=_,_=_;_=_,_=_,_=_。
(2)在△ABC和△ DEF中
AB =_
_ = EF
_ = _
∴ △__≌△ __( )
B
A
C
E
D
F
3.8cm
5.3cm
6cm
40°
60°
80°
40°
⑴
40°
80°
⑷
3.8cm
6cm
5.3cm
⑶
6cm
80°
⑵
比 眼 力
如图,已知AB=AD,BE=DE,
△ABE与△ADE全等吗?
如何变换使两个三角形重合
A
B
D
E
比 速 度
1.如图,AB=CD, AC=BD,△ABC和△DCB是否全等?试说明理由。
如何变换使两个三角形重合
B
C
D
A
比 规 范
2.如图,点C,E,B,F在同一条
直线上,AB=DE,AC=DF,CE=BF,
请说明∠A=∠D的理由。
如何变换使两个三角形重合
A
C
E
D
F
B
1.△ABC中,BC=8,AB=6,AC=5
△DEF中,DE=6,EF=8,
要使 △ABC 与△DEF全等,则DF等于( )
A.8 B.6 C.10 D.5
比 反 应
B
A
C
E
D
F
2.如图,已知AB=AC,AD=AE,要说明∠BAD= ∠CAE,只需添加一个条件,添加的这个条件可以是 .
A
B
D
E
C
小明用四根木条,其中AB=AC,BD=CD,摆成如图所示的四边形.在上述条件不变的情况下,当他不断改变∠A的大小,使这个四边形的形状发生变化, ∠B与∠C的大小相等吗?为什么?
A
B
C
D
达标检测
(四)回忆总结,归纳提升
1.你今天学会了什么?
2.(生活中的数学)
瓦工师傅盖房时,看房梁是否平行,有时就用一块等腰三角形板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角形底边中心,房梁就是水平的,这是为什么?
A
B
D
C
比 收 获
1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)
2.边边边公理发现过程中用到的数学方法(包括画图、猜想、分析、归纳等.)
3.边边边公理在应用中用到的数学方法:
证明线段(或角)相等 转 化 证明线段(或角)所在的两个三角形全等.
两个三角形全等的注意点:
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
小结:
3. 有时需添辅助线(如:造公共边)
作业:
1.课时练:达标检测+提能训练(必做)
拓展创新(选做)
2.预习下一节
全等三角形的判定(一)
预习检测:
1、判断两个三角形全等至少需要_ 条件。
2、如图所示,在△ABD 和△ACD中,AB=AC,BD=CD,能利用SSS证明△ABD≌ △ACD吗?为什么
A
B
C
D
3、已知三边长度,以小组为单位画出三角形。
1.掌握 “SSS”判定两个三角形全等.
2.经历对应条件下两个三角形全等的探究过程,让学生体会分类的思想.
3.通过图形变换,培养学生观察——思考——总结的良好思维习惯.
4.核心素养目标:培养学生几何直观、数学抽象以及逻辑推理的核心素养。
学习目标
1. 准确找出两个三角形的对应边、对应角
2. 规范书写全等三角形的证明过程
边边边的发现过程及辨析
教学重点
教学难点
(一)创设情境,提出问题
教学过程
学校有两块三角形装饰板如下图,小明想知道这两块板是否全等(这两块板很重又固定在墙上),你能帮小明想个办法吗?
(二)讨论探究,解决问题
探究用较少的条件来说明两个三角形全等。
角、边
一个角对应相等
一条边对应相等
一个角,一条边分别对应相等
两条边对应相等
两个角对应相等
三个角对应相等
三条边对应相等
两角一边对应相等、两边一角对应相等
分类得出不同的情况
1.一个条件.
(1)有一条边对应相等的三角形?
不一定全等.
三角形全等的探究
判断两个三角形全等的推理过程,叫做证明三角形全等.
问题引导下在学习
(2)有一个角对应相等的三角形?
一个条件,并不能保证三角形全等.
不一定全等.
结论
不一定全等.
(1) 三角形的一个角和一条边对应相等的三角形?
2.两个条件.
(2)三角形的两条边对应相等的三角形.
不一定全等.
有两个条件对应相等也不能保证三角形全等.
结论
已知△ABC,画一个△DEF,使 DE=AB,EF=BC,DF=AC.
1.画线段DE=AB;
2.分别以D、E为圆心,线段AC、
BC为半径画弧,两弧交于点F;
3.连接线段DF、EF.
D
E
A
B
C
F
(1) 三角形的三条边分别对应相等的三角形?
3.三个条件.
判断两个三角形是否全等?
一个角对应相等
一条边对应相等
一个角,一条边分别对应相等
两条边对应相等
两个角对应相等
三个角对应相等
三条边对应相等
如果两个三角形的三边对应相等,那么这两个三角形全等. 可以简写成“边边边”或“SSS”.
基本事实一
文 字 符 号 图 形
三边对应 相等的两 个三角形 全等 在△ABC和△ DEF中 AB=DE BC=EF AC=DF ∴ △ABC ≌ △ DEF (SSS )
B
A
C
E
D
F
1.画∠B’ =∠B;
2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.
3.连接A’C’.
以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;
画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O 于点P;
以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;
过点Q画射线B’F,则∠OB’F =∠B
A
B
C
A’
B’
C’
M
N
O
P
Q
F
·
·
(三)当堂训练
赛前热身
(1)已知△ABC≌△DEF,那么_=_,_=_,_=_;_=_,_=_,_=_。
(2)在△ABC和△ DEF中
AB =_
_ = EF
_ = _
∴ △__≌△ __( )
B
A
C
E
D
F
3.8cm
5.3cm
6cm
40°
60°
80°
40°
⑴
40°
80°
⑷
3.8cm
6cm
5.3cm
⑶
6cm
80°
⑵
比 眼 力
如图,已知AB=AD,BE=DE,
△ABE与△ADE全等吗?
如何变换使两个三角形重合
A
B
D
E
比 速 度
1.如图,AB=CD, AC=BD,△ABC和△DCB是否全等?试说明理由。
如何变换使两个三角形重合
B
C
D
A
比 规 范
2.如图,点C,E,B,F在同一条
直线上,AB=DE,AC=DF,CE=BF,
请说明∠A=∠D的理由。
如何变换使两个三角形重合
A
C
E
D
F
B
1.△ABC中,BC=8,AB=6,AC=5
△DEF中,DE=6,EF=8,
要使 △ABC 与△DEF全等,则DF等于( )
A.8 B.6 C.10 D.5
比 反 应
B
A
C
E
D
F
2.如图,已知AB=AC,AD=AE,要说明∠BAD= ∠CAE,只需添加一个条件,添加的这个条件可以是 .
A
B
D
E
C
小明用四根木条,其中AB=AC,BD=CD,摆成如图所示的四边形.在上述条件不变的情况下,当他不断改变∠A的大小,使这个四边形的形状发生变化, ∠B与∠C的大小相等吗?为什么?
A
B
C
D
达标检测
(四)回忆总结,归纳提升
1.你今天学会了什么?
2.(生活中的数学)
瓦工师傅盖房时,看房梁是否平行,有时就用一块等腰三角形板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角形底边中心,房梁就是水平的,这是为什么?
A
B
D
C
比 收 获
1.边边边公理:有三边对应相等的两个三角形全等 简写成“边边边”(SSS)
2.边边边公理发现过程中用到的数学方法(包括画图、猜想、分析、归纳等.)
3.边边边公理在应用中用到的数学方法:
证明线段(或角)相等 转 化 证明线段(或角)所在的两个三角形全等.
两个三角形全等的注意点:
1. 说明两三角形全等所需的条件应按对应边的顺序书写.
2. 结论中所出现的边必须在所证明的两个三角形中.
小结:
3. 有时需添辅助线(如:造公共边)
作业:
1.课时练:达标检测+提能训练(必做)
拓展创新(选做)
2.预习下一节
