人教版数学八年级上册12.1.1全等三角形课件(16张)
文档属性
| 名称 | 人教版数学八年级上册12.1.1全等三角形课件(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 06:53:20 | ||
图片预览



文档简介
*
12.1全等三角形
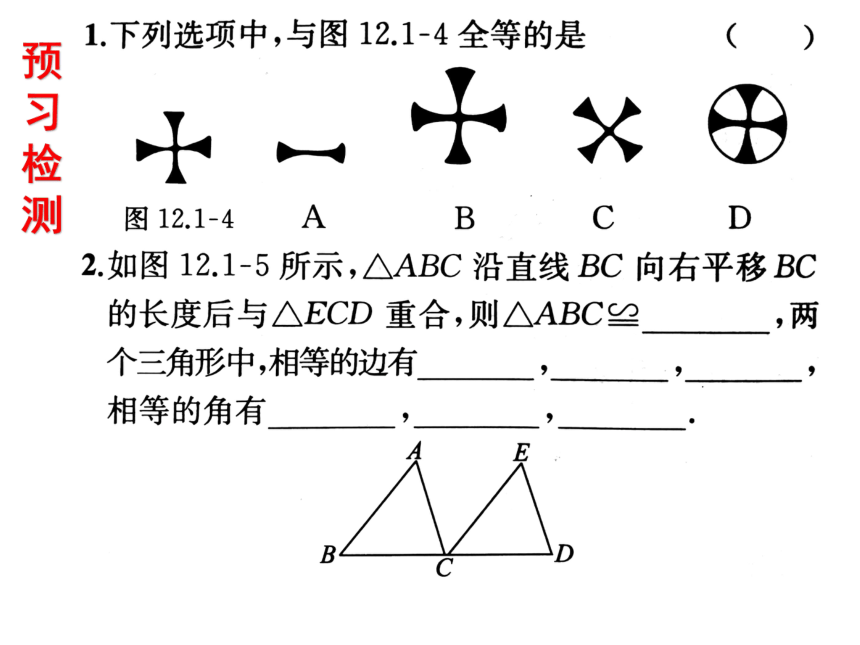
预习检测
教学目标
掌握全等形及全等三角形的相关概念。
会找全等三角形的对应顶点、对应角及对应边。
理解并掌握全等三角形的性质。
问题引导下的再学习
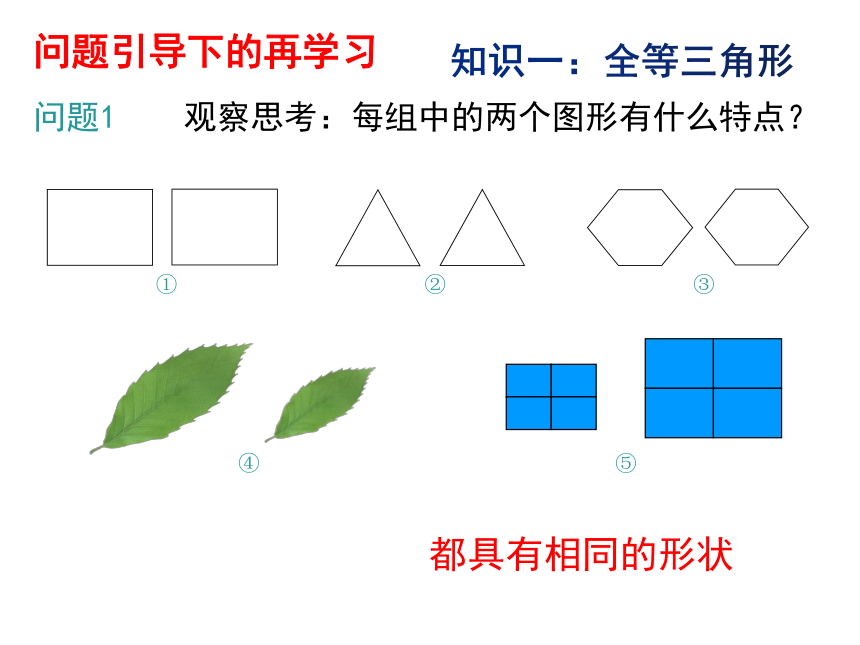
问题1 观察思考:每组中的两个图形有什么特点?
① ② ③
④
都具有相同的形状
⑤
归纳总结
全等形定义:
能够完全重合的两个图形叫做全等形.
全等形性质:
如果两个图形全等,它们的形状和大小一定都相等.
O
A
B
A
B
C
E
D
F
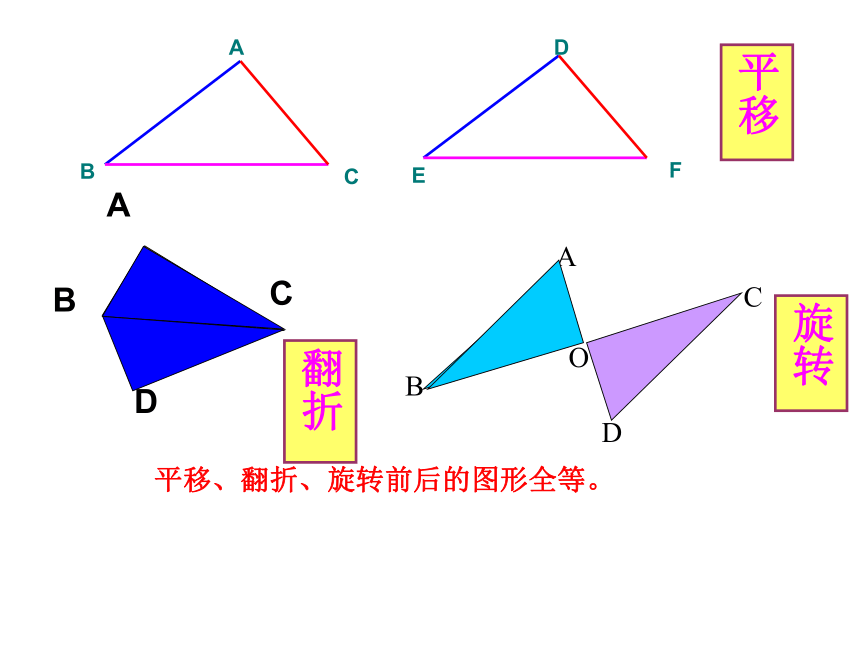
平移
翻折
D
C
A
B
C
D
旋转
平移、翻折、旋转前后的图形全等。
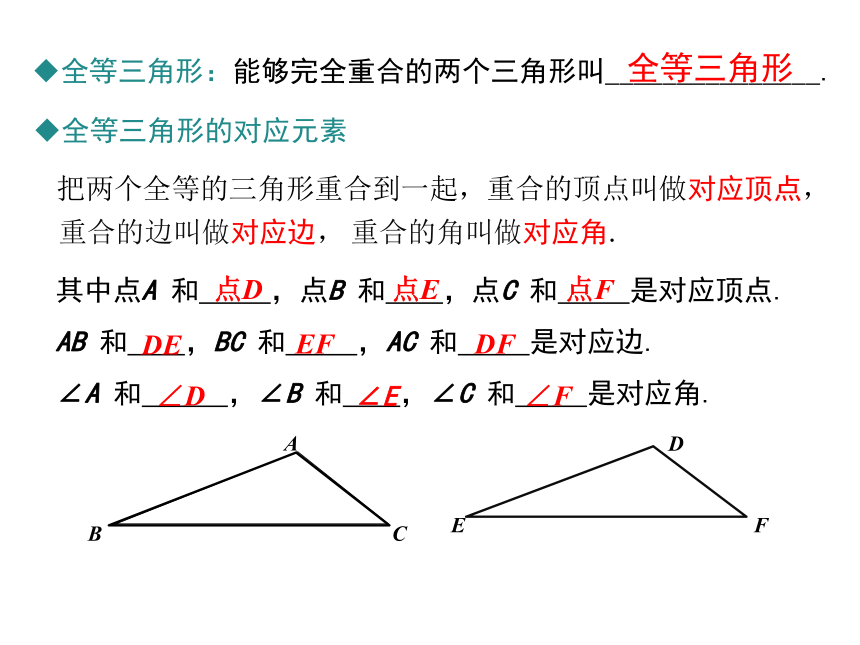
全等三角形:能够完全重合的两个三角形叫_______________.
全等三角形的对应元素
全等三角形
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
其中点A 和 ,点B 和 ,点C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
B
C
A
E
F
D
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
△ABC ≌ △FDE
A
B
C
E
D
F
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
如图: △ABC≌△DEF (已知)
∵
∴A B=D E,A C=D F,B C=EF(全等三角形对应边相等)
全等三角形的性质:
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形对应角相等)
注意:在表示全等三角形边、角相等时对应顶点写在对应位置上
全等三角形对应边相等;
全等三角形对应角相等.
问题引导下的再学习
1.判断题
①全等三角形的对应边相等,对应角相等。
②全等三角形的周长相等。
③周长相等的三角形是全等三角形。
④面积相等的三角形是全等三角形。
⑤全等三角形的面积相等。
当堂训练
√
√
×
×
√
当堂训练
当堂训练
3.如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
1.如图,△ABC≌△BAD,如果AB=5cm, BD= 4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm C.4cm D.无法确定
2.在上题中,∠CAB的对应角是( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
达标检测
达标检测
1.如图,△ABC≌△DEC,∠ACD=28°。求证:∠BCE=28°
证明:∵△ABC≌△DEC(已知)
∴∠ACB=∠ ( )
即∠ +∠DCB=∠ +∠DCB
∴∠_ =∠ _
又∵∠ACD=28°
∴∠ =28°
3.如图△ABC ≌ △DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并说明理由.
C
D
A
B
E
F
1
2
解:AC∥DF,BC∥EF.
理由:∵△ABC ≌△DEF,
∴∠A=∠2,∠1=∠E,
(全等三角形对应角相等).
∴AC∥DF,BC∥EF.
达标检测
12.1全等三角形
预习检测
教学目标
掌握全等形及全等三角形的相关概念。
会找全等三角形的对应顶点、对应角及对应边。
理解并掌握全等三角形的性质。
问题引导下的再学习
问题1 观察思考:每组中的两个图形有什么特点?
① ② ③
④
都具有相同的形状
⑤
归纳总结
全等形定义:
能够完全重合的两个图形叫做全等形.
全等形性质:
如果两个图形全等,它们的形状和大小一定都相等.
O
A
B
A
B
C
E
D
F
平移
翻折
D
C
A
B
C
D
旋转
平移、翻折、旋转前后的图形全等。
全等三角形:能够完全重合的两个三角形叫_______________.
全等三角形的对应元素
全等三角形
把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,
重合的角叫做对应角.
重合的边叫做对应边,
其中点A 和 ,点B 和 ,点C 和 是对应顶点.
AB 和 ,BC 和 ,AC 和 是对应边.
∠A 和 ,∠B 和 ,∠C 和 是对应角.
B
C
A
E
F
D
点D
点E
点F
DE
EF
DF
∠D
∠E
∠F
△ABC ≌ △FDE
A
B
C
E
D
F
全等的表示方法
“全等”用符号“≌”表示,读作“全等于”.
如图: △ABC≌△DEF (已知)
∵
∴A B=D E,A C=D F,B C=EF(全等三角形对应边相等)
全等三角形的性质:
∠A=∠D,∠B=∠E,∠C=∠F(全等三角形对应角相等)
注意:在表示全等三角形边、角相等时对应顶点写在对应位置上
全等三角形对应边相等;
全等三角形对应角相等.
问题引导下的再学习
1.判断题
①全等三角形的对应边相等,对应角相等。
②全等三角形的周长相等。
③周长相等的三角形是全等三角形。
④面积相等的三角形是全等三角形。
⑤全等三角形的面积相等。
当堂训练
√
√
×
×
√
当堂训练
当堂训练
3.如图,△ABC≌△DEF,∠A=70°,∠B=50°,BF=4,EF=7,求∠DEF的度数和CF的长.
解:∵△ABC≌△DEF,∠A=70°,
∠B=50°,BF=4,EF=7,
∴∠DEF=∠B=50°,BC=EF=7,
∴CF=BC-BF=7-4=3.
1.如图,△ABC≌△BAD,如果AB=5cm, BD= 4cm,AD=6cm,那么BC的长是( )
A.6cm B.5cm C.4cm D.无法确定
2.在上题中,∠CAB的对应角是( )
A.∠DAB B.∠DBA C.∠DBC D.∠CAD
A
O
C
D
B
A
B
达标检测
达标检测
1.如图,△ABC≌△DEC,∠ACD=28°。求证:∠BCE=28°
证明:∵△ABC≌△DEC(已知)
∴∠ACB=∠ ( )
即∠ +∠DCB=∠ +∠DCB
∴∠_ =∠ _
又∵∠ACD=28°
∴∠ =28°
3.如图△ABC ≌ △DEF,边AB和DE在同一条直线上,试说明图中有哪些线段平行,并说明理由.
C
D
A
B
E
F
1
2
解:AC∥DF,BC∥EF.
理由:∵△ABC ≌△DEF,
∴∠A=∠2,∠1=∠E,
(全等三角形对应角相等).
∴AC∥DF,BC∥EF.
达标检测
