五年级下册数学讲义-第六章 圆的周长和面积 无答案 苏教版
文档属性
| 名称 | 五年级下册数学讲义-第六章 圆的周长和面积 无答案 苏教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 00:00:00 | ||
图片预览




文档简介
数学五年级下册第六章 圆的周长和面积
学员编号:*********** 年 级:小五 课 时 数: 3
学员姓名:**** 辅导科目:数学 学科教师: ****
授课目标
了解认识圆的周长和面积计算方式
授课难点
学会圆的周长和面积计算方式
教学重点:圆的周长和面积计算方式
1圆面积推导:圆可以切拼成近似的长方形,长方形的面积与圆的面积相等;长方形的宽是圆的半径;长方形的长是圆周长的一半。因为长方形的面积=长×宽,所以圆的面积=圆周长的一半×半径,S圆=πr×r=πr2
2圆的面积公式:圆的面积=半径的平方×圆周率,S圆=πr2。
半圆的面积是圆面积的一半。S半圆=πr2÷2
3大小两个圆比较:半径的倍数=直径的倍数=周长的倍数,面积的倍数=半径的倍数平方
4、环形的面积如何计算?S圆环= p×(false外-false内)
141605657860解题锦囊
解题锦囊
求圆的面积,先要求出这个圆的半径,再根据圆的面积公式进行计算。
填表。(r、d、C的单位:厘米 S的单位:平方厘米)
半径(r)
2
直径(d)
7
10
周长(C)
15.7
面积(S)
选择。
右图中阴影部分的面积和半圆的面积相比( )。
阴影部分的面积大
半圆的面积大
阴影部分的面积和半圆的面积相等
不能确定
一个圆形铁通盖的直径是30厘米,做这个铁通至少需要多少平方厘米的铁皮?
一种炸弹的有效杀伤半径是20米,它的有效杀伤面积多少平方米?
用一根长为21.98分米的铁丝围一个圆,这个圆的面积是多少平方分米?
计算阴影部分的面积。(单位:厘米)
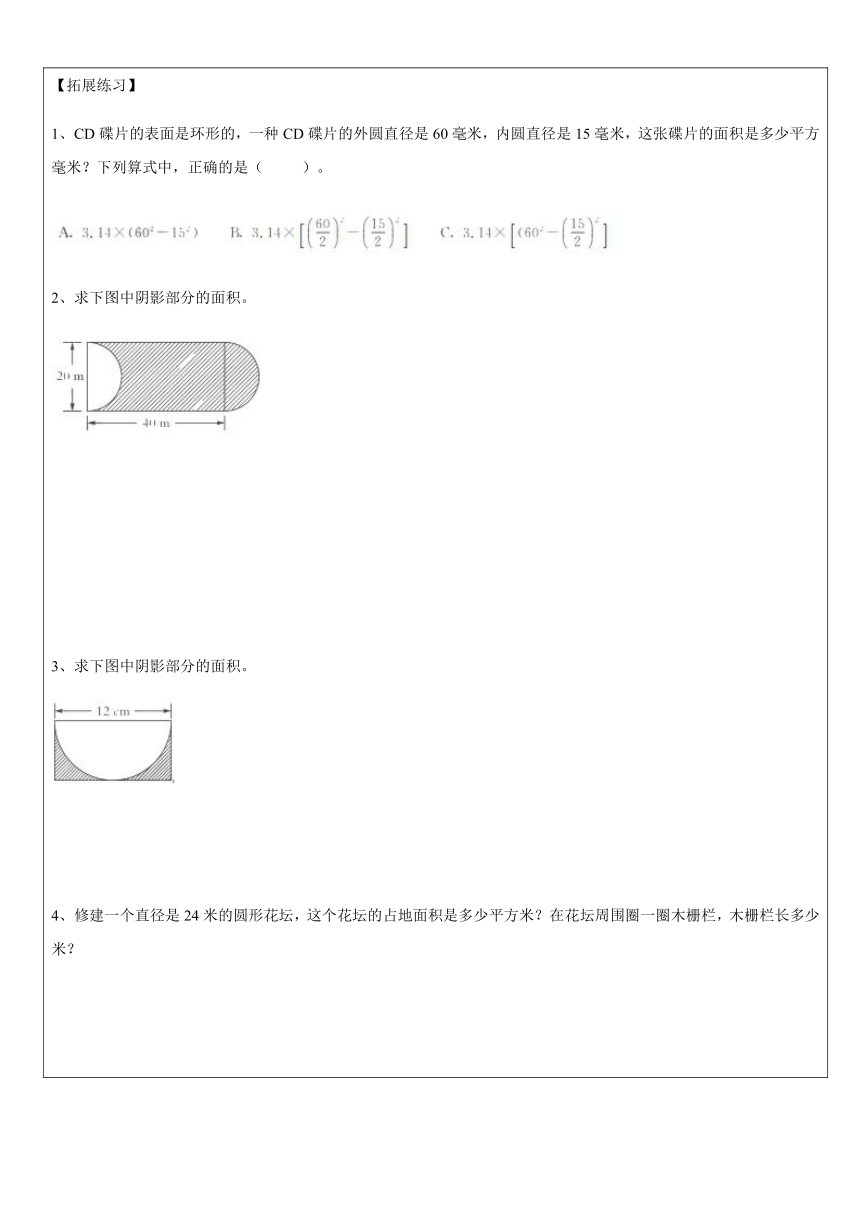
【拓展练习】
CD碟片的表面是环形的,一种CD碟片的外圆直径是60毫米,内圆直径是15毫米,这张碟片的面积是多少平方毫米?下列算式中,正确的是( )。
求下图中阴影部分的面积。
求下图中阴影部分的面积。
修建一个直径是24米的圆形花坛,这个花坛的占地面积是多少平方米?在花坛周围圈一圈木栅栏,木栅栏长多少米?
把圆分成若干等份后,再拼成一个近似的长方形(如下图),这时周长增加了20厘米。这个圆的面积是多少平方厘米?
下图中长方形ABCD的面积是6平方厘米,圆的面积是多少平方厘米?
【综合练习1】
求右图中阴影部分的面积。(单位:分米)
2、求下图中阴影部分的面积。
3、下图中圆的周长是12.56米,圆的面积和长方形的面积相等,长方形的长是多少米?
4、求下图中阴影部分的面积。
【综合练习2】
画一个半径为1厘米的圆,用字母标出它的圆心、半径和直径。
一个圆形铁片的直径是1.8分米,它的周长是多少分米?面积是多少平方分米?
一棵大树根部树干(近似于圆)的周长是47.1分米。
这棵大树根部树干的半径大约是多少分米?
这棵大树根部树干的横截面的面积大约是多少平方分米?
4、一个环形的外圆半径是8分米,内圆半径是5分米,这个环形的面积是多少平方米?
例1、如图,四根直径相同的管子被一根金属带仅仅地捆在一起,已知阴影部分的面积是0.615平方米,试问:金属带的长度是多少米?
【做一做】有七根直径2分米的圆柱形木棍,想用一根绳子把它们捆成一捆,问:最短需要多少分米长的绳子?
例2:用两根都是6.28米长的铁丝,分别围成一个正方形和一个圆,问:哪一个的面积大?大多少?
【做一做】用两根长都是12.56厘米的铁丝,分别围成一个正方形和一个圆,问:哪一个的面积大?大多少?
例3:如图,三角形S1的面积是24平方厘米,斜边长10厘米。将它以O点为中心旋转90°,问:三角形扫过的面积是多少?(false)
【做一做】如图,是一个直径为3厘米的半圆,AB是直径。设A点不动,把整个半圆逆时针旋转60°,此时B点异动都C点(见图),那么图中阴影部分的面积是多少?
例4、如图,一个圆心角是45°的扇形,其中等腰直角三角形的直角边是6厘米,问:阴影部分的面积是多少?
【做一做】计算如图阴影部分的面积是多少?(单位:厘米)
例5:如图:falseBOA=90°,若以OA为直径画半圆OD于K,且falseAOD=45°,又图中的面积为1平方厘米,求阴影部分的面积。
【做一做】如图,阴影部分的面积比阴影部分的面积大28平方厘米,直径AB长40厘米,求BC的长是多少?
例6:草场上有一个长20米,宽10米的关闭着的羊圈,在圈的一角用长30米的绳子拴着一只羊(见左下图)问:这只羊能够活动的范围有多大?
【做一做】有一只狗被拴在一个边长为3米的等边三角形建筑物的墙角上(见下图),绳长是4米,求狗所能到达的总面积。
二、专题过关
1、如图所示,已知大圆O的半径为20厘米,求a,b,c,d四个小圆的周长之和。
2、如图1,图2所示,求阴影部分的面积(单位:厘米)
3、如图所示,已知△OAB为等腰直角三角形,面积为20平方厘米,求阴影部分的面积。
4、如图所示,已知长方形ABCD中,CD长为10厘米,BC长为6厘米,DCE为扇形,求两块阴影部分的面积之差。
5、如图所示,已知正方形边长为20厘米,求阴影部分的面积。
6、如图所示大圆半径为6,求阴影部分的面积。
7、已知正方形ABCD的边长为10厘米,过它的四个定点作一个大圆,过它的各边重点作一个小圆,再将边中点用直线连接起来,得到下图,那么,图中阴影部分的面积是多少?
8、如图所示,正方形ABCD的面积为200平方厘米,求内切圆的面积。(false取3.14)
9、如图所示,已知圆的面积为3140拼房厘米,求内接正方形ABCD的面积。(false取3.14)
10、如图所示,已知大正方形的面积为100平方厘米,小正方形的面积为50平方厘米,求阴影部分的面积。
1、专题特点:本专题研究圆与各种图形的组合图形。一般的组合图形都是由一些基本图形拼合或重叠而成的。
2、解题方法:确定弧的长度,弧所对的圆心角大小。
圆心角分别是60°、90°、120°、270°,false的扇形可以看做是false的圆来计算面积。
3、注意事项:在涉及圆的面积计算中,有很多时候要用代换法,我们不能直接求出r是多少,但是我们可以知道r2是多少。
例1、两条爬行速度相同的小虫同时从起点出发,分别沿A、B两条跑道爬行(如图),其起点部分与终点部分都是直道,中间绕过的是半圆形跑道。如果跑道每道宽1.22米,要使它们同时到达各自的终点,跑道B的终点与跑道A的终点相距多少米?
【做一做】赤道是地球的“腰带”,它长约4万千米。如果这条想象的“长带”离开地球表面2米,那么,它会比原来长出多少米?
例2:如图所示,如果四个等圆的半径为1厘米,求(1)阴影部分的总面积。(2)四个圆盖住的总面积。
【做一做】求如图中的阴影部分与大圆的面积之比和周长之比。
例3:如图,其中圆的周长等于正三角形的一条边的边长,该圆绕着三角形外周滚动一周,问:圆自转了多少圈?
【做一做】桌上放着大小一样的两枚硬币,其中一枚硬币固定不动,另一枚硬币沿着定币的外缘做无滑动的滚动,当动币绕着定币滚动一周后,动币自转了几圈?
例4、如图所示,一个圆在正五角星形的外侧,从A处开始做与正五角星形的边相切(即紧靠边)的滚动。如果BC长度等于圆周长,问:当此圆滚动回到原出发点时(包括自转)共转了几圈?
【做一做】如图,若一个圆的周长等于一个正方形的边长,将此圆绕着正方形外侧滚动一周,则圆转动了几圈?
例5:如图,在一个大正方形里有一个小正方形ABCD,小正方形沿大正方形的边翻转,翻转两次后,求顶点B所划过的曲线的长度,并画出这一曲线(大正方形的边长为2厘米,小正方形的边长为1厘米)
【做一做】有一边长为1的等边三角形,现将三角形沿水平线翻动,如下图所示,B点从开始的位置到结束的位置,它所经过的路线总长度是多少?
例6:如图,大轮B是个定轮,小轮A沿B轮的外沿滚动。问:
图(1)中,若小轮A公转一周所扫过的面积是301.44平方厘米,则小轮A的半径是多少?
图(2)中,小轮的圆心A所划出的图形是什么曲线?周长是多少?(你可以用硬币进行试验)
【做一做】有一个边长为1厘米的等边三角形,现将三角形沿水平线翻动,如果这个三角形的面积近似为0.87平方厘米,求三角形运动时所扫过的面积。
1、专题特点:本专题研究圆与各种图形的组合图形。一般的组合图形都是由一些基本图形拼合或重叠而成的。
2、解题方法:确定弧的长度,弧所对的圆心角大小。
圆心角分别是60°、90°、120°、270°,false的扇形可以看做是false的圆来计算面积。
注意事项:(1)圆上任意一点到圆心的距离都相等。
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴。
圆周率是一个无限不循环小数,圆周率是圆周长C与直径d的比值:false。
圆的面积falser2,这一公式的得来是用等分圆周逼近法求出来的。
扇形是圆的一部分,圆心角为n度的扇形面积公式为S扇形=false。先把圆周false分成360份,每份长false,所以圆心角为n度的扇形的弧长为弧AB=falsefalsen=false
学员编号:*********** 年 级:小五 课 时 数: 3
学员姓名:**** 辅导科目:数学 学科教师: ****
授课目标
了解认识圆的周长和面积计算方式
授课难点
学会圆的周长和面积计算方式
教学重点:圆的周长和面积计算方式
1圆面积推导:圆可以切拼成近似的长方形,长方形的面积与圆的面积相等;长方形的宽是圆的半径;长方形的长是圆周长的一半。因为长方形的面积=长×宽,所以圆的面积=圆周长的一半×半径,S圆=πr×r=πr2
2圆的面积公式:圆的面积=半径的平方×圆周率,S圆=πr2。
半圆的面积是圆面积的一半。S半圆=πr2÷2
3大小两个圆比较:半径的倍数=直径的倍数=周长的倍数,面积的倍数=半径的倍数平方
4、环形的面积如何计算?S圆环= p×(false外-false内)
141605657860解题锦囊
解题锦囊
求圆的面积,先要求出这个圆的半径,再根据圆的面积公式进行计算。
填表。(r、d、C的单位:厘米 S的单位:平方厘米)
半径(r)
2
直径(d)
7
10
周长(C)
15.7
面积(S)
选择。
右图中阴影部分的面积和半圆的面积相比( )。
阴影部分的面积大
半圆的面积大
阴影部分的面积和半圆的面积相等
不能确定
一个圆形铁通盖的直径是30厘米,做这个铁通至少需要多少平方厘米的铁皮?
一种炸弹的有效杀伤半径是20米,它的有效杀伤面积多少平方米?
用一根长为21.98分米的铁丝围一个圆,这个圆的面积是多少平方分米?
计算阴影部分的面积。(单位:厘米)
【拓展练习】
CD碟片的表面是环形的,一种CD碟片的外圆直径是60毫米,内圆直径是15毫米,这张碟片的面积是多少平方毫米?下列算式中,正确的是( )。
求下图中阴影部分的面积。
求下图中阴影部分的面积。
修建一个直径是24米的圆形花坛,这个花坛的占地面积是多少平方米?在花坛周围圈一圈木栅栏,木栅栏长多少米?
把圆分成若干等份后,再拼成一个近似的长方形(如下图),这时周长增加了20厘米。这个圆的面积是多少平方厘米?
下图中长方形ABCD的面积是6平方厘米,圆的面积是多少平方厘米?
【综合练习1】
求右图中阴影部分的面积。(单位:分米)
2、求下图中阴影部分的面积。
3、下图中圆的周长是12.56米,圆的面积和长方形的面积相等,长方形的长是多少米?
4、求下图中阴影部分的面积。
【综合练习2】
画一个半径为1厘米的圆,用字母标出它的圆心、半径和直径。
一个圆形铁片的直径是1.8分米,它的周长是多少分米?面积是多少平方分米?
一棵大树根部树干(近似于圆)的周长是47.1分米。
这棵大树根部树干的半径大约是多少分米?
这棵大树根部树干的横截面的面积大约是多少平方分米?
4、一个环形的外圆半径是8分米,内圆半径是5分米,这个环形的面积是多少平方米?
例1、如图,四根直径相同的管子被一根金属带仅仅地捆在一起,已知阴影部分的面积是0.615平方米,试问:金属带的长度是多少米?
【做一做】有七根直径2分米的圆柱形木棍,想用一根绳子把它们捆成一捆,问:最短需要多少分米长的绳子?
例2:用两根都是6.28米长的铁丝,分别围成一个正方形和一个圆,问:哪一个的面积大?大多少?
【做一做】用两根长都是12.56厘米的铁丝,分别围成一个正方形和一个圆,问:哪一个的面积大?大多少?
例3:如图,三角形S1的面积是24平方厘米,斜边长10厘米。将它以O点为中心旋转90°,问:三角形扫过的面积是多少?(false)
【做一做】如图,是一个直径为3厘米的半圆,AB是直径。设A点不动,把整个半圆逆时针旋转60°,此时B点异动都C点(见图),那么图中阴影部分的面积是多少?
例4、如图,一个圆心角是45°的扇形,其中等腰直角三角形的直角边是6厘米,问:阴影部分的面积是多少?
【做一做】计算如图阴影部分的面积是多少?(单位:厘米)
例5:如图:falseBOA=90°,若以OA为直径画半圆OD于K,且falseAOD=45°,又图中的面积为1平方厘米,求阴影部分的面积。
【做一做】如图,阴影部分的面积比阴影部分的面积大28平方厘米,直径AB长40厘米,求BC的长是多少?
例6:草场上有一个长20米,宽10米的关闭着的羊圈,在圈的一角用长30米的绳子拴着一只羊(见左下图)问:这只羊能够活动的范围有多大?
【做一做】有一只狗被拴在一个边长为3米的等边三角形建筑物的墙角上(见下图),绳长是4米,求狗所能到达的总面积。
二、专题过关
1、如图所示,已知大圆O的半径为20厘米,求a,b,c,d四个小圆的周长之和。
2、如图1,图2所示,求阴影部分的面积(单位:厘米)
3、如图所示,已知△OAB为等腰直角三角形,面积为20平方厘米,求阴影部分的面积。
4、如图所示,已知长方形ABCD中,CD长为10厘米,BC长为6厘米,DCE为扇形,求两块阴影部分的面积之差。
5、如图所示,已知正方形边长为20厘米,求阴影部分的面积。
6、如图所示大圆半径为6,求阴影部分的面积。
7、已知正方形ABCD的边长为10厘米,过它的四个定点作一个大圆,过它的各边重点作一个小圆,再将边中点用直线连接起来,得到下图,那么,图中阴影部分的面积是多少?
8、如图所示,正方形ABCD的面积为200平方厘米,求内切圆的面积。(false取3.14)
9、如图所示,已知圆的面积为3140拼房厘米,求内接正方形ABCD的面积。(false取3.14)
10、如图所示,已知大正方形的面积为100平方厘米,小正方形的面积为50平方厘米,求阴影部分的面积。
1、专题特点:本专题研究圆与各种图形的组合图形。一般的组合图形都是由一些基本图形拼合或重叠而成的。
2、解题方法:确定弧的长度,弧所对的圆心角大小。
圆心角分别是60°、90°、120°、270°,false的扇形可以看做是false的圆来计算面积。
3、注意事项:在涉及圆的面积计算中,有很多时候要用代换法,我们不能直接求出r是多少,但是我们可以知道r2是多少。
例1、两条爬行速度相同的小虫同时从起点出发,分别沿A、B两条跑道爬行(如图),其起点部分与终点部分都是直道,中间绕过的是半圆形跑道。如果跑道每道宽1.22米,要使它们同时到达各自的终点,跑道B的终点与跑道A的终点相距多少米?
【做一做】赤道是地球的“腰带”,它长约4万千米。如果这条想象的“长带”离开地球表面2米,那么,它会比原来长出多少米?
例2:如图所示,如果四个等圆的半径为1厘米,求(1)阴影部分的总面积。(2)四个圆盖住的总面积。
【做一做】求如图中的阴影部分与大圆的面积之比和周长之比。
例3:如图,其中圆的周长等于正三角形的一条边的边长,该圆绕着三角形外周滚动一周,问:圆自转了多少圈?
【做一做】桌上放着大小一样的两枚硬币,其中一枚硬币固定不动,另一枚硬币沿着定币的外缘做无滑动的滚动,当动币绕着定币滚动一周后,动币自转了几圈?
例4、如图所示,一个圆在正五角星形的外侧,从A处开始做与正五角星形的边相切(即紧靠边)的滚动。如果BC长度等于圆周长,问:当此圆滚动回到原出发点时(包括自转)共转了几圈?
【做一做】如图,若一个圆的周长等于一个正方形的边长,将此圆绕着正方形外侧滚动一周,则圆转动了几圈?
例5:如图,在一个大正方形里有一个小正方形ABCD,小正方形沿大正方形的边翻转,翻转两次后,求顶点B所划过的曲线的长度,并画出这一曲线(大正方形的边长为2厘米,小正方形的边长为1厘米)
【做一做】有一边长为1的等边三角形,现将三角形沿水平线翻动,如下图所示,B点从开始的位置到结束的位置,它所经过的路线总长度是多少?
例6:如图,大轮B是个定轮,小轮A沿B轮的外沿滚动。问:
图(1)中,若小轮A公转一周所扫过的面积是301.44平方厘米,则小轮A的半径是多少?
图(2)中,小轮的圆心A所划出的图形是什么曲线?周长是多少?(你可以用硬币进行试验)
【做一做】有一个边长为1厘米的等边三角形,现将三角形沿水平线翻动,如果这个三角形的面积近似为0.87平方厘米,求三角形运动时所扫过的面积。
1、专题特点:本专题研究圆与各种图形的组合图形。一般的组合图形都是由一些基本图形拼合或重叠而成的。
2、解题方法:确定弧的长度,弧所对的圆心角大小。
圆心角分别是60°、90°、120°、270°,false的扇形可以看做是false的圆来计算面积。
注意事项:(1)圆上任意一点到圆心的距离都相等。
圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴。
圆周率是一个无限不循环小数,圆周率是圆周长C与直径d的比值:false。
圆的面积falser2,这一公式的得来是用等分圆周逼近法求出来的。
扇形是圆的一部分,圆心角为n度的扇形面积公式为S扇形=false。先把圆周false分成360份,每份长false,所以圆心角为n度的扇形的弧长为弧AB=falsefalsen=false
