第五章 相交线与平行线 平行线及其判定 平行线的判定
文档属性
| 名称 | 第五章 相交线与平行线 平行线及其判定 平行线的判定 |
|
|
| 格式 | rar | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-06 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
5.2.2 平行线的判定
学习目标
1、进一步理解同位角、内错角、同旁内角的概念及识别方法;
2、掌握利用同位角相等、内错角相等及同旁内角互补判定两条直线平行的方法。
知识回顾:
1、什么叫同位角?内错角?怎样的两个角是同旁内角?
2、判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁)。
(1)平行线的定义;
(2)平行公理的推论。
变式练习:
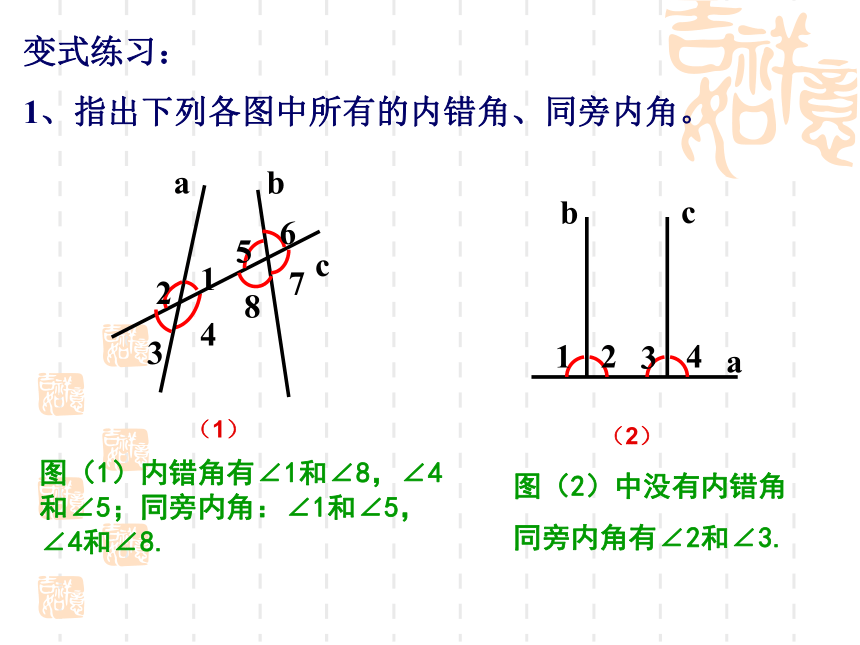
1、指出下列各图中所有的内错角、同旁内角。
b
c
a
1
4
3
2
a
b
c
8
4
3
2
1
7
6
5
图(1)内错角有∠1和∠8,∠4和∠5;同旁内角:∠1和∠5,∠4和∠8.
图(2)中没有内错角
同旁内角有∠2和∠3.
(1)
(2)
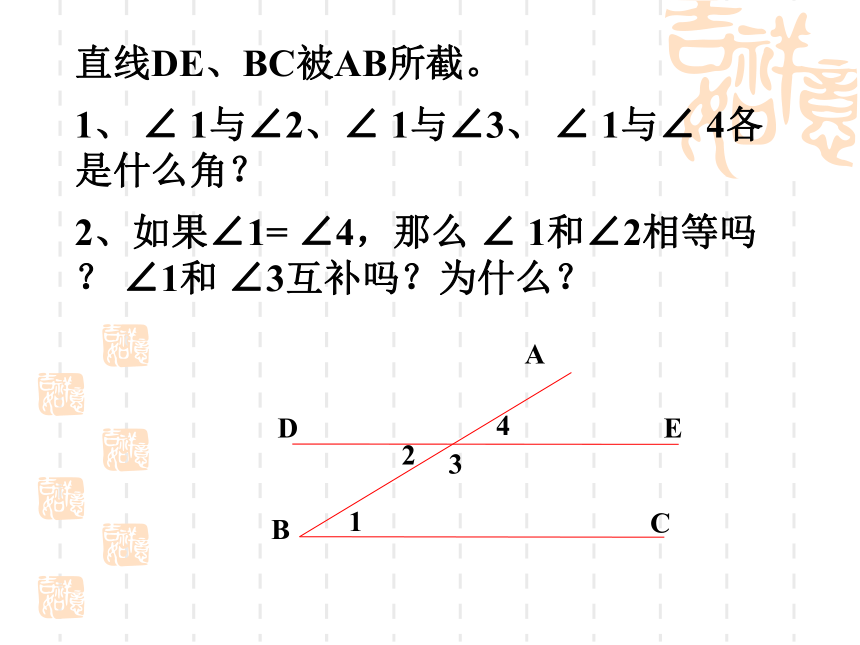
直线DE、BC被AB所截。
1、 ∠ 1与∠2、∠ 1与∠3、 ∠ 1与∠ 4各是什么角?
2、如果∠1= ∠4,那么 ∠ 1和∠2相等吗? ∠1和 ∠3互补吗?为什么?
D
E
A
B
C
1
2
3
4
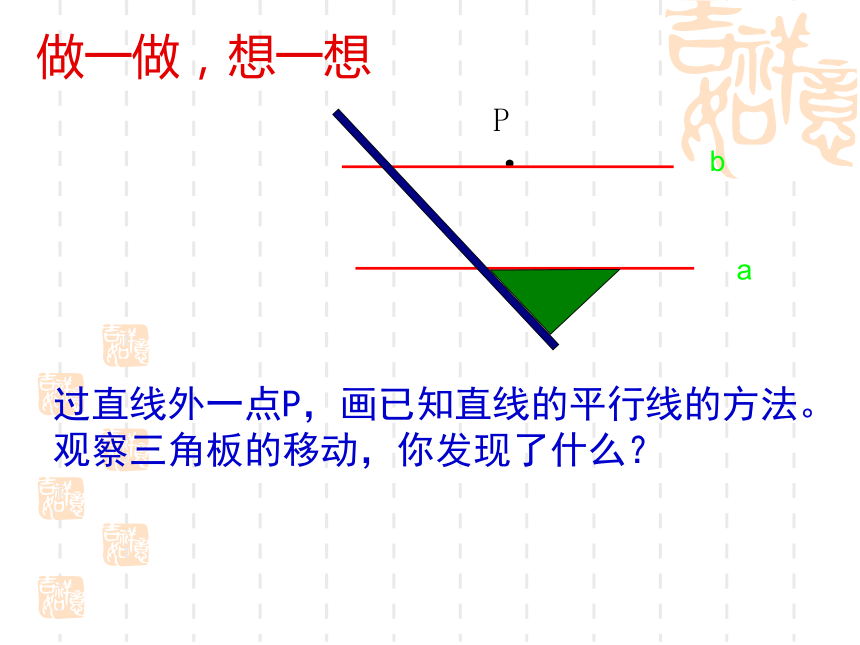
做一做,想一想
P
·
过直线外一点P,画已知直线的平行线的方法。观察三角板的移动,你发现了什么?
a
b
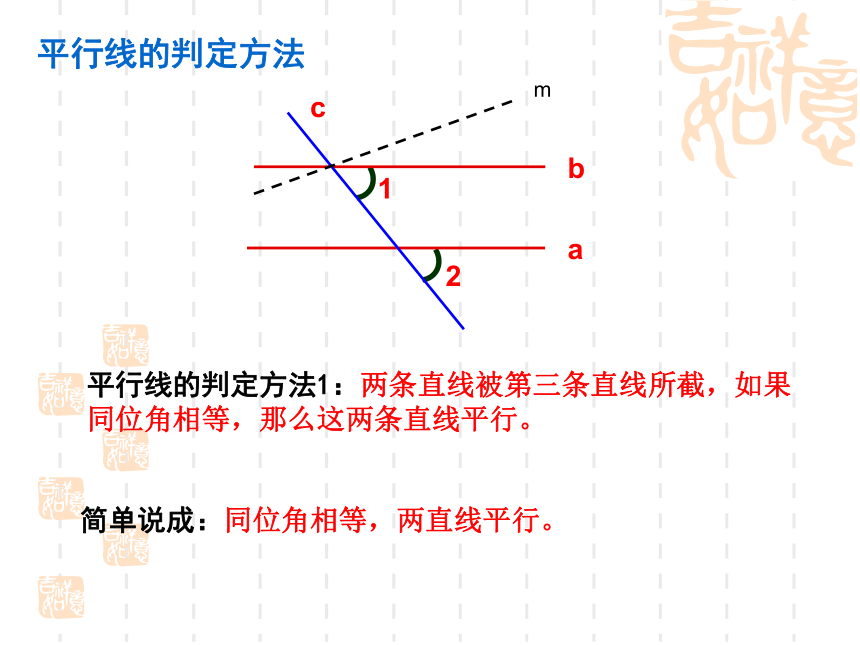
平行线的判定方法
1
2
a
b
c
m
平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
已知:∠1=450 ,∠ 2=1350, l1∥l2吗?
想一想
3
4
思考:1、∠2与∠4有什么关系?l1∥l2吗?
2、∠3与∠4有什么关系?l1∥l2吗?
由此,我们得到了平行线的第二、三种判定方法:
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
1、如图,由 可判断哪两条直线平行?由 ,可判断哪两条直线平行?
跟踪练习:
2、在下列结论给出的条件中,不能判定AB∥DF ( )
A、∠A+ ∠2=1800
B、∠A=∠3
C、∠1=∠4
D、∠1=∠A
A
E
B
D
C
F
1
4
2
3
D
2
1
讲一讲
例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
练一练:
1、课后练习;
2、补充练习:如图,已知点C在射线BD上, ∠ ACE= ∠ A,试从给出的条件出发,结合图形,写出尽可能多的结论。
B
A
C
D
E
A
B
F
C
D
E
已知∠BAF=500, ∠ACE=1400,CD⊥CE,则有DC∥AB,试说明理由
500
1400
可以采用多种思路说明
小 结
1、这节课研究的是平行线的判定方法。学生口述
平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
反馈练习:
一、选择题:(每小题3分,共15分)
1.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
2.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
4.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
5.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
5.2.2 平行线的判定
学习目标
1、进一步理解同位角、内错角、同旁内角的概念及识别方法;
2、掌握利用同位角相等、内错角相等及同旁内角互补判定两条直线平行的方法。
知识回顾:
1、什么叫同位角?内错角?怎样的两个角是同旁内角?
2、判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁)。
(1)平行线的定义;
(2)平行公理的推论。
变式练习:
1、指出下列各图中所有的内错角、同旁内角。
b
c
a
1
4
3
2
a
b
c
8
4
3
2
1
7
6
5
图(1)内错角有∠1和∠8,∠4和∠5;同旁内角:∠1和∠5,∠4和∠8.
图(2)中没有内错角
同旁内角有∠2和∠3.
(1)
(2)
直线DE、BC被AB所截。
1、 ∠ 1与∠2、∠ 1与∠3、 ∠ 1与∠ 4各是什么角?
2、如果∠1= ∠4,那么 ∠ 1和∠2相等吗? ∠1和 ∠3互补吗?为什么?
D
E
A
B
C
1
2
3
4
做一做,想一想
P
·
过直线外一点P,画已知直线的平行线的方法。观察三角板的移动,你发现了什么?
a
b
平行线的判定方法
1
2
a
b
c
m
平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
已知:∠1=450 ,∠ 2=1350, l1∥l2吗?
想一想
3
4
思考:1、∠2与∠4有什么关系?l1∥l2吗?
2、∠3与∠4有什么关系?l1∥l2吗?
由此,我们得到了平行线的第二、三种判定方法:
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
1、如图,由 可判断哪两条直线平行?由 ,可判断哪两条直线平行?
跟踪练习:
2、在下列结论给出的条件中,不能判定AB∥DF ( )
A、∠A+ ∠2=1800
B、∠A=∠3
C、∠1=∠4
D、∠1=∠A
A
E
B
D
C
F
1
4
2
3
D
2
1
讲一讲
例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
练一练:
1、课后练习;
2、补充练习:如图,已知点C在射线BD上, ∠ ACE= ∠ A,试从给出的条件出发,结合图形,写出尽可能多的结论。
B
A
C
D
E
A
B
F
C
D
E
已知∠BAF=500, ∠ACE=1400,CD⊥CE,则有DC∥AB,试说明理由
500
1400
可以采用多种思路说明
小 结
1、这节课研究的是平行线的判定方法。学生口述
平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简单说成:同位角相等,两直线平行。
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简单说成:内错角相等,两直线平行。
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简单说成:同旁内角互补,两直线平行。
反馈练习:
一、选择题:(每小题3分,共15分)
1.如图1所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD=∠BCD B.∠1=∠2; C.∠3=∠4 D.∠BAC=∠ACD
(1) (2)
2.如图2所示,如果∠D=∠EFC,那么( )
A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF
3.如图3所示,能判断AB∥CE的条件是( )
A.∠A=∠ACE B.∠A=∠ECD C.∠B=∠BCA D.∠B=∠ACE
(3)
4.下列说法错误的是( )
A.同位角不一定相等 B.内错角都相等
C.同旁内角可能相等 D.同旁内角互补,两直线平行
5.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( )
A.平行 B.垂直 C.平行或垂直 D.平行或垂直或相交
