2019-2020学年湖北省宜昌市天问高中高二下学期开学数学试卷 (Word解析版)
文档属性
| 名称 | 2019-2020学年湖北省宜昌市天问高中高二下学期开学数学试卷 (Word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 00:00:00 | ||
图片预览



文档简介
2019-2020学年湖北宜昌市天问高中高二第二学期开学数学试卷
一、选择题(共12小题).
1.设随机变量ξ服从正态分布N(1,σ2),若P(ξ<2)=0.8,则P(0<ξ<1)的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
2.已知=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),若P,A,B,C四点共面,则λ=( )
A.9 B.﹣9 C.﹣3 D.3
3.设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),且⊥,∥,则|+|=( )
A. B. C.3 D.4
4.已知空间向量,,且,则向量与(λ≠0)的夹角为( )
A. B.或 C. D.或
5.如图,在平行六面体ABCD﹣A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
A. B. C. D.
6.在正四面体P﹣ABC中,棱长为2,且E是棱AB中点,则的值为( )
A.﹣1 B.1 C. D.
7.已知变量y关于x的回归方程为y=ebx﹣0.5,其一组数据如表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
8.设(3x+)n的展开式的各项系数之和为M,二项式系数之和为N,若M﹣17N=480,则展开式中含x3项的系数为( )
A.40 B.30 C.20 D.15
9.(x2﹣x+2)(x﹣1)4的展开式中x项的系数为( )
A.﹣9 B.﹣5 C.7 D.8
10.已知(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,(1+λx)n=a0+a1x+a2x2+…+anxn,若a1+a2+…an=242,则a0﹣a1+a2﹣…(﹣1)nan的值为( )
A.1 B.﹣1 C.81 D.﹣81
11.如图,将两个全等等腰直角三角形拼成一个平行四边形ABCD,将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,则直线AC与BD所成角余弦值为( )
A. B. C. D.
12.已知F1,F2是双曲线的左、右焦点,若点F1关于双曲线渐近线的对称点P满足∠OPF2=∠POF2(O为坐标原点),则双曲线的离心率为( )
A. B.2 C. D.
二、填空题
13.把4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,全部分完,不同的分配方案数为 .
14.的展开式中x2的系数为 .
15.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为 .
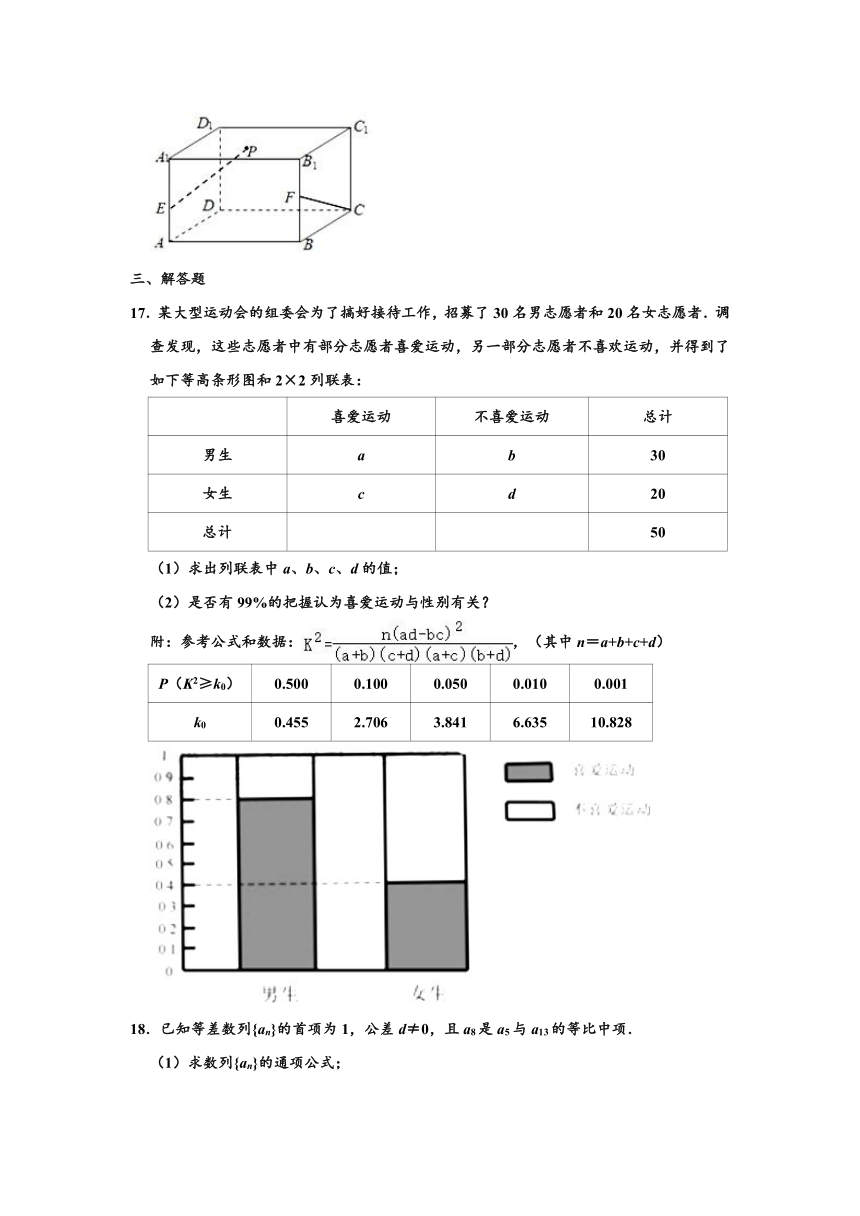
16.如图,在长方体ABCD﹣A1B1C1D1中,AB=1,AA1=2,,E、F分别为棱AA1、BB1的中点.动点P在长方体的表面上,且EP⊥CF,则点P的轨迹的长度为 .
三、解答题
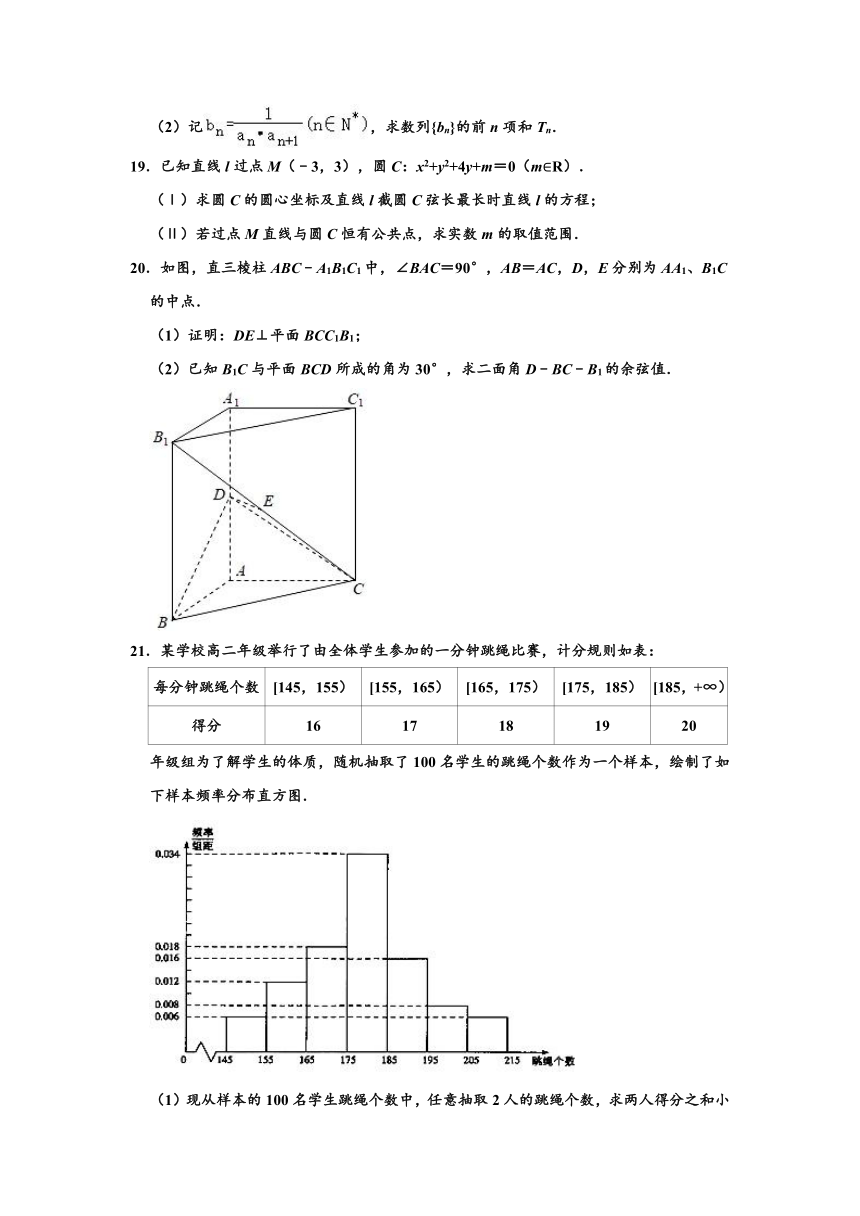
17.某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和2×2列联表:
喜爱运动 不喜爱运动 总计
男生 a b 30
女生 c d 20
总计
50
(1)求出列联表中a、b、c、d的值;
(2)是否有99%的把握认为喜爱运动与性别有关?
附:参考公式和数据:,(其中n=a+b+c+d)
P(K2≥k0) 0.500 0.100 0.050 0.010 0.001
k0 0.455 2.706 3.841 6.635 10.828
18.已知等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)记,求数列{bn}的前n项和Tn.
19.已知直线l过点M(﹣3,3),圆C:x2+y2+4y+m=0(m∈R).
(Ⅰ)求圆C的圆心坐标及直线l截圆C弦长最长时直线l的方程;
(Ⅱ)若过点M直线与圆C恒有公共点,求实数m的取值范围.
20.如图,直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC,D,E分别为AA1、B1C的中点.
(1)证明:DE⊥平面BCC1B1;
(2)已知B1C与平面BCD所成的角为30°,求二面角D﹣BC﹣B1的余弦值.
21.某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如表:
每分钟跳绳个数 [145,155) [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 18 19 20
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数X近似服从正态分布N(μ,σ2),其中σ2≈225,μ为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为ξ,求随机变量ξ的分布列和数学期望与方差.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9554,P(μ﹣3σ<X<μ+3σ)=0.9974.
22.如图,已知椭圆O:+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=﹣2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1?k2为定值;
②求?的取值范围.
参考答案
一、选择题(共12小题).
1.设随机变量ξ服从正态分布N(1,σ2),若P(ξ<2)=0.8,则P(0<ξ<1)的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
【分析】根据随机变量ξ服从正态分布N(1,σ2),看出这组数据对应的正态曲线的对称轴x=1,根据正态曲线的特点,得到P(0<ξ<1)=P(0<ξ<2),得到结果.
解:∵随机变量X服从正态分布N(1,σ2),
∴μ=1,得对称轴是x=1.
∵P(ξ<2)=0.8,
∴P(ξ≥2)=P(ξ<0)=0.2,
∴P(0<ξ<2)=0.6
∴P(0<ξ<1)=0.3.
故选:B.
2.已知=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),若P,A,B,C四点共面,则λ=( )
A.9 B.﹣9 C.﹣3 D.3
【分析】由共面向量定理得,从而(7,6,λ)=x(2,1,﹣3)+y(﹣1,2,3),由此能求出λ的值.
解:∵=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),
P,A,B,C四点共面,
∴,
∴(7,6,λ)=x(2,1,﹣3)+y(﹣1,2,3),
解得λ=﹣9.
故选:B.
3.设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),且⊥,∥,则|+|=( )
A. B. C.3 D.4
【分析】利用向量平行和向量垂直的性质列出方程组,求出x,y,再由平面向量坐标运算法则求出,由此能求出||.
解:设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),
且⊥,∥,
∴,解得x=1,y=﹣2,
∴=(1,1,1)+(1,﹣2,1)=(2,﹣1,2),
∴|+|=.
故选:C.
4.已知空间向量,,且,则向量与(λ≠0)的夹角为( )
A. B.或 C. D.或
【分析】根据 =3求出n的值,再计算cos<,>求出与 的夹角.
解:∵=1+0+n,
解得n=2;
又||=,=(1,1,2),||=,
cos<,>===,
且<,>∈[0,π],
∴与的夹角为;
∴与的夹角为或者.
故选:B.
5.如图,在平行六面体ABCD﹣A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
A. B. C. D.
【分析】用空间向量解答.
解:∵=+﹣;
∴2=(+﹣)2;
即2=?+?﹣?+?+?﹣?﹣(?+?﹣?)
=1+0﹣3×1×cos60°+0+1﹣3×1×cos60°﹣(3×1×cos60°+3×1×cos60°﹣9);
=1﹣+1﹣﹣+9=5,
∴A1C=.
故选:A.
6.在正四面体P﹣ABC中,棱长为2,且E是棱AB中点,则的值为( )
A.﹣1 B.1 C. D.
【分析】运用空间向量基本定理,转化为向量,,为基底.
解:如图,P﹣ABC为正四面体,则∠APC=∠BPC=∠APB=60°,
E是棱AB中点,
所以=,=﹣,
所以=?(﹣)=+﹣﹣=﹣=1﹣2=﹣1,
故选:A.
7.已知变量y关于x的回归方程为y=ebx﹣0.5,其一组数据如表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
【分析】两边同取对数,得到lny=bx﹣0.5,设z=bx﹣0.5,求出b,把x=5代入,求出z,再求出y.
解:两边同取对数,得到lny=bx﹣0.5,
设z=bx﹣0.5,
x 1 2 3 4
z 1 3 4 6
,,
由,得3.5=2.5b﹣0.5,
故b=1.6,
所以z=1.6x﹣0.5,y=e1.6x﹣0.5,
当x=5时,y=e1.6×5﹣0.5=e,
故选:D.
8.设(3x+)n的展开式的各项系数之和为M,二项式系数之和为N,若M﹣17N=480,则展开式中含x3项的系数为( )
A.40 B.30 C.20 D.15
【分析】(3x+)n的展开式的各项系数之和为M,令x=1,可得M=4n.二项式系数之和为N=2n,代入M﹣17N=480,解得n,再利用通项公式即可得出.
解:(3x+)n的展开式的各项系数之和为M,令x=1,可得M=4n.
二项式系数之和为N=2n,
∵M﹣17N=480,∴4n﹣17?2n=480,解得n=5.
∴的通项公式:Tr+1=(3x)5﹣r=35﹣r,
令r=3,解得r=4
展开式中含x3项的系数为×3=15
故选:D.
9.(x2﹣x+2)(x﹣1)4的展开式中x项的系数为( )
A.﹣9 B.﹣5 C.7 D.8
【分析】把(x﹣1)4 按照二项式定理展开,可得(x2﹣x+2)(x﹣1)4的展开式中x项的系数.
解:∵(x2﹣x+2)(x﹣1)4 =(x2﹣x+2)(x4﹣4x3+6x2﹣4x+1),
故它的的展开式中x项的系数为﹣1×1+2×(﹣4)=﹣9,
故选:A.
10.已知(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,(1+λx)n=a0+a1x+a2x2+…+anxn,若a1+a2+…an=242,则a0﹣a1+a2﹣…(﹣1)nan的值为( )
A.1 B.﹣1 C.81 D.﹣81
【分析】先根据已知求得n,再结合对应系数的性质求得λ,即可求得结论.
解:由(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,得:=,解得 n=5,
所以(1+λx)n=(1+λx)5=a0+a1x+a2x2+…+a5x5;
令 x=0,得a0=1,
令x=1得(1+λ)5=a0+a1+a2+…a5=243,
所以1+λ=3,λ=2,
则.
令x=﹣1,得;
故选:B.
11.如图,将两个全等等腰直角三角形拼成一个平行四边形ABCD,将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,则直线AC与BD所成角余弦值为( )
A. B. C. D.
【分析】由平面ABD⊥平面BCD,AB⊥BD,BD⊥CD,得AB⊥平面BDC,以B为原点,BD为x轴,过B作DC的平行线为y轴,BA为z轴,建立空间直角坐标系,利用向量法能求出直线AC与BD所成角余弦值.
解:将两个全等等腰直角三角形拼成一个平行四边形ABCD,
将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,
∵平面ABD⊥平面BCD,AB⊥BD,BD⊥CD,
∴AB⊥平面BDC,
∴以B为原点,BD为x轴,过B作DC的平行线为y轴,BA为z轴,建立空间直角坐标系,
设BD=2,则A(0,0,2),C(2,2,0),B(0,0,0),D(2,0,0),
=(2,2,﹣2),=(2,0,0),
设直线AC与BD所成角为θ,
则直线AC与BD所成角余弦值为:
cosθ===.
故选:C.
12.已知F1,F2是双曲线的左、右焦点,若点F1关于双曲线渐近线的对称点P满足∠OPF2=∠POF2(O为坐标原点),则双曲线的离心率为( )
A. B.2 C. D.
【分析】连接OP,运用等边三角形的定义和垂直平分线的性质,以及点到直线的距离公式,可得|OP|=c,O到PF1的距离为a,再由锐角三角函数的定义可得所求离心率的值.
解:连接OP,可得|OP|=|OF1|=|OF2|=|PF2|=c,
F1到渐近线bx+ay=0的距离为d==b,
在等腰三角形OPF1中,O到PF1的距离为a,
即sin∠OPF1=sin30°==,
可得e==2.
故选:B.
二、填空题
13.把4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,全部分完,不同的分配方案数为 36 .
【分析】由题意知将4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,需要先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,根据分步乘法原理得到结果.
解:∵将4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,
∴先从4个人中选出2个作为一个元素看成整体,
再把它同另外两个元素在三个位置全排列,共有C24A33=36.
故答案为:36.
14.的展开式中x2的系数为 28 .
【分析】先把所给化简,再求出分子的特定项系数即可求解.
解:∵,
∵(x﹣1)8中x6的系数为=28.
∴展开式中x2的系数为.
故答案为:28.
15.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为 .
【分析】由题知,p=1,由抛物线的定义可得,|AF|+|BF|=xA+xB+p,代入数据可得xA+xB=7,再利用中点坐标公式即可得解.
解:由题意可知,p=1,
由抛物线的定义可得,|AF|+|BF|=xA+xB+p=xA+xB+1=8,
∴xA+xB=7,
∴线段AB的中点到y轴的距离为.
故答案为:.
16.如图,在长方体ABCD﹣A1B1C1D1中,AB=1,AA1=2,,E、F分别为棱AA1、BB1的中点.动点P在长方体的表面上,且EP⊥CF,则点P的轨迹的长度为 .
【分析】先过F点作出垂直于CF的平面,那么此平面与长方体所截的交线长度之和即为点P的轨迹,从而求解.
解:如图,过 F 作 CF⊥FM 交 B1C1 于 M,
作B1A1∥MN,交 A1D1于N,连接 EN,
建立如下平面直角坐标系,设,,
那么,解得,
∴CF⊥FM,又EF∥AB,∴CF⊥EF,EF∩FM=F,∴CF⊥平面 EMMN,
故点P的轨迹为四边形EFMN的周长,
其长度为
==.
三、解答题
17.某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和2×2列联表:
喜爱运动 不喜爱运动 总计
男生 a b 30
女生 c d 20
总计
50
(1)求出列联表中a、b、c、d的值;
(2)是否有99%的把握认为喜爱运动与性别有关?
附:参考公式和数据:,(其中n=a+b+c+d)
P(K2≥k0) 0.500 0.100 0.050 0.010 0.001
k0 0.455 2.706 3.841 6.635 10.828
【分析】(1)根据条形图计算a、b、c、d的值;
(2)补充列联表,计算K2,对照临界值得出结论.
解:(1)根据条形图知,男生喜爱运动的人数为a=30×0.8=24(人),
不喜爱运动的人数为b=30×0.2=6(人);
女生喜爱运动的人数是c=20×0.4=8(人),
不喜爱运动的人数为d=20×0.6=12(人);
(2)补充列联表,如下;
喜爱运动 不喜爱运动 总计
男生 24 6 30
女生 8 12 20
总计 32 18 50
计算K2==≈8.333>6.635,
所以有99%的把握认为喜爱运动与性别有关.
18.已知等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)记,求数列{bn}的前n项和Tn.
【分析】(1)由等比数列的中项性质和等差数列的通项公式,解方程可得d,即可得到所求通项公式;
(2)求得bn===(﹣),由裂项相消求和,化简可得所求和.
解:(1)等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项,
可得a82=a5a13,即为(1+7d)2=(1+4d)(1+12d),
解得d=2(0舍去),
可得an=1+2(n﹣1)=2n﹣1;
(2)bn===(﹣),
数列{bn}的前n项和Tn=(1﹣+﹣+…+﹣)
=(1﹣)=.
19.已知直线l过点M(﹣3,3),圆C:x2+y2+4y+m=0(m∈R).
(Ⅰ)求圆C的圆心坐标及直线l截圆C弦长最长时直线l的方程;
(Ⅱ)若过点M直线与圆C恒有公共点,求实数m的取值范围.
【分析】第一步利用直径为最长弦;第二步利用点与圆的位置关系.
解:(Ⅰ)圆C方程标准化为:x2+(y+2)2=4﹣m
∴圆心C的坐标为(0,﹣2)
直线l截圆C弦长最长,即l过圆心,
故此时l的方程为:,
整理得:5x+3y+6=0;
(Ⅱ)若过点M的直线与圆C恒有公共点,
则点M在圆上或圆内,
∴(﹣3)2+32+4×3+m≤0,
得m≤﹣30.
20.如图,直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC,D,E分别为AA1、B1C的中点.
(1)证明:DE⊥平面BCC1B1;
(2)已知B1C与平面BCD所成的角为30°,求二面角D﹣BC﹣B1的余弦值.
【分析】(1)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A﹣xyz.求出与平面BCC1B1中两个不共线的向量的坐标,由数量积为0证明向量垂直,得到DE垂直于平面内两相交直线,可得DE⊥平面BCC1B1;
(2)由B1C与平面BCD所成的角为30°,求出平面BCD的一个法向量,再结合(1)求出平面BCB1的一个法向量,由两法向量所成角的余弦值解得二面角D﹣BC﹣B1的余弦值.
【解答】(1)证明:以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A﹣xyz.
设AB=1,AD=a,则B(1,0,0),C(0,1,0),B1(1,0,2a),D(0,0,a),B1(1,0,2a),
,,,.
∵,,∴DE⊥BC,DE⊥B1C,
又BC∩B1C=C,∴DE⊥平面BCC1B1;
(2)解:设平面BCD的法向量=(x0,y0,z0),
则,又,故,取x0=1,得.
∵B1C与平面BCD所成的角为30°,,
∴|cos<>|=,解得,
∴.
由(1)知平面BCB1的法向量,
∴cos<>==.
∴二面角D﹣BC﹣B1的余弦值为.
21.某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如表:
每分钟跳绳个数 [145,155) [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 18 19 20
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数X近似服从正态分布N(μ,σ2),其中σ2≈225,μ为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为ξ,求随机变量ξ的分布列和数学期望与方差.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9554,P(μ﹣3σ<X<μ+3σ)=0.9974.
【分析】(1)设“两人得分之和小于35分”为事件A,写出事件A包括的四种情况,再由频率分布直方图可得得16分,得17分和得18分的人数,然后利用古典概型概率就送过去求解;
(2)由频率分布直方图可得样本数据的平均数的估计值,再求得标准差σ,可得高二年级全体学生的跳绳个数X近似服从正态分布N(179,152).
(i)利用正态分布的对称性求解;
(ii)由正态分布可得,全年级任取一人,其每分钟跳绳个数在179以上的概率为,则ξ~B(3,),ξ的所有可能的取值为0,1,2,3.分别求出概率,得到ξ的分布列,再由期望公式求期望.
解:(1)设“两人得分之和小于35分”为事件A,则事件A包括以下四种情况:
①两人得分均为16分;②两人中一人16分,一人17分;
③两人中一人16分,一人18分;④两人均17分.
由频率分布直方图可得,得16分的有6人,得17分的有12人,得18分的有18人,
则由古典概型的概率计算公式可得.
∴两人得分之和小于35的概率为;
(2)由频率分布直方图可得样本数据的平均数的估计值为:
0.034×180+0.016×190+0.008×200+0.006×210)×10=179(个).
又由σ2≈225,得标准差σ≈15,
∴高二年级全体学生的跳绳个数X近似服从正态分布N(179,152).
(i)∵μ﹣σ=179﹣15=164,∴,
故高二年级一分钟跳绳个数超过164个的人数估计为2000×0.8413=1682.6≈1683(人);
(ii)由正态分布可得,全年级任取一人,其每分钟跳绳个数在179以上的概率为,
∴ξ~B(3,),ξ的所有可能的取值为0,1,2,3.
∴,,
,,
故ξ的分布列为:
ξ 0 1 2 3
P
∴,.
22.如图,已知椭圆O:+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=﹣2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1?k2为定值;
②求?的取值范围.
【分析】(1)求得椭圆的a,b,c,可得B,C,F的坐标,求得PM的方程代入椭圆方程,可得M,再由BF的方程,求得M到直线BF的距离,再由三角形的面积公式计算即可得到所求值;
(2)①设P(m,﹣2)(m≠0),求得PM的方程,代入椭圆方程求得M的坐标,运用直线的斜率公式计算即可得到k1?k2为定值;
②求得向量PB,PM的坐标,运用向量的数量积的坐标表示,可得?=,令t=4+m2>4,由函数的单调性,可得所求范围.
解:(1)由椭圆的方程+y2=1,可得a=2,b=1,c=,
即有B(0,1),C(0,﹣1),F(,0),
直线PM:+=1,即为y=x﹣1,
代入椭圆方程可得,M(,),
连接BF,可得BF:+y=1,即为x+y﹣=0,
而BF=a=2,M到直线BF的距离为d==,
即有S△MBF=BF?d=?2?=;
(2)①设P(m,﹣2)(m≠0),kPM==﹣,
PM:y=﹣x﹣1,代入椭圆方程可得(4+m2)x2+8mx=0,
解得M(﹣,),k1==m,k2==﹣,
则k1k2=m?(﹣)=﹣为定值;
②由①知,=(﹣m,3),=(﹣﹣m,+2)=(﹣,),
?=﹣m?(﹣)+3?=,
令t=4+m2>4,即有?==t﹣+7,
由y=t﹣+7在(4,+∞)单调递增,则?=t﹣+7>4﹣+7=9,
故?的取值范围为(9,+∞).
一、选择题(共12小题).
1.设随机变量ξ服从正态分布N(1,σ2),若P(ξ<2)=0.8,则P(0<ξ<1)的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
2.已知=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),若P,A,B,C四点共面,则λ=( )
A.9 B.﹣9 C.﹣3 D.3
3.设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),且⊥,∥,则|+|=( )
A. B. C.3 D.4
4.已知空间向量,,且,则向量与(λ≠0)的夹角为( )
A. B.或 C. D.或
5.如图,在平行六面体ABCD﹣A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
A. B. C. D.
6.在正四面体P﹣ABC中,棱长为2,且E是棱AB中点,则的值为( )
A.﹣1 B.1 C. D.
7.已知变量y关于x的回归方程为y=ebx﹣0.5,其一组数据如表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
8.设(3x+)n的展开式的各项系数之和为M,二项式系数之和为N,若M﹣17N=480,则展开式中含x3项的系数为( )
A.40 B.30 C.20 D.15
9.(x2﹣x+2)(x﹣1)4的展开式中x项的系数为( )
A.﹣9 B.﹣5 C.7 D.8
10.已知(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,(1+λx)n=a0+a1x+a2x2+…+anxn,若a1+a2+…an=242,则a0﹣a1+a2﹣…(﹣1)nan的值为( )
A.1 B.﹣1 C.81 D.﹣81
11.如图,将两个全等等腰直角三角形拼成一个平行四边形ABCD,将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,则直线AC与BD所成角余弦值为( )
A. B. C. D.
12.已知F1,F2是双曲线的左、右焦点,若点F1关于双曲线渐近线的对称点P满足∠OPF2=∠POF2(O为坐标原点),则双曲线的离心率为( )
A. B.2 C. D.
二、填空题
13.把4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,全部分完,不同的分配方案数为 .
14.的展开式中x2的系数为 .
15.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为 .
16.如图,在长方体ABCD﹣A1B1C1D1中,AB=1,AA1=2,,E、F分别为棱AA1、BB1的中点.动点P在长方体的表面上,且EP⊥CF,则点P的轨迹的长度为 .
三、解答题
17.某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和2×2列联表:
喜爱运动 不喜爱运动 总计
男生 a b 30
女生 c d 20
总计
50
(1)求出列联表中a、b、c、d的值;
(2)是否有99%的把握认为喜爱运动与性别有关?
附:参考公式和数据:,(其中n=a+b+c+d)
P(K2≥k0) 0.500 0.100 0.050 0.010 0.001
k0 0.455 2.706 3.841 6.635 10.828
18.已知等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)记,求数列{bn}的前n项和Tn.
19.已知直线l过点M(﹣3,3),圆C:x2+y2+4y+m=0(m∈R).
(Ⅰ)求圆C的圆心坐标及直线l截圆C弦长最长时直线l的方程;
(Ⅱ)若过点M直线与圆C恒有公共点,求实数m的取值范围.
20.如图,直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC,D,E分别为AA1、B1C的中点.
(1)证明:DE⊥平面BCC1B1;
(2)已知B1C与平面BCD所成的角为30°,求二面角D﹣BC﹣B1的余弦值.
21.某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如表:
每分钟跳绳个数 [145,155) [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 18 19 20
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数X近似服从正态分布N(μ,σ2),其中σ2≈225,μ为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为ξ,求随机变量ξ的分布列和数学期望与方差.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9554,P(μ﹣3σ<X<μ+3σ)=0.9974.
22.如图,已知椭圆O:+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=﹣2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1?k2为定值;
②求?的取值范围.
参考答案
一、选择题(共12小题).
1.设随机变量ξ服从正态分布N(1,σ2),若P(ξ<2)=0.8,则P(0<ξ<1)的值为( )
A.0.2 B.0.3 C.0.4 D.0.6
【分析】根据随机变量ξ服从正态分布N(1,σ2),看出这组数据对应的正态曲线的对称轴x=1,根据正态曲线的特点,得到P(0<ξ<1)=P(0<ξ<2),得到结果.
解:∵随机变量X服从正态分布N(1,σ2),
∴μ=1,得对称轴是x=1.
∵P(ξ<2)=0.8,
∴P(ξ≥2)=P(ξ<0)=0.2,
∴P(0<ξ<2)=0.6
∴P(0<ξ<1)=0.3.
故选:B.
2.已知=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),若P,A,B,C四点共面,则λ=( )
A.9 B.﹣9 C.﹣3 D.3
【分析】由共面向量定理得,从而(7,6,λ)=x(2,1,﹣3)+y(﹣1,2,3),由此能求出λ的值.
解:∵=(2,1,﹣3),=(﹣1,2,3),=(7,6,λ),
P,A,B,C四点共面,
∴,
∴(7,6,λ)=x(2,1,﹣3)+y(﹣1,2,3),
解得λ=﹣9.
故选:B.
3.设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),且⊥,∥,则|+|=( )
A. B. C.3 D.4
【分析】利用向量平行和向量垂直的性质列出方程组,求出x,y,再由平面向量坐标运算法则求出,由此能求出||.
解:设x,y∈R,向量=(x,1,1),=(1,y,1),=(2,﹣4,2),
且⊥,∥,
∴,解得x=1,y=﹣2,
∴=(1,1,1)+(1,﹣2,1)=(2,﹣1,2),
∴|+|=.
故选:C.
4.已知空间向量,,且,则向量与(λ≠0)的夹角为( )
A. B.或 C. D.或
【分析】根据 =3求出n的值,再计算cos<,>求出与 的夹角.
解:∵=1+0+n,
解得n=2;
又||=,=(1,1,2),||=,
cos<,>===,
且<,>∈[0,π],
∴与的夹角为;
∴与的夹角为或者.
故选:B.
5.如图,在平行六面体ABCD﹣A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60°,且A1A=3,则A1C的长为( )
A. B. C. D.
【分析】用空间向量解答.
解:∵=+﹣;
∴2=(+﹣)2;
即2=?+?﹣?+?+?﹣?﹣(?+?﹣?)
=1+0﹣3×1×cos60°+0+1﹣3×1×cos60°﹣(3×1×cos60°+3×1×cos60°﹣9);
=1﹣+1﹣﹣+9=5,
∴A1C=.
故选:A.
6.在正四面体P﹣ABC中,棱长为2,且E是棱AB中点,则的值为( )
A.﹣1 B.1 C. D.
【分析】运用空间向量基本定理,转化为向量,,为基底.
解:如图,P﹣ABC为正四面体,则∠APC=∠BPC=∠APB=60°,
E是棱AB中点,
所以=,=﹣,
所以=?(﹣)=+﹣﹣=﹣=1﹣2=﹣1,
故选:A.
7.已知变量y关于x的回归方程为y=ebx﹣0.5,其一组数据如表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
【分析】两边同取对数,得到lny=bx﹣0.5,设z=bx﹣0.5,求出b,把x=5代入,求出z,再求出y.
解:两边同取对数,得到lny=bx﹣0.5,
设z=bx﹣0.5,
x 1 2 3 4
z 1 3 4 6
,,
由,得3.5=2.5b﹣0.5,
故b=1.6,
所以z=1.6x﹣0.5,y=e1.6x﹣0.5,
当x=5时,y=e1.6×5﹣0.5=e,
故选:D.
8.设(3x+)n的展开式的各项系数之和为M,二项式系数之和为N,若M﹣17N=480,则展开式中含x3项的系数为( )
A.40 B.30 C.20 D.15
【分析】(3x+)n的展开式的各项系数之和为M,令x=1,可得M=4n.二项式系数之和为N=2n,代入M﹣17N=480,解得n,再利用通项公式即可得出.
解:(3x+)n的展开式的各项系数之和为M,令x=1,可得M=4n.
二项式系数之和为N=2n,
∵M﹣17N=480,∴4n﹣17?2n=480,解得n=5.
∴的通项公式:Tr+1=(3x)5﹣r=35﹣r,
令r=3,解得r=4
展开式中含x3项的系数为×3=15
故选:D.
9.(x2﹣x+2)(x﹣1)4的展开式中x项的系数为( )
A.﹣9 B.﹣5 C.7 D.8
【分析】把(x﹣1)4 按照二项式定理展开,可得(x2﹣x+2)(x﹣1)4的展开式中x项的系数.
解:∵(x2﹣x+2)(x﹣1)4 =(x2﹣x+2)(x4﹣4x3+6x2﹣4x+1),
故它的的展开式中x项的系数为﹣1×1+2×(﹣4)=﹣9,
故选:A.
10.已知(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,(1+λx)n=a0+a1x+a2x2+…+anxn,若a1+a2+…an=242,则a0﹣a1+a2﹣…(﹣1)nan的值为( )
A.1 B.﹣1 C.81 D.﹣81
【分析】先根据已知求得n,再结合对应系数的性质求得λ,即可求得结论.
解:由(1+λx)n展开式中第三项的二项式系数与第四项的二项式系数相等,得:=,解得 n=5,
所以(1+λx)n=(1+λx)5=a0+a1x+a2x2+…+a5x5;
令 x=0,得a0=1,
令x=1得(1+λ)5=a0+a1+a2+…a5=243,
所以1+λ=3,λ=2,
则.
令x=﹣1,得;
故选:B.
11.如图,将两个全等等腰直角三角形拼成一个平行四边形ABCD,将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,则直线AC与BD所成角余弦值为( )
A. B. C. D.
【分析】由平面ABD⊥平面BCD,AB⊥BD,BD⊥CD,得AB⊥平面BDC,以B为原点,BD为x轴,过B作DC的平行线为y轴,BA为z轴,建立空间直角坐标系,利用向量法能求出直线AC与BD所成角余弦值.
解:将两个全等等腰直角三角形拼成一个平行四边形ABCD,
将平行四边形ABCD沿对角线BD折起,使平面ABD⊥平面BCD,
∵平面ABD⊥平面BCD,AB⊥BD,BD⊥CD,
∴AB⊥平面BDC,
∴以B为原点,BD为x轴,过B作DC的平行线为y轴,BA为z轴,建立空间直角坐标系,
设BD=2,则A(0,0,2),C(2,2,0),B(0,0,0),D(2,0,0),
=(2,2,﹣2),=(2,0,0),
设直线AC与BD所成角为θ,
则直线AC与BD所成角余弦值为:
cosθ===.
故选:C.
12.已知F1,F2是双曲线的左、右焦点,若点F1关于双曲线渐近线的对称点P满足∠OPF2=∠POF2(O为坐标原点),则双曲线的离心率为( )
A. B.2 C. D.
【分析】连接OP,运用等边三角形的定义和垂直平分线的性质,以及点到直线的距离公式,可得|OP|=c,O到PF1的距离为a,再由锐角三角函数的定义可得所求离心率的值.
解:连接OP,可得|OP|=|OF1|=|OF2|=|PF2|=c,
F1到渐近线bx+ay=0的距离为d==b,
在等腰三角形OPF1中,O到PF1的距离为a,
即sin∠OPF1=sin30°==,
可得e==2.
故选:B.
二、填空题
13.把4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,全部分完,不同的分配方案数为 36 .
【分析】由题意知将4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,需要先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,根据分步乘法原理得到结果.
解:∵将4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,
∴先从4个人中选出2个作为一个元素看成整体,
再把它同另外两个元素在三个位置全排列,共有C24A33=36.
故答案为:36.
14.的展开式中x2的系数为 28 .
【分析】先把所给化简,再求出分子的特定项系数即可求解.
解:∵,
∵(x﹣1)8中x6的系数为=28.
∴展开式中x2的系数为.
故答案为:28.
15.已知F是抛物线y2=2x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=8,则线段AB的中点到y轴的距离为 .
【分析】由题知,p=1,由抛物线的定义可得,|AF|+|BF|=xA+xB+p,代入数据可得xA+xB=7,再利用中点坐标公式即可得解.
解:由题意可知,p=1,
由抛物线的定义可得,|AF|+|BF|=xA+xB+p=xA+xB+1=8,
∴xA+xB=7,
∴线段AB的中点到y轴的距离为.
故答案为:.
16.如图,在长方体ABCD﹣A1B1C1D1中,AB=1,AA1=2,,E、F分别为棱AA1、BB1的中点.动点P在长方体的表面上,且EP⊥CF,则点P的轨迹的长度为 .
【分析】先过F点作出垂直于CF的平面,那么此平面与长方体所截的交线长度之和即为点P的轨迹,从而求解.
解:如图,过 F 作 CF⊥FM 交 B1C1 于 M,
作B1A1∥MN,交 A1D1于N,连接 EN,
建立如下平面直角坐标系,设,,
那么,解得,
∴CF⊥FM,又EF∥AB,∴CF⊥EF,EF∩FM=F,∴CF⊥平面 EMMN,
故点P的轨迹为四边形EFMN的周长,
其长度为
==.
三、解答题
17.某大型运动会的组委会为了搞好接待工作,招募了30名男志愿者和20名女志愿者.调查发现,这些志愿者中有部分志愿者喜爱运动,另一部分志愿者不喜欢运动,并得到了如下等高条形图和2×2列联表:
喜爱运动 不喜爱运动 总计
男生 a b 30
女生 c d 20
总计
50
(1)求出列联表中a、b、c、d的值;
(2)是否有99%的把握认为喜爱运动与性别有关?
附:参考公式和数据:,(其中n=a+b+c+d)
P(K2≥k0) 0.500 0.100 0.050 0.010 0.001
k0 0.455 2.706 3.841 6.635 10.828
【分析】(1)根据条形图计算a、b、c、d的值;
(2)补充列联表,计算K2,对照临界值得出结论.
解:(1)根据条形图知,男生喜爱运动的人数为a=30×0.8=24(人),
不喜爱运动的人数为b=30×0.2=6(人);
女生喜爱运动的人数是c=20×0.4=8(人),
不喜爱运动的人数为d=20×0.6=12(人);
(2)补充列联表,如下;
喜爱运动 不喜爱运动 总计
男生 24 6 30
女生 8 12 20
总计 32 18 50
计算K2==≈8.333>6.635,
所以有99%的把握认为喜爱运动与性别有关.
18.已知等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项.
(1)求数列{an}的通项公式;
(2)记,求数列{bn}的前n项和Tn.
【分析】(1)由等比数列的中项性质和等差数列的通项公式,解方程可得d,即可得到所求通项公式;
(2)求得bn===(﹣),由裂项相消求和,化简可得所求和.
解:(1)等差数列{an}的首项为1,公差d≠0,且a8是a5与a13的等比中项,
可得a82=a5a13,即为(1+7d)2=(1+4d)(1+12d),
解得d=2(0舍去),
可得an=1+2(n﹣1)=2n﹣1;
(2)bn===(﹣),
数列{bn}的前n项和Tn=(1﹣+﹣+…+﹣)
=(1﹣)=.
19.已知直线l过点M(﹣3,3),圆C:x2+y2+4y+m=0(m∈R).
(Ⅰ)求圆C的圆心坐标及直线l截圆C弦长最长时直线l的方程;
(Ⅱ)若过点M直线与圆C恒有公共点,求实数m的取值范围.
【分析】第一步利用直径为最长弦;第二步利用点与圆的位置关系.
解:(Ⅰ)圆C方程标准化为:x2+(y+2)2=4﹣m
∴圆心C的坐标为(0,﹣2)
直线l截圆C弦长最长,即l过圆心,
故此时l的方程为:,
整理得:5x+3y+6=0;
(Ⅱ)若过点M的直线与圆C恒有公共点,
则点M在圆上或圆内,
∴(﹣3)2+32+4×3+m≤0,
得m≤﹣30.
20.如图,直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC,D,E分别为AA1、B1C的中点.
(1)证明:DE⊥平面BCC1B1;
(2)已知B1C与平面BCD所成的角为30°,求二面角D﹣BC﹣B1的余弦值.
【分析】(1)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A﹣xyz.求出与平面BCC1B1中两个不共线的向量的坐标,由数量积为0证明向量垂直,得到DE垂直于平面内两相交直线,可得DE⊥平面BCC1B1;
(2)由B1C与平面BCD所成的角为30°,求出平面BCD的一个法向量,再结合(1)求出平面BCB1的一个法向量,由两法向量所成角的余弦值解得二面角D﹣BC﹣B1的余弦值.
【解答】(1)证明:以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A﹣xyz.
设AB=1,AD=a,则B(1,0,0),C(0,1,0),B1(1,0,2a),D(0,0,a),B1(1,0,2a),
,,,.
∵,,∴DE⊥BC,DE⊥B1C,
又BC∩B1C=C,∴DE⊥平面BCC1B1;
(2)解:设平面BCD的法向量=(x0,y0,z0),
则,又,故,取x0=1,得.
∵B1C与平面BCD所成的角为30°,,
∴|cos<>|=,解得,
∴.
由(1)知平面BCB1的法向量,
∴cos<>==.
∴二面角D﹣BC﹣B1的余弦值为.
21.某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如表:
每分钟跳绳个数 [145,155) [155,165) [165,175) [175,185) [185,+∞)
得分 16 17 18 19 20
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数X近似服从正态分布N(μ,σ2),其中σ2≈225,μ为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为ξ,求随机变量ξ的分布列和数学期望与方差.
附:若随机变量X服从正态分布N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9554,P(μ﹣3σ<X<μ+3σ)=0.9974.
【分析】(1)设“两人得分之和小于35分”为事件A,写出事件A包括的四种情况,再由频率分布直方图可得得16分,得17分和得18分的人数,然后利用古典概型概率就送过去求解;
(2)由频率分布直方图可得样本数据的平均数的估计值,再求得标准差σ,可得高二年级全体学生的跳绳个数X近似服从正态分布N(179,152).
(i)利用正态分布的对称性求解;
(ii)由正态分布可得,全年级任取一人,其每分钟跳绳个数在179以上的概率为,则ξ~B(3,),ξ的所有可能的取值为0,1,2,3.分别求出概率,得到ξ的分布列,再由期望公式求期望.
解:(1)设“两人得分之和小于35分”为事件A,则事件A包括以下四种情况:
①两人得分均为16分;②两人中一人16分,一人17分;
③两人中一人16分,一人18分;④两人均17分.
由频率分布直方图可得,得16分的有6人,得17分的有12人,得18分的有18人,
则由古典概型的概率计算公式可得.
∴两人得分之和小于35的概率为;
(2)由频率分布直方图可得样本数据的平均数的估计值为:
0.034×180+0.016×190+0.008×200+0.006×210)×10=179(个).
又由σ2≈225,得标准差σ≈15,
∴高二年级全体学生的跳绳个数X近似服从正态分布N(179,152).
(i)∵μ﹣σ=179﹣15=164,∴,
故高二年级一分钟跳绳个数超过164个的人数估计为2000×0.8413=1682.6≈1683(人);
(ii)由正态分布可得,全年级任取一人,其每分钟跳绳个数在179以上的概率为,
∴ξ~B(3,),ξ的所有可能的取值为0,1,2,3.
∴,,
,,
故ξ的分布列为:
ξ 0 1 2 3
P
∴,.
22.如图,已知椭圆O:+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=﹣2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
(1)当直线PM过椭圆的右焦点F时,求△FBM的面积;
(2)①记直线BM,BP的斜率分别为k1,k2,求证:k1?k2为定值;
②求?的取值范围.
【分析】(1)求得椭圆的a,b,c,可得B,C,F的坐标,求得PM的方程代入椭圆方程,可得M,再由BF的方程,求得M到直线BF的距离,再由三角形的面积公式计算即可得到所求值;
(2)①设P(m,﹣2)(m≠0),求得PM的方程,代入椭圆方程求得M的坐标,运用直线的斜率公式计算即可得到k1?k2为定值;
②求得向量PB,PM的坐标,运用向量的数量积的坐标表示,可得?=,令t=4+m2>4,由函数的单调性,可得所求范围.
解:(1)由椭圆的方程+y2=1,可得a=2,b=1,c=,
即有B(0,1),C(0,﹣1),F(,0),
直线PM:+=1,即为y=x﹣1,
代入椭圆方程可得,M(,),
连接BF,可得BF:+y=1,即为x+y﹣=0,
而BF=a=2,M到直线BF的距离为d==,
即有S△MBF=BF?d=?2?=;
(2)①设P(m,﹣2)(m≠0),kPM==﹣,
PM:y=﹣x﹣1,代入椭圆方程可得(4+m2)x2+8mx=0,
解得M(﹣,),k1==m,k2==﹣,
则k1k2=m?(﹣)=﹣为定值;
②由①知,=(﹣m,3),=(﹣﹣m,+2)=(﹣,),
?=﹣m?(﹣)+3?=,
令t=4+m2>4,即有?==t﹣+7,
由y=t﹣+7在(4,+∞)单调递增,则?=t﹣+7>4﹣+7=9,
故?的取值范围为(9,+∞).
同课章节目录
