向量的减法及其几何意义
图片预览





文档简介
(共22张PPT)
2.2.2向量的减法运算及其几何意义
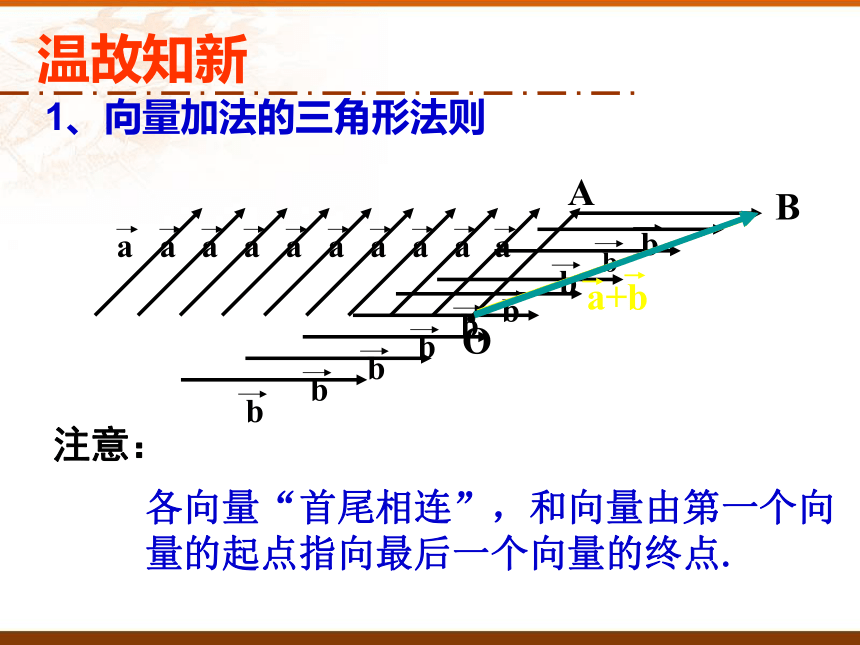
1、向量加法的三角形法则
b
a
O
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
B
b
a
A
注意:
a+b
各向量“首尾相连”,和向量由第一个向量的起点指向最后一个向量的终点.
温故知新
b
a
A
a
a
a
a
a
a
a
a
b
b
b
B
b
a
D
a
C
b
a+b
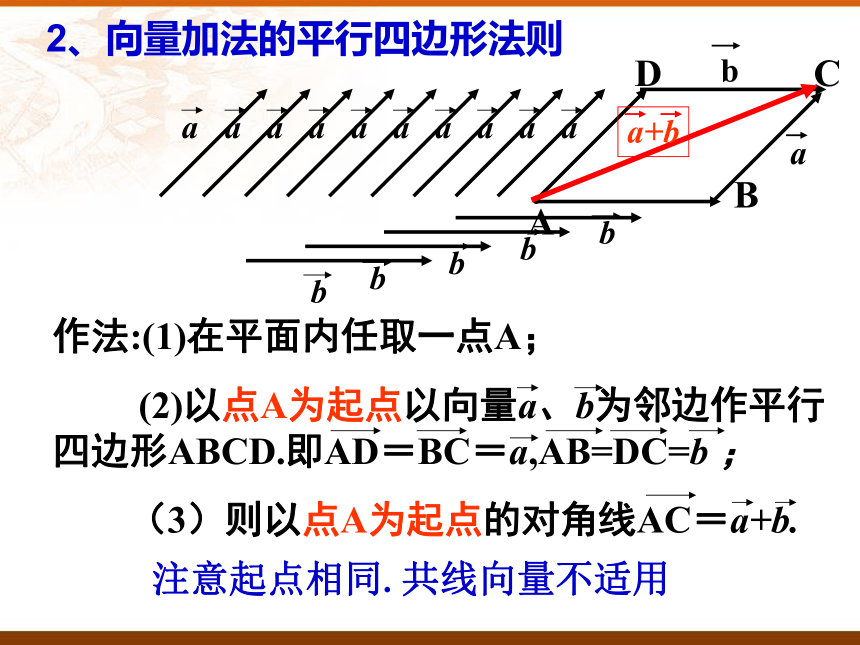
作法:(1)在平面内任取一点A;
(2)以点A为起点以向量a、b为邻边作平行 四边形ABCD.即AD=BC=a,AB=DC=b ;
(3)则以点A为起点的对角线AC=a+b.
2、向量加法的平行四边形法则
注意起点相同.共线向量不适用
练习2:判断下列命题是否正确。
①如果模不相等的非零向量 与 的方向相同或相反,那么
的方向必与 其中之一的方向相同;
②△ABC中,必有 ;
③若 ,则A、B、C为一个三角形的三个顶点;
④若 均为非零向量,则 与 一定相等.
复习:
向量的减法
自主探究
看书 P94~96(限时5分钟)
学习目标:
通过实例,掌握向量的减法运算及理解其几何意义。熟练运用减法的“三角形法则”并与加法法则作比较.
先学后教
与向量 长度相等,方向相反的向量叫做向量 的相反向量,记做 。
介绍一个新的概念——相反向量
A
B
a
-a
C
D
阅读反馈
练习
说明:1、 与 互为相反向量
2、零向量的相反向量仍是零向量
3、任一向量和它相反向量的和是零向量
由此,我们得到:
减去一个向量等于加上这个向量的相反向量
一、减法运算的定义
C
D
二、向量减法的三角形法则
O
A
B
a
b
.
注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
2、差向量的终点指向被减向量的终点
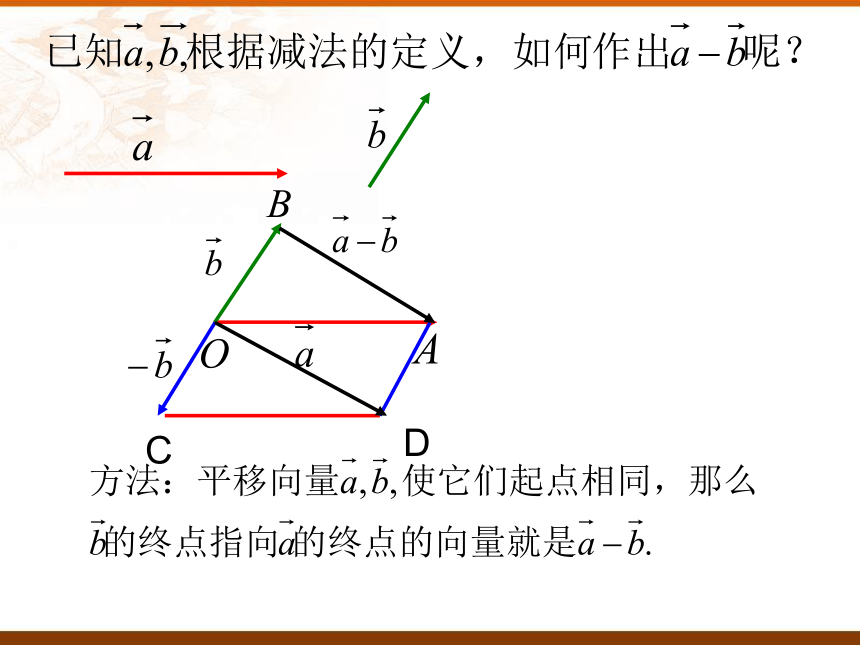
向量减法的几何意义:
可以表示为从向量 的
终点指向向量 的终点的向量.
练习
1.共线同向
2.共线反向
B
A
C
A
B
C
限时训练(3分钟)
P87 练习1、2、3
体验
数学
练习
(1)
(2)
(3)
(4)
练习
(1)
(2)
(3)
(4)
例2:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。
A
D
B
C
a
b
练习2
Come on!
(一)知识
1.理解相反向量的概念
2. 理解向量减法的定义及其几何意义
3. 正确熟练地掌握向量减法的三角形法则:
1)共起点
2)连终点
3)方向指向被减向量的终点
小结:
(二)方法
类比,数形结合,几何作图,分类讨论等思想方法
作业:
P91 6. 8
数学使人聪颖
数学使人严谨
数学使人深刻
数学使人缜密
数学使人坚毅
数学使人智慧
2.2.2向量的减法运算及其几何意义
1、向量加法的三角形法则
b
a
O
a
a
a
a
a
a
a
a
b
b
b
b
b
b
b
B
b
a
A
注意:
a+b
各向量“首尾相连”,和向量由第一个向量的起点指向最后一个向量的终点.
温故知新
b
a
A
a
a
a
a
a
a
a
a
b
b
b
B
b
a
D
a
C
b
a+b
作法:(1)在平面内任取一点A;
(2)以点A为起点以向量a、b为邻边作平行 四边形ABCD.即AD=BC=a,AB=DC=b ;
(3)则以点A为起点的对角线AC=a+b.
2、向量加法的平行四边形法则
注意起点相同.共线向量不适用
练习2:判断下列命题是否正确。
①如果模不相等的非零向量 与 的方向相同或相反,那么
的方向必与 其中之一的方向相同;
②△ABC中,必有 ;
③若 ,则A、B、C为一个三角形的三个顶点;
④若 均为非零向量,则 与 一定相等.
复习:
向量的减法
自主探究
看书 P94~96(限时5分钟)
学习目标:
通过实例,掌握向量的减法运算及理解其几何意义。熟练运用减法的“三角形法则”并与加法法则作比较.
先学后教
与向量 长度相等,方向相反的向量叫做向量 的相反向量,记做 。
介绍一个新的概念——相反向量
A
B
a
-a
C
D
阅读反馈
练习
说明:1、 与 互为相反向量
2、零向量的相反向量仍是零向量
3、任一向量和它相反向量的和是零向量
由此,我们得到:
减去一个向量等于加上这个向量的相反向量
一、减法运算的定义
C
D
二、向量减法的三角形法则
O
A
B
a
b
.
注意:
1、两个向量相减,则表示两个向量起点的字母必须相同
2、差向量的终点指向被减向量的终点
向量减法的几何意义:
可以表示为从向量 的
终点指向向量 的终点的向量.
练习
1.共线同向
2.共线反向
B
A
C
A
B
C
限时训练(3分钟)
P87 练习1、2、3
体验
数学
练习
(1)
(2)
(3)
(4)
练习
(1)
(2)
(3)
(4)
例2:如图,平行四边形ABCD,AB=a,AD=b,用a、b表示向量AC、DB。
A
D
B
C
a
b
练习2
Come on!
(一)知识
1.理解相反向量的概念
2. 理解向量减法的定义及其几何意义
3. 正确熟练地掌握向量减法的三角形法则:
1)共起点
2)连终点
3)方向指向被减向量的终点
小结:
(二)方法
类比,数形结合,几何作图,分类讨论等思想方法
作业:
P91 6. 8
数学使人聪颖
数学使人严谨
数学使人深刻
数学使人缜密
数学使人坚毅
数学使人智慧
