数学:2.2.3《向量数乘及几何意义》课件(新人教a版必修4)
文档属性
| 名称 | 数学:2.2.3《向量数乘及几何意义》课件(新人教a版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 117.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-06 21:02:23 | ||
图片预览



文档简介
(共17张PPT)
2.2.3 向量数乘运算及其几何意义
问题提出
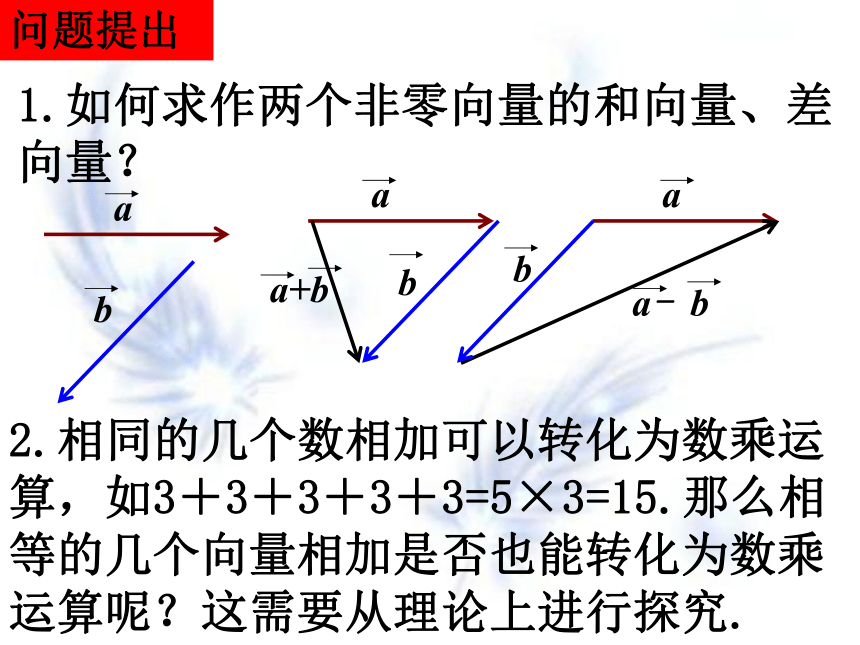
1.如何求作两个非零向量的和向量、差向量?
2.相同的几个数相加可以转化为数乘运算,如3+3+3+3+3=5×3=15.那么相等的几个向量相加是否也能转化为数乘运算呢?这需要从理论上进行探究.
a
b
b
a
a+b
a
a- b
b
探究一:向量的数乘运算及其几何意义
a+a+a记为3a,
(-a)+(-a)+(-a)记为-3a.
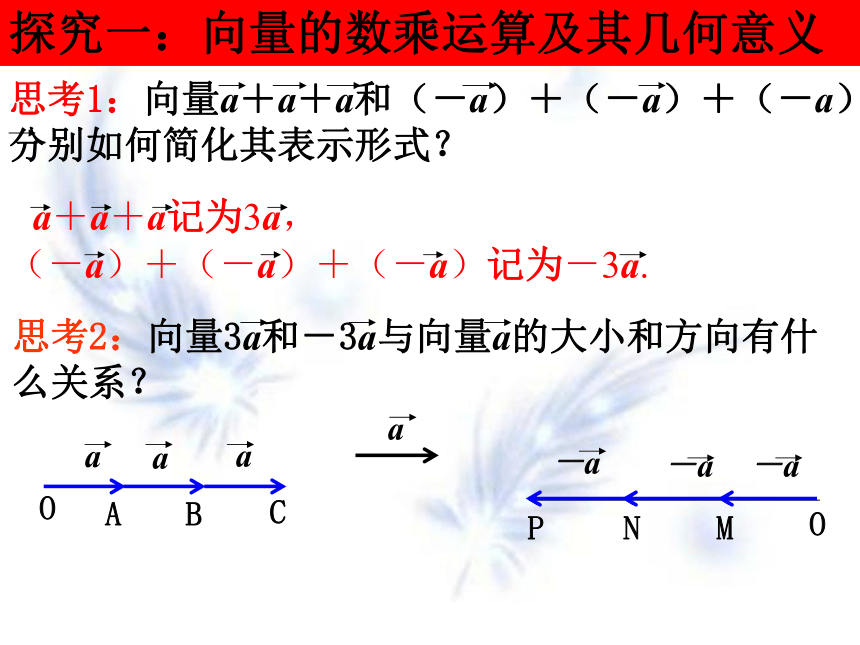
思考1:向量a+a+a和(-a)+(-a)+(-a)分别如何简化其表示形式?
思考2:向量3a和-3a与向量a的大小和方向有什么关系?
a
O
a
a
A
B
C
a
-a
-a
-a
O
M
N
P
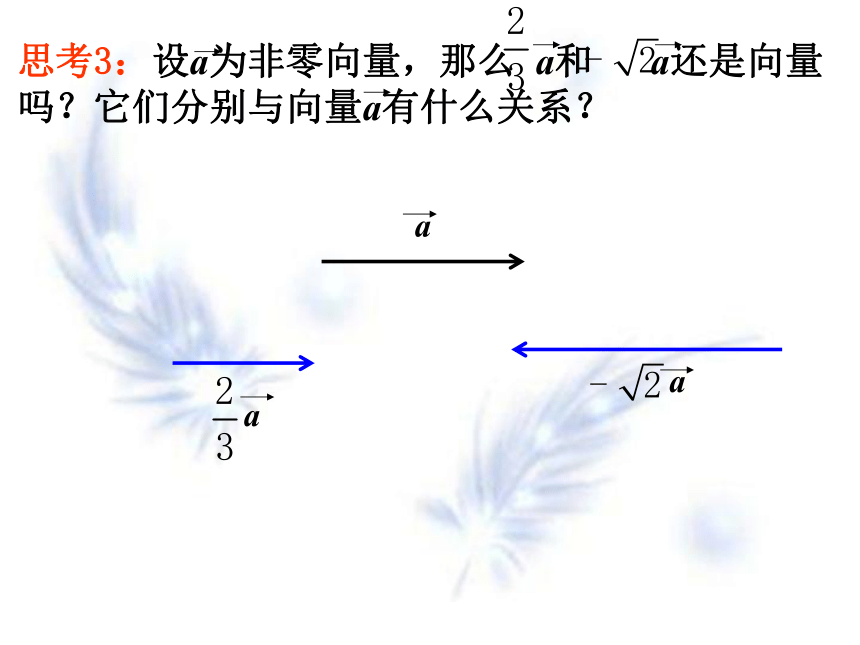
思考3:设a为非零向量,那么 a和 a还是向量吗?它们分别与向量a有什么关系?
a
a
a
思考4: 一般地,我们规定:实数λ与向量a的积是一个向量,这种运算叫做向量的数乘.记作 ,该向量的长度与方向与向量a有什么关系?
(1)|λa|=|λ||a|;
(2)λ>0时,λa与a方向相同;
λ<0时,λa与a方向相反;
λ=0时,λa =0.
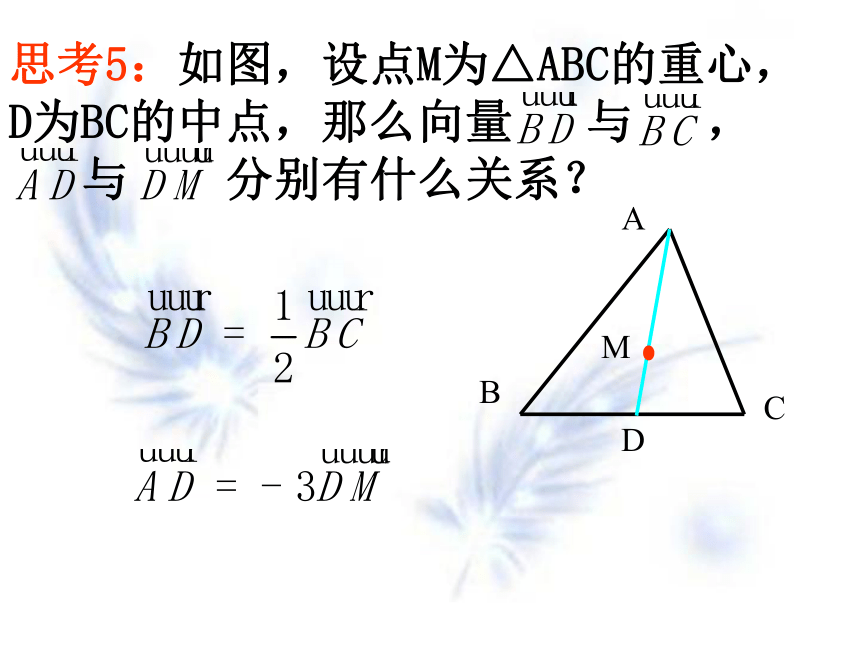
思考5:如图,设点M为△ABC的重心,D为BC的中点,那么向量 与 ,
与 分别有什么关系?
A
B
C
D
M
探究二:向量的数乘运算性质
思考1:你认为-2×(5a),2a+2b, a可分别转化为什么运算?
-2× (5a)= -10a ;
2a + 2b = 2(a+b);
(3+ )a =3a+ a.
思考2:一般地,设λ,μ为实数,λ(μa),(λ+μ) a,λ(a+b)分别等于什么?
λ(μa)=(λμ) a ;
(λ+μ) a =λa +μa;
λ(a+ b)=λa+λb.
例1.计算:
(1)
(2)
(3)
注:向量与实数之间可以象多项式一 样进行运算.
限时练习 (限时4分钟)
P90 练习 3、5
思考3:对于向量a(a≠0)和b,若存在实数λ,使b=λa,则向量a与b的方向有什么关系?
思考4:若向量a(a≠0)与b共线,则一定存在实数λ,使b=λa成立吗?
思考5:综上可得向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa. 若a=0,上述定理成立吗?
思考6:若存在实数λ,使 ,则A、B、C三点的位置关系如何?
思考7:如图,若P为AB的中点,则
与 、 的关系如何?
A
B
P
O
λ(xa±yb)=λxa±λyb.
思考8:向量的加、减、数乘运算统称为向量的线性运算,对于任意向量a、b,以及任意实数λ、x、y,λ(xa±yb)可转化为什么运算?
A
B
C
a
b
3b
2b
a
b
O
例2 如图,已知任意两个非零向量a, b,试作 =a+b, =a+2b,
=a+3b.你能判断A、B、C三点之间的位置关系吗?为什么?
思考:
例3 如图,平行四边形ABCD的两条对角线相交于点M,且 =a, =b,试用a,b表示向量 、 、 、
M
A B
D C
a
b
小结作业
1.实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
2.若λa=0,则可能有λ=0,也可能有a=0.
3.向量的数乘运算律,不是规定,而是可以证明的结论.向量共线定理是平面几何中证明三点共线,直线平行,线段数量关系的理论依据.
作业:
P90练习:3,4,5,6.
2.2.3 向量数乘运算及其几何意义
问题提出
1.如何求作两个非零向量的和向量、差向量?
2.相同的几个数相加可以转化为数乘运算,如3+3+3+3+3=5×3=15.那么相等的几个向量相加是否也能转化为数乘运算呢?这需要从理论上进行探究.
a
b
b
a
a+b
a
a- b
b
探究一:向量的数乘运算及其几何意义
a+a+a记为3a,
(-a)+(-a)+(-a)记为-3a.
思考1:向量a+a+a和(-a)+(-a)+(-a)分别如何简化其表示形式?
思考2:向量3a和-3a与向量a的大小和方向有什么关系?
a
O
a
a
A
B
C
a
-a
-a
-a
O
M
N
P
思考3:设a为非零向量,那么 a和 a还是向量吗?它们分别与向量a有什么关系?
a
a
a
思考4: 一般地,我们规定:实数λ与向量a的积是一个向量,这种运算叫做向量的数乘.记作 ,该向量的长度与方向与向量a有什么关系?
(1)|λa|=|λ||a|;
(2)λ>0时,λa与a方向相同;
λ<0时,λa与a方向相反;
λ=0时,λa =0.
思考5:如图,设点M为△ABC的重心,D为BC的中点,那么向量 与 ,
与 分别有什么关系?
A
B
C
D
M
探究二:向量的数乘运算性质
思考1:你认为-2×(5a),2a+2b, a可分别转化为什么运算?
-2× (5a)= -10a ;
2a + 2b = 2(a+b);
(3+ )a =3a+ a.
思考2:一般地,设λ,μ为实数,λ(μa),(λ+μ) a,λ(a+b)分别等于什么?
λ(μa)=(λμ) a ;
(λ+μ) a =λa +μa;
λ(a+ b)=λa+λb.
例1.计算:
(1)
(2)
(3)
注:向量与实数之间可以象多项式一 样进行运算.
限时练习 (限时4分钟)
P90 练习 3、5
思考3:对于向量a(a≠0)和b,若存在实数λ,使b=λa,则向量a与b的方向有什么关系?
思考4:若向量a(a≠0)与b共线,则一定存在实数λ,使b=λa成立吗?
思考5:综上可得向量共线定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使b=λa. 若a=0,上述定理成立吗?
思考6:若存在实数λ,使 ,则A、B、C三点的位置关系如何?
思考7:如图,若P为AB的中点,则
与 、 的关系如何?
A
B
P
O
λ(xa±yb)=λxa±λyb.
思考8:向量的加、减、数乘运算统称为向量的线性运算,对于任意向量a、b,以及任意实数λ、x、y,λ(xa±yb)可转化为什么运算?
A
B
C
a
b
3b
2b
a
b
O
例2 如图,已知任意两个非零向量a, b,试作 =a+b, =a+2b,
=a+3b.你能判断A、B、C三点之间的位置关系吗?为什么?
思考:
例3 如图,平行四边形ABCD的两条对角线相交于点M,且 =a, =b,试用a,b表示向量 、 、 、
M
A B
D C
a
b
小结作业
1.实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
2.若λa=0,则可能有λ=0,也可能有a=0.
3.向量的数乘运算律,不是规定,而是可以证明的结论.向量共线定理是平面几何中证明三点共线,直线平行,线段数量关系的理论依据.
作业:
P90练习:3,4,5,6.
