数学:1.1.2《弧度制》课件
文档属性
| 名称 | 数学:1.1.2《弧度制》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-06 21:02:23 | ||
图片预览







文档简介
(共24张PPT)
【目标导学】
1、理解弧度制
2、掌握公式
3、掌握角度制与弧度制的换算
【主体自学】 看书P 6~8
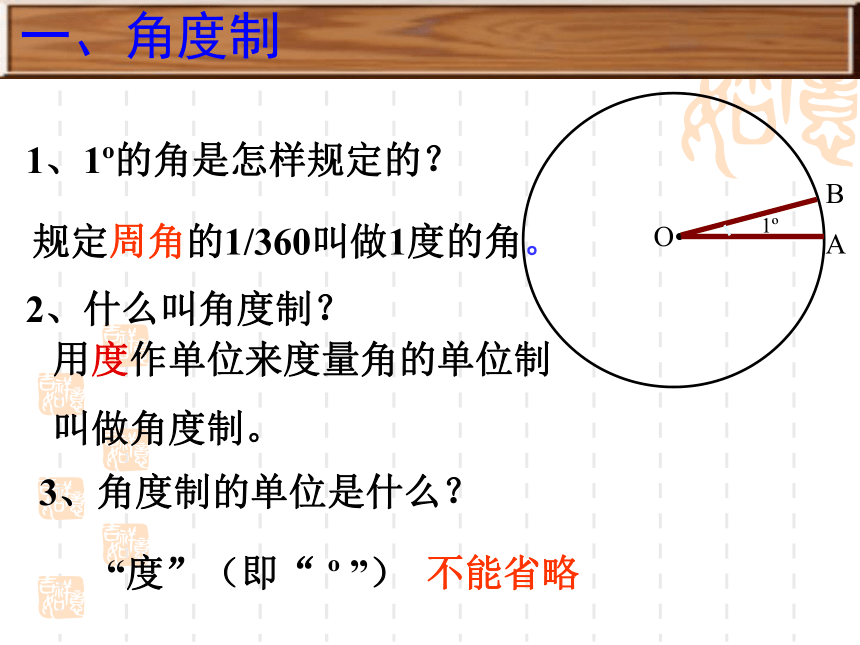
1、1 的角是怎样规定的?
2、什么叫角度制?
规定周角的1/360叫做1度的角。
用度作单位来度量角的单位制
叫做角度制。
O
A
B
1
3、角度制的单位是什么?
“度”(即“ ”) 不能省略
一、角度制
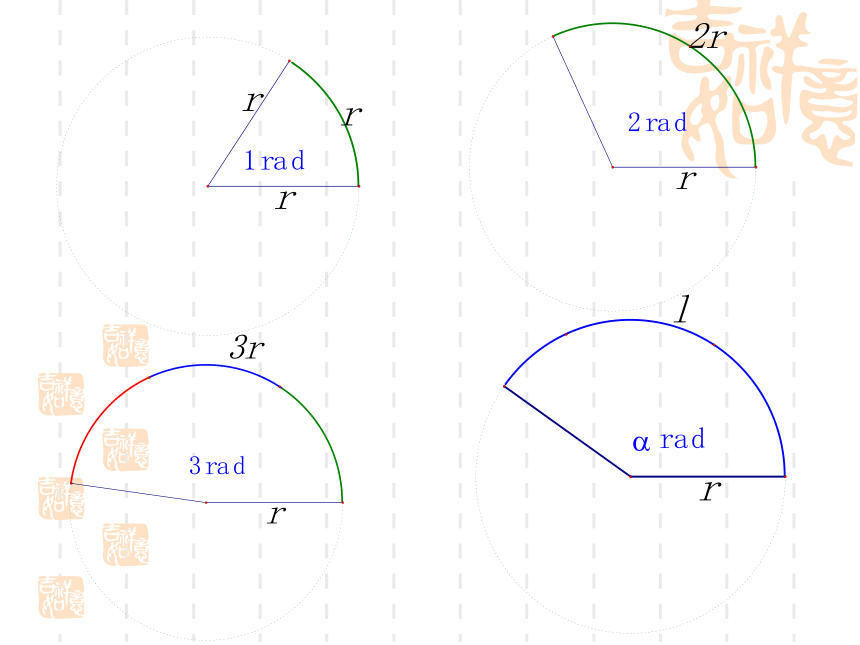
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。
r
r
二、弧度制
用符号rad表示,读作弧度。
这种用弧度作为单位度量角的单位制叫做弧度制。
弧度制的单位rad可以省略不写,如:1 rad可以写成1
探究:
(3)平角、周角的弧度数,(平角= rad、周角=2 rad)
⑵正角的弧度数是正数,负角的弧度数是负数,
零角的弧度数是0
(1)角 的弧度数的绝对值
(l为弧长,r为半径)
⑷用角度制和弧度制来度量零角,单位不同,
但数量相同(都是0), 用角度制和弧度制来度
量任一非零角,单位不同,量数也不同
三 角度制与弧度制的换算
1 把角度换成弧度
rad
2 把弧度换成角度
rad=360。
rad=180。
思考:弧度的大小是否与半径有关?为什么?
完成课本P 6 探究的表格
弧AB的长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的度数
?πr 逆时针方向 π 1800
2πr 逆时针 2π 3600
r 逆时针 1 57.30
2r 顺时针 -2 -114.60
πr 顺时针 - π -1800
0 未作旋转 0 00
πr 逆时针 π 1800
2πr 逆时针 2π 3600
角度
弧度
写出一些特殊角的弧度数
提示:应尽快熟悉和习惯弧度制!
把 化成弧度.
例1
解:∵
∴
角度制与弧度制互化时要抓住 弧度这个关键.
把 化成度.
例2
解:
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
的大小,而 是圆的 所对的圆心角(或该弧)
②1弧度是等于半径长的圆弧所对的圆心角(或该弧)
的大小;
③不论是以“弧度”还是以“度”为单位的角的大小都是一
个与圆的半径大小无关的定值.
正角
零角
负角
正实数
零
负实数
角的集合与实数集之间的一一对应关系:
例3利用弧度制证明下列关于扇形的公式
(1)
(2)
(3)
练习:已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( )
扇形面积是
小结
(1) 弧度;
将 乘以 ;
( 2)“角化弧”时,将 乘以 ;“弧化角”时,
(3)弧长公式:
对的弧长, 为圆心角的弧度数, 为圆半径.)
(其中 为圆心角 所
扇形面积公式:
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
弧长公式
换算关系
基本关系
导出关系
弧度制与角度制的比较:
1、角度制与弧度制:一一对应:
2、求弧长:
3、求扇形的面积:
正角
零角
负角
正实数
零
负实数
练习 P10 1~6
选做题:
(1)已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
(2)已知扇形周长为20 cm,当扇形的中心角为多大时它有最大面积?
【目标导学】
1、理解弧度制
2、掌握公式
3、掌握角度制与弧度制的换算
【主体自学】 看书P 6~8
1、1 的角是怎样规定的?
2、什么叫角度制?
规定周角的1/360叫做1度的角。
用度作单位来度量角的单位制
叫做角度制。
O
A
B
1
3、角度制的单位是什么?
“度”(即“ ”) 不能省略
一、角度制
我们把长度等于半径长的弧所对的圆心角叫做1弧度的角。
r
r
二、弧度制
用符号rad表示,读作弧度。
这种用弧度作为单位度量角的单位制叫做弧度制。
弧度制的单位rad可以省略不写,如:1 rad可以写成1
探究:
(3)平角、周角的弧度数,(平角= rad、周角=2 rad)
⑵正角的弧度数是正数,负角的弧度数是负数,
零角的弧度数是0
(1)角 的弧度数的绝对值
(l为弧长,r为半径)
⑷用角度制和弧度制来度量零角,单位不同,
但数量相同(都是0), 用角度制和弧度制来度
量任一非零角,单位不同,量数也不同
三 角度制与弧度制的换算
1 把角度换成弧度
rad
2 把弧度换成角度
rad=360。
rad=180。
思考:弧度的大小是否与半径有关?为什么?
完成课本P 6 探究的表格
弧AB的长 OB旋转的方向 ∠AOB的弧度数 ∠AOB的度数
?πr 逆时针方向 π 1800
2πr 逆时针 2π 3600
r 逆时针 1 57.30
2r 顺时针 -2 -114.60
πr 顺时针 - π -1800
0 未作旋转 0 00
πr 逆时针 π 1800
2πr 逆时针 2π 3600
角度
弧度
写出一些特殊角的弧度数
提示:应尽快熟悉和习惯弧度制!
把 化成弧度.
例1
解:∵
∴
角度制与弧度制互化时要抓住 弧度这个关键.
把 化成度.
例2
解:
角度制与弧度制的比较
①弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
的大小,而 是圆的 所对的圆心角(或该弧)
②1弧度是等于半径长的圆弧所对的圆心角(或该弧)
的大小;
③不论是以“弧度”还是以“度”为单位的角的大小都是一
个与圆的半径大小无关的定值.
正角
零角
负角
正实数
零
负实数
角的集合与实数集之间的一一对应关系:
例3利用弧度制证明下列关于扇形的公式
(1)
(2)
(3)
练习:已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
解:周长=2πR=2R+l,所以l=2(π-1)R.
所以扇形的中心角是2(π-1) rad.
合( )
扇形面积是
小结
(1) 弧度;
将 乘以 ;
( 2)“角化弧”时,将 乘以 ;“弧化角”时,
(3)弧长公式:
对的弧长, 为圆心角的弧度数, 为圆半径.)
(其中 为圆心角 所
扇形面积公式:
弧度制 角度制
度量单位 弧度(10进制) 度(60进制,1 =60,1′=60 )
单位规定 把长度等于半径长的弧所对的圆心角叫做1弧度的角。 周角的1/360叫做1度的角。
弧长公式
换算关系
基本关系
导出关系
弧度制与角度制的比较:
1、角度制与弧度制:一一对应:
2、求弧长:
3、求扇形的面积:
正角
零角
负角
正实数
零
负实数
练习 P10 1~6
选做题:
(1)已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
(2)已知扇形周长为20 cm,当扇形的中心角为多大时它有最大面积?
