苏科版九年级数学上册3.4《方差》同步练习(Word版 含答案)
文档属性
| 名称 | 苏科版九年级数学上册3.4《方差》同步练习(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 15:26:37 | ||
图片预览


文档简介
3.4 方差
一、选择题
1.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差是
( )
A.3
B.4
C.5
D.6
2.要从甲、乙、丙三名学生中选出一名学生参加数学竞赛,对这三名学生进行了10次数学测试,经过数据分析,3人的平均成绩均为92分,甲的方差为0.024,乙的方差为0.08,丙的方差为0.015,则这10次测试成绩比较稳定的是( )
A.甲
B.乙
C.丙
D.无法确定
3.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图1所示,对于这10名学生的参赛成绩,下列说法正确的是( )
图1
A.众数是90分
B.中位数是95分
C.平均数是95分
D.方差是15分2
4.如果一组数据6,7,x,9,5的平均数是2x,那么这组数据的方差为( )
A.4
B.3
C.2
D.1
5.若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A.4,3
B.6,3
C.3,4
D.6,5
二、填空题
6.数据0,1,1,x,3,4的极差是6,则x=________.
7.小米的爸爸为了了解她的数学成绩情况,现随机抽取她三次数学考试的成绩(单位:分),分别是87,93,90,则这三次数学成绩数据的方差是________.
8.一组数据2,x,1,3,5,4,若这组数据的中位数是3,则这组数据的方差是________.
9.两组数据m,n,6与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的方差是________.
10.一个样本的方差是s2=[(x1-20)2+(x2-20)2+…+(x10-20)2],则样本的个数为________,样本的平均数是________.
三、解答题
11.九(3)班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲组数据的中位数是________,乙组数据的众数是________;
(2)计算乙组数据的平均数和方差;
(3)已知甲组数据的方差是1.4,则成绩较为整齐的是________.
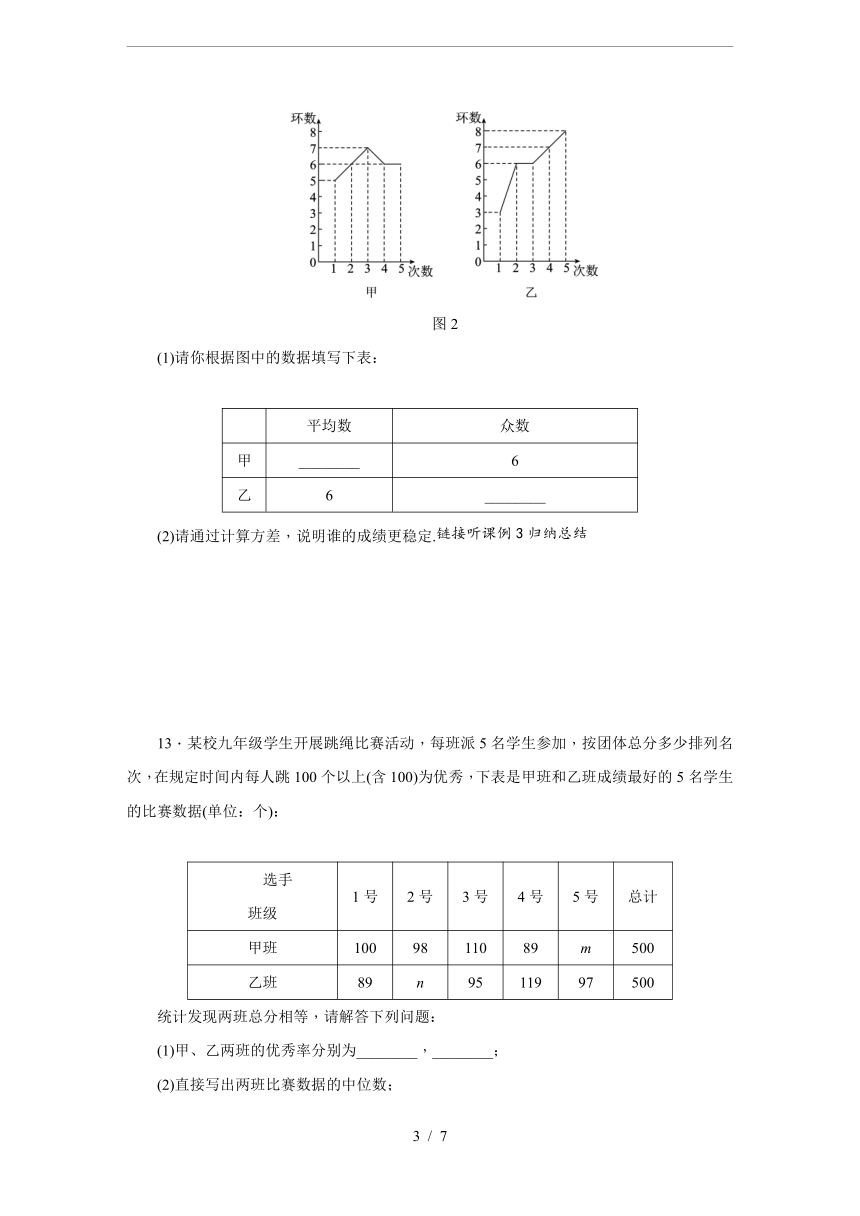
12.甲、乙两人在相同的条件下各射击5次,每次射击的成绩情况如图2.
图2
(1)请你根据图中的数据填写下表:
平均数
众数
甲
________
6
乙
6
________
(2)请通过计算方差,说明谁的成绩更稳定.
13.某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100)为优秀,下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个):
选手
班级
1号
2号
3号
4号
5号
总计
甲班
100
98
110
89
m
500
乙班
89
n
95
119
97
500
统计发现两班总分相等,请解答下列问题:
(1)甲、乙两班的优秀率分别为________,________;
(2)直接写出两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
14.某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射击5次,成绩统计如表:
命中环数
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
(1)根据上述信息可知:甲命中环数的中位数是________环,乙命中环数的众数是________环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定;
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会________(填“变大”“变小”或“不变”).
15某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算出了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
(1)a=________;
(2)请完成图3中表示乙成绩变化情况的折线;
(3)观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
小宇的作业:
解:x甲=×(9+4+7+4+6)=6(环),
s甲2=×[(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]=×(9+4+1+4+0)=3.6(环2).
图3
答案
1.B
2.
C.
3.A.
4.
A.
5.
B.
6.
x=6或x=-2.
7.6.
8.
.
9.
6.
10.10 20
11.解:(1)x甲=×(5+6+7+6+6)=6,
乙的5次射击中,有2次为6环,出现次数最多,
故众数为6环.
(2)s甲2=×[(5-6)2+(6-6)2+(7-6)2+(6-6)2+(6-6)2]=(环2),
s乙2=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=(环2).
∵<,∴甲成绩的方差比乙成绩的方差小,∴甲的成绩更稳定.
12.解:(1)m=500-100-98-110-89=103,n=500-89-95-119-97=100,
甲班的优秀率==60%,乙班的优秀率==40%.故答案为60%,40%.
(2)甲班比赛数据的中位数为100,乙班比赛数据的中位数为97.
(3)x甲=x乙=500÷5=100,s甲2=×[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,
s乙2=×[(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2.
(4)甲为冠军.理由:甲、乙两班的平均数相同,甲班的方差小于乙班的方差,所以甲班成绩稳定,故甲为冠军.
13.解:(1)8 6和9
(2)甲的平均数是(7+8×3+9)÷5=8,
则甲的方差是×[(7-8)2+3×(8-8)2+(9-8)2]=0.4,
乙的平均数是(6×2+9×2+10)÷5=8,
则甲的方差是×[2×(6-8)2+2×(9-8)2+(10-8)2]=2.8,
因为0.4<2.8.所以甲的成绩比较稳定.
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差变小.
故答案为变小.
15
解:(1)甲的总成绩是9+4+7+4+6=30(环),
则a=30-7-7-5-7=4.
故答案为4.
(2)如图所示:
(3)观察图,可看出乙的成绩比较稳定.
∵x乙=30÷5=6(环),
∴s乙2=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(7-6)2]=1.6(环2).
∵s甲2>s乙2,∴上述判断正确.
/
一、选择题
1.已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差是
( )
A.3
B.4
C.5
D.6
2.要从甲、乙、丙三名学生中选出一名学生参加数学竞赛,对这三名学生进行了10次数学测试,经过数据分析,3人的平均成绩均为92分,甲的方差为0.024,乙的方差为0.08,丙的方差为0.015,则这10次测试成绩比较稳定的是( )
A.甲
B.乙
C.丙
D.无法确定
3.在“经典诵读”比赛活动中,某校10名学生参赛成绩如图1所示,对于这10名学生的参赛成绩,下列说法正确的是( )
图1
A.众数是90分
B.中位数是95分
C.平均数是95分
D.方差是15分2
4.如果一组数据6,7,x,9,5的平均数是2x,那么这组数据的方差为( )
A.4
B.3
C.2
D.1
5.若一组数据a1,a2,a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )
A.4,3
B.6,3
C.3,4
D.6,5
二、填空题
6.数据0,1,1,x,3,4的极差是6,则x=________.
7.小米的爸爸为了了解她的数学成绩情况,现随机抽取她三次数学考试的成绩(单位:分),分别是87,93,90,则这三次数学成绩数据的方差是________.
8.一组数据2,x,1,3,5,4,若这组数据的中位数是3,则这组数据的方差是________.
9.两组数据m,n,6与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的方差是________.
10.一个样本的方差是s2=[(x1-20)2+(x2-20)2+…+(x10-20)2],则样本的个数为________,样本的平均数是________.
三、解答题
11.九(3)班组织了一次经典诵读比赛,甲、乙两组各10人的比赛成绩如下表(10分制):
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)甲组数据的中位数是________,乙组数据的众数是________;
(2)计算乙组数据的平均数和方差;
(3)已知甲组数据的方差是1.4,则成绩较为整齐的是________.
12.甲、乙两人在相同的条件下各射击5次,每次射击的成绩情况如图2.
图2
(1)请你根据图中的数据填写下表:
平均数
众数
甲
________
6
乙
6
________
(2)请通过计算方差,说明谁的成绩更稳定.
13.某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100)为优秀,下表是甲班和乙班成绩最好的5名学生的比赛数据(单位:个):
选手
班级
1号
2号
3号
4号
5号
总计
甲班
100
98
110
89
m
500
乙班
89
n
95
119
97
500
统计发现两班总分相等,请解答下列问题:
(1)甲、乙两班的优秀率分别为________,________;
(2)直接写出两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
14.某射击队教练为了了解队员的训练情况,从队员中选取甲、乙两名队员进行射击测试,相同条件下各射击5次,成绩统计如表:
命中环数
6
7
8
9
10
甲命中相应环数的次数
0
1
3
1
0
乙命中相应环数的次数
2
0
0
2
1
(1)根据上述信息可知:甲命中环数的中位数是________环,乙命中环数的众数是________环;
(2)试通过计算说明甲、乙两人的成绩谁比较稳定;
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差会________(填“变大”“变小”或“不变”).
15某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算出了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
(1)a=________;
(2)请完成图3中表示乙成绩变化情况的折线;
(3)观察图,可看出________的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
小宇的作业:
解:x甲=×(9+4+7+4+6)=6(环),
s甲2=×[(9-6)2+(4-6)2+(7-6)2+(4-6)2+(6-6)2]=×(9+4+1+4+0)=3.6(环2).
图3
答案
1.B
2.
C.
3.A.
4.
A.
5.
B.
6.
x=6或x=-2.
7.6.
8.
.
9.
6.
10.10 20
11.解:(1)x甲=×(5+6+7+6+6)=6,
乙的5次射击中,有2次为6环,出现次数最多,
故众数为6环.
(2)s甲2=×[(5-6)2+(6-6)2+(7-6)2+(6-6)2+(6-6)2]=(环2),
s乙2=×[(3-6)2+(6-6)2+(6-6)2+(7-6)2+(8-6)2]=(环2).
∵<,∴甲成绩的方差比乙成绩的方差小,∴甲的成绩更稳定.
12.解:(1)m=500-100-98-110-89=103,n=500-89-95-119-97=100,
甲班的优秀率==60%,乙班的优秀率==40%.故答案为60%,40%.
(2)甲班比赛数据的中位数为100,乙班比赛数据的中位数为97.
(3)x甲=x乙=500÷5=100,s甲2=×[(100-100)2+(98-100)2+(110-100)2+(89-100)2+(103-100)2]=46.8,
s乙2=×[(89-100)2+(100-100)2+(95-100)2+(119-100)2+(97-100)2]=103.2.
(4)甲为冠军.理由:甲、乙两班的平均数相同,甲班的方差小于乙班的方差,所以甲班成绩稳定,故甲为冠军.
13.解:(1)8 6和9
(2)甲的平均数是(7+8×3+9)÷5=8,
则甲的方差是×[(7-8)2+3×(8-8)2+(9-8)2]=0.4,
乙的平均数是(6×2+9×2+10)÷5=8,
则甲的方差是×[2×(6-8)2+2×(9-8)2+(10-8)2]=2.8,
因为0.4<2.8.所以甲的成绩比较稳定.
(3)如果乙再射击1次,命中8环,那么乙射击成绩的方差变小.
故答案为变小.
15
解:(1)甲的总成绩是9+4+7+4+6=30(环),
则a=30-7-7-5-7=4.
故答案为4.
(2)如图所示:
(3)观察图,可看出乙的成绩比较稳定.
∵x乙=30÷5=6(环),
∴s乙2=×[(7-6)2+(5-6)2+(7-6)2+(4-6)2+(7-6)2]=1.6(环2).
∵s甲2>s乙2,∴上述判断正确.
/
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
