人教版数学八年级上册 12.3 角的平分线的性质 同步练习(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级上册 12.3 角的平分线的性质 同步练习(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 173.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-26 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
12.3
角的平分线的性质
一、选择题
1.已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M(??
)
A.?在AC边的高上????????B.?在AC边的中线上????????C.?在∠ABC的平分线上????????D.?在AC边的垂直平分线上
2.如图,
平分
,
,
,垂足分别为
、
,若
,则
(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
3.如图,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=12,DF=2,AC=3,则AB的长是(??
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?7???????????????????????????????????????????D.?9
4.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(????
)
A.?△ABC的三条中线的交点?????????????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点??????????????????????????????????D.?△ABC三条高所在直线的交点
5.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)
∠APB=90°-∠O,其中正确的有(
???)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
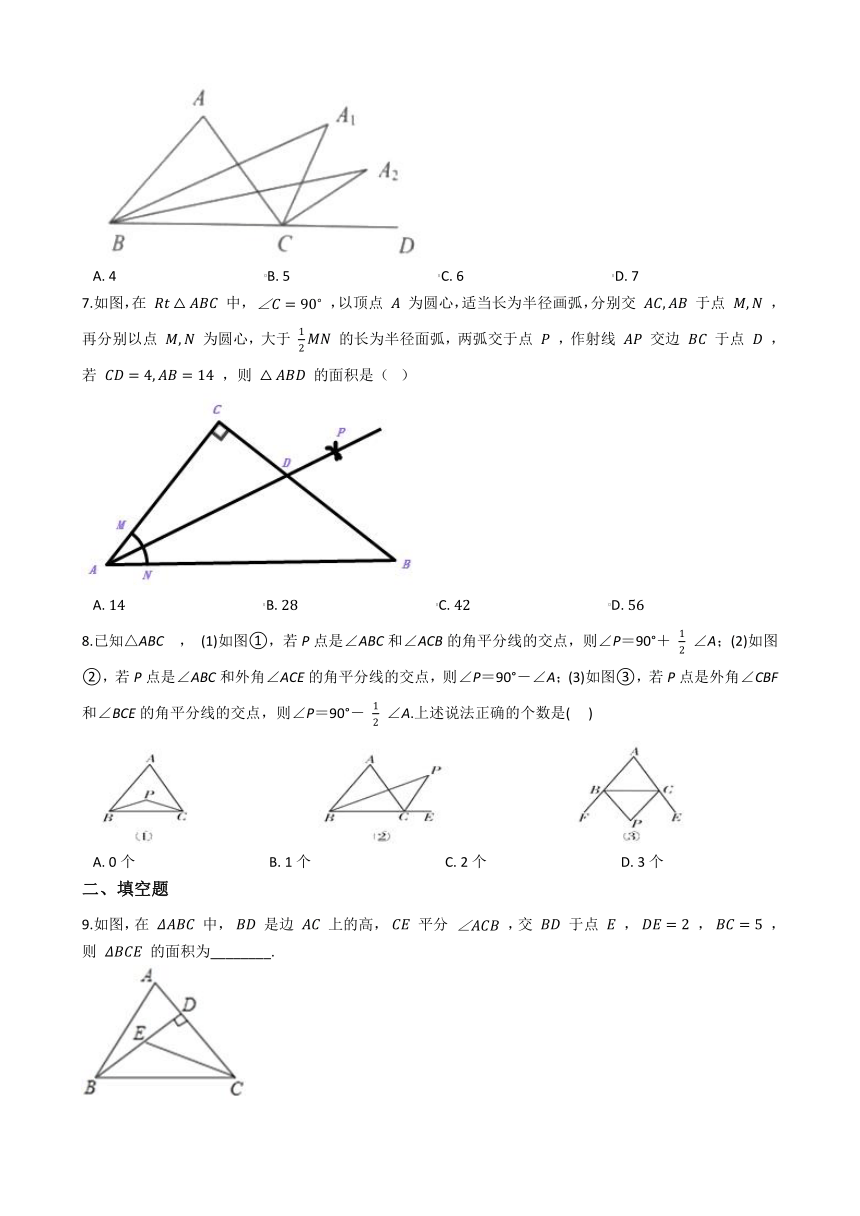
6.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1
,
得∠A1;∠A1BC与∠A1CD的平分线相交于点A2
,
得∠A2;……:∠An-1BC与∠An-1CD的平分线交于点An
,
要使∠An的度数为整数,则n的最大值为(???
)
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
7.如图,在
中,
,以顶点
为圆心,适当长为半径画弧,分别交
于点
,再分别以点
为圆心,大于
的长为半径面弧,两弧交于点
,作射线
交边
于点
,若
,则
的面积是(?
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
8.已知△ABC
,
(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A.上述说法正确的个数是(???
)
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
二、填空题
9.如图,在
中,
是边
上的高,
平分
,交
于点
,
,
,则
的面积为________.
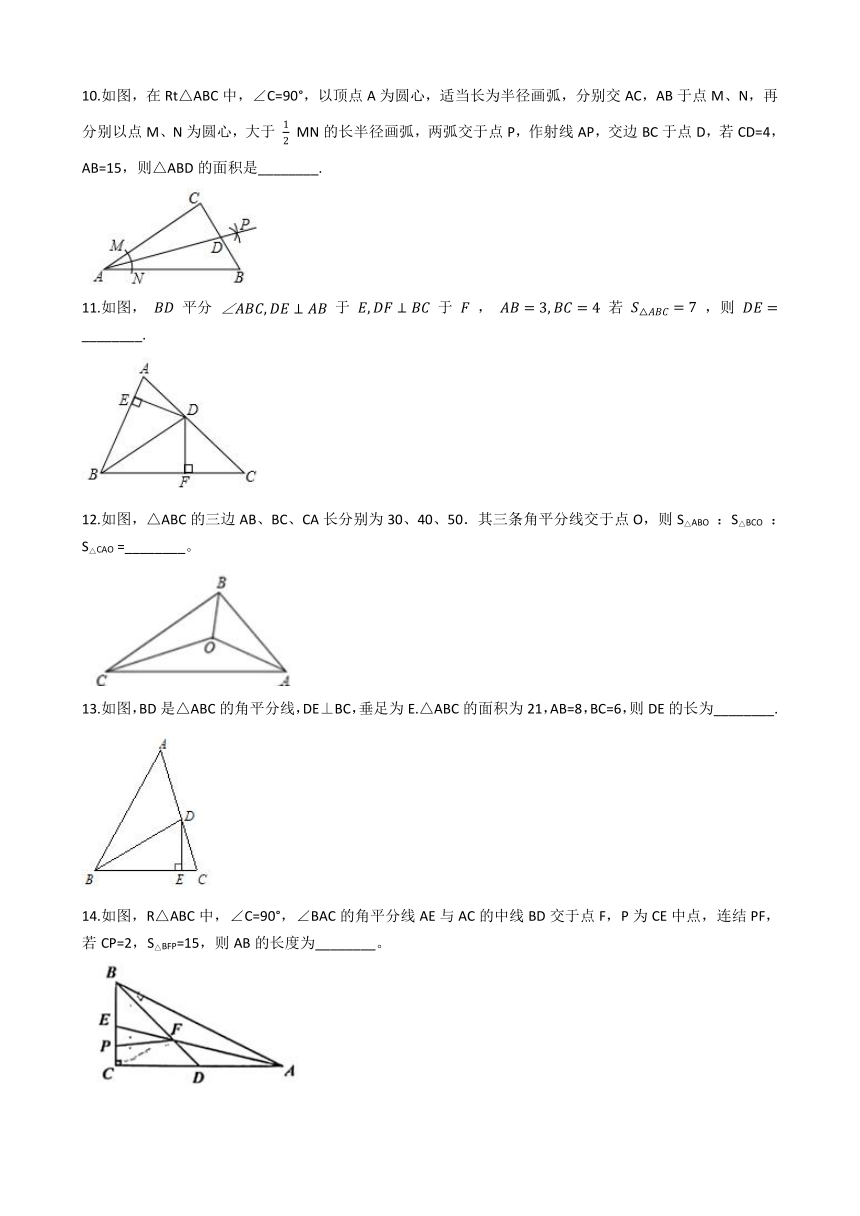
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于
MN的长半径画弧,两弧交于点P,作射线AP,交边BC于点D,若CD=4,AB=15,则△ABD的面积是________.
11.如图,
平分
于
于
,
若
,则
________.
12.如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO
:S△BCO
:S△CAO
=________。
13.如图,BD是△ABC的角平分线,DE⊥BC,垂足为E.△ABC的面积为21,AB=8,BC=6,则DE的长为________.
14.如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为________。
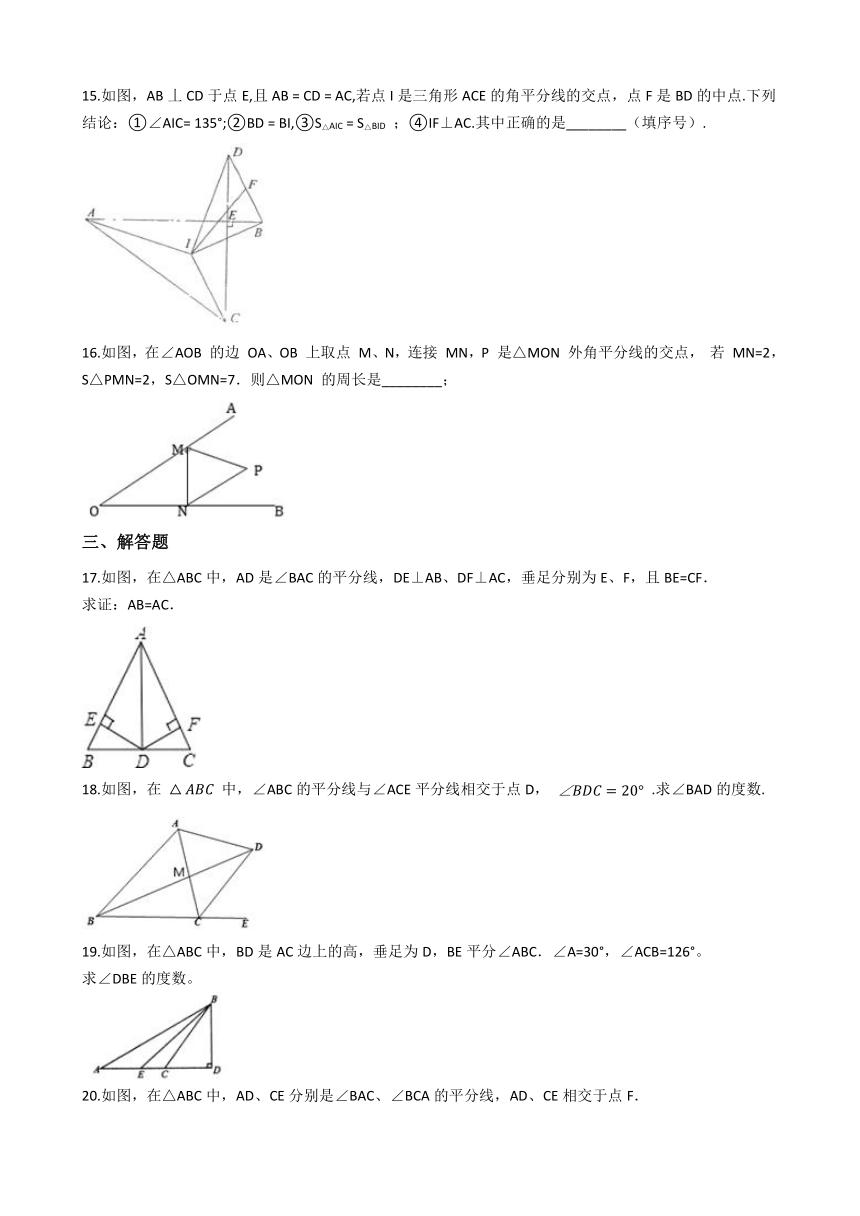
15.如图,AB丄CD于点E,且AB
=
CD
=
AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=
135°;②BD
=
BI,③S△AIC
=
S△BID
;④IF⊥AC.其中正确的是________(填序号).
16.如图,在∠AOB
的边
OA、OB
上取点
M、N,连接
MN,P
是△MON
外角平分线的交点,
若
MN=2,S△PMN=2,S△OMN=7.则△MON
的周长是________;
三、解答题
17.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB、DF⊥AC,垂足分别为E、F,且BE=CF.
求证:AB=AC.
18.如图,在
中,∠ABC的平分线与∠ACE平分线相交于点D,
.求∠BAD的度数.
19.如图,在△ABC中,BD是AC边上的高,垂足为D,BE平分∠ABC.∠A=30°,∠ACB=126°。
求∠DBE的度数。
20.如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)求证:∠EFA=90°-
∠B;
(2)若∠B=60°,求证:EF=DF.
21.如图(a),∠DAB+∠ABC+∠BCE=360°
(1)求证:AD∥CE
(2)如图(b),AG、CG分别平分∠BAD、∠BCE,BF∥AG交GC的延长线于F,判断∠ABC与∠F的数量关系,并证明;
(3)如图(c),AN平分∠HAB,BP平分∠ABC,BQ∥AN,CM平分∠BCT交BQ的反向延长线于M,①
的值不变,②
的值不变;其中只有一个结论正确,请择一证明.
答案
一、选择题
1.
C
2.
B
3.
D
4.
C
5.
C
6.
C
7.
B
8.
C
二、填空题
9.
5
10.
30
11.
2
12.
3:4:5
13.
3
14.
15
15.
①
16.
11
三、解答题
17.证明:∵AD平分∠EAD,DE⊥AB,DF⊥AC,
∴DE=DF,
∵在Rt△AED与Rt△AFD中,
,
∴△AED≌△AFD,
∴AE=AF,
∵BE=CF,
∴AB=AC.
18.
∵∠ABC的平分线BM与△ACB的外角∠ACE的平分线CD相交于点D,
∴∠DCE=
∠ACE,∠DBC=
∠ABC,
∵∠DCE是△BCD的外角,
∴∠BDC=∠DCE-∠DBC=
∠ACE-
∠ABC=
(∠BAC+∠ABC)-
∠ABC=
(∠BAC+
∠ABC-
∠ABC)=
∠BAC,
∵∠BDC=20°,
∴∠BAC=2×20°=40°,
过D点分别作DE⊥BE交于E点,DG⊥AC交于G点,DF⊥BF交BA的延长线于F点,
∵BD平分∠ABC,CD平分∠ACE,
∴DE=DF,DE=DG,
∴DF
=DG;
在Rt△DGA与Rt△DFA中,
∵DF
=DG,DA=DA,
∴Rt△DGA≌Rt△DFA(HL),
∴∠DAG=∠DAF,
又∵∠BAC=40°,
∴∠CAF=140°,
∴∠CAD=70°,
∴∠BAD=∠BAC+∠CAD
=110°.
19.
解:在△ABC中,∵∠A=30°,∠ACB=126°,
∴∠ABC=180°-∠A-∠ACB=24°,
∵BE平分∠ABC,∴∠ABE=
∠ABC=12°,
∵BD是AC边上的高,∴∠ADB=90°,
在Rt△ADB中,∠ABD=90°-∠A=60°,
∴∠DBE=∠ABD-∠ABE=48°,故∠DBE的度数是48°.
20.
(1)证明:∵∠BAC+∠BCA=180°-∠B,
又∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=
∠BAC,∠FCA=
∠BCA,
∴∠FAC+∠FCA=
×(180°-∠B)=90°-
∠B,
∵∠EFA=∠FAC+∠FCA,
∴∠EFA=90°-
∠B.
(2)证明:如图,过点F作FG⊥BC于G,作FH⊥AB于H,作FM⊥AC于M.
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FM,
∵∠EFH+∠DFH=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG,
在△EFH和△DFG中,
,
∴△EFH≌△DFG(AAS),
∴EF=DF.
21.
(1)解:过B作BF∥AD,
则∠DAB+∠ABF=180°,
∵∠DAB+∠ABC+∠BCE=360°,
∴∠FBC+∠BCE=360°﹣180°=180°,
∴BF∥CE,
∴AD∥CE.
(2)解:∠ABC=2∠F
证明:过点G作GH∥AD,
则GH∥AD∥CE,
∴∠DAG=∠AGH,∠HGC=∠GCE,
∵AG、CG分别平分∠BAD、∠BCE,
∴∠AGC=
(∠DAB+∠BCE),
∵∠DAB+∠ABC+∠BCE=360°,
∴
(∠DAB+∠ABC+∠BCE)=180°,
即∠AGC+
∠ABC=180°,
∵AG∥BF,
∴∠F+∠AGC=180°,
∴∠ABC=2∠F.
(3)解:②
的值不变.
证明:由上面结论可得,∠ABC=∠HAB+∠TCB,
又∵AN平分∠HAB,BP平分∠ABC,CM平分∠BCT,
∴∠ABP=∠NAB+∠MCB,
∵BQ∥AN,
∴∠NAB=∠ABQ,
∴∠QBP=
∠ABP=
∠CBP=
∠BCT=∠MCB,
∵∠QBC是△BCM的外角,
∴∠QBC=∠M+∠MCB,
∴∠M=∠QBC﹣∠MCB=∠QBC﹣∠QBP=∠PBC=
∠ABC,
即
的值为
.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
12.3
角的平分线的性质
一、选择题
1.已知△ABC内一点M,如果点M到两边AB、BC的距离相等,那么点M(??
)
A.?在AC边的高上????????B.?在AC边的中线上????????C.?在∠ABC的平分线上????????D.?在AC边的垂直平分线上
2.如图,
平分
,
,
,垂足分别为
、
,若
,则
(???
)
A.??????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?
3.如图,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=12,DF=2,AC=3,则AB的长是(??
)
A.?2???????????????????????????????????????????B.?4???????????????????????????????????????????C.?7???????????????????????????????????????????D.?9
4.现要在一块三角形的草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(????
)
A.?△ABC的三条中线的交点?????????????????????????????????????B.?△ABC三边的垂直平分线的交点
C.?△ABC三条角平分线的交点??????????????????????????????????D.?△ABC三条高所在直线的交点
5.如图,△AOB的外角∠CAB,∠DBA的平分线AP,BP相交于点P,PE⊥OC于E,PF⊥OD于F,下列结论:(1)PE=PF;(2)点P在∠COD的平分线上;(3)
∠APB=90°-∠O,其中正确的有(
???)
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
6.如图,在△ABC中,∠A=64°,∠ABC与∠ACD的平分线交于点A1
,
得∠A1;∠A1BC与∠A1CD的平分线相交于点A2
,
得∠A2;……:∠An-1BC与∠An-1CD的平分线交于点An
,
要使∠An的度数为整数,则n的最大值为(???
)
A.?4???????????????????????????????????????????B.?5???????????????????????????????????????????C.?6???????????????????????????????????????????D.?7
7.如图,在
中,
,以顶点
为圆心,适当长为半径画弧,分别交
于点
,再分别以点
为圆心,大于
的长为半径面弧,两弧交于点
,作射线
交边
于点
,若
,则
的面积是(?
)
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?
8.已知△ABC
,
(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A.上述说法正确的个数是(???
)
?
A.?0个???????????????????????????????????????B.?1个???????????????????????????????????????C.?2个???????????????????????????????????????D.?3个
二、填空题
9.如图,在
中,
是边
上的高,
平分
,交
于点
,
,
,则
的面积为________.
10.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于
MN的长半径画弧,两弧交于点P,作射线AP,交边BC于点D,若CD=4,AB=15,则△ABD的面积是________.
11.如图,
平分
于
于
,
若
,则
________.
12.如图,△ABC的三边AB、BC、CA长分别为30、40、50.其三条角平分线交于点O,则S△ABO
:S△BCO
:S△CAO
=________。
13.如图,BD是△ABC的角平分线,DE⊥BC,垂足为E.△ABC的面积为21,AB=8,BC=6,则DE的长为________.
14.如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为________。
15.如图,AB丄CD于点E,且AB
=
CD
=
AC,若点I是三角形ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=
135°;②BD
=
BI,③S△AIC
=
S△BID
;④IF⊥AC.其中正确的是________(填序号).
16.如图,在∠AOB
的边
OA、OB
上取点
M、N,连接
MN,P
是△MON
外角平分线的交点,
若
MN=2,S△PMN=2,S△OMN=7.则△MON
的周长是________;
三、解答题
17.如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB、DF⊥AC,垂足分别为E、F,且BE=CF.
求证:AB=AC.
18.如图,在
中,∠ABC的平分线与∠ACE平分线相交于点D,
.求∠BAD的度数.
19.如图,在△ABC中,BD是AC边上的高,垂足为D,BE平分∠ABC.∠A=30°,∠ACB=126°。
求∠DBE的度数。
20.如图,在△ABC中,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
(1)求证:∠EFA=90°-
∠B;
(2)若∠B=60°,求证:EF=DF.
21.如图(a),∠DAB+∠ABC+∠BCE=360°
(1)求证:AD∥CE
(2)如图(b),AG、CG分别平分∠BAD、∠BCE,BF∥AG交GC的延长线于F,判断∠ABC与∠F的数量关系,并证明;
(3)如图(c),AN平分∠HAB,BP平分∠ABC,BQ∥AN,CM平分∠BCT交BQ的反向延长线于M,①
的值不变,②
的值不变;其中只有一个结论正确,请择一证明.
答案
一、选择题
1.
C
2.
B
3.
D
4.
C
5.
C
6.
C
7.
B
8.
C
二、填空题
9.
5
10.
30
11.
2
12.
3:4:5
13.
3
14.
15
15.
①
16.
11
三、解答题
17.证明:∵AD平分∠EAD,DE⊥AB,DF⊥AC,
∴DE=DF,
∵在Rt△AED与Rt△AFD中,
,
∴△AED≌△AFD,
∴AE=AF,
∵BE=CF,
∴AB=AC.
18.
∵∠ABC的平分线BM与△ACB的外角∠ACE的平分线CD相交于点D,
∴∠DCE=
∠ACE,∠DBC=
∠ABC,
∵∠DCE是△BCD的外角,
∴∠BDC=∠DCE-∠DBC=
∠ACE-
∠ABC=
(∠BAC+∠ABC)-
∠ABC=
(∠BAC+
∠ABC-
∠ABC)=
∠BAC,
∵∠BDC=20°,
∴∠BAC=2×20°=40°,
过D点分别作DE⊥BE交于E点,DG⊥AC交于G点,DF⊥BF交BA的延长线于F点,
∵BD平分∠ABC,CD平分∠ACE,
∴DE=DF,DE=DG,
∴DF
=DG;
在Rt△DGA与Rt△DFA中,
∵DF
=DG,DA=DA,
∴Rt△DGA≌Rt△DFA(HL),
∴∠DAG=∠DAF,
又∵∠BAC=40°,
∴∠CAF=140°,
∴∠CAD=70°,
∴∠BAD=∠BAC+∠CAD
=110°.
19.
解:在△ABC中,∵∠A=30°,∠ACB=126°,
∴∠ABC=180°-∠A-∠ACB=24°,
∵BE平分∠ABC,∴∠ABE=
∠ABC=12°,
∵BD是AC边上的高,∴∠ADB=90°,
在Rt△ADB中,∠ABD=90°-∠A=60°,
∴∠DBE=∠ABD-∠ABE=48°,故∠DBE的度数是48°.
20.
(1)证明:∵∠BAC+∠BCA=180°-∠B,
又∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠FAC=
∠BAC,∠FCA=
∠BCA,
∴∠FAC+∠FCA=
×(180°-∠B)=90°-
∠B,
∵∠EFA=∠FAC+∠FCA,
∴∠EFA=90°-
∠B.
(2)证明:如图,过点F作FG⊥BC于G,作FH⊥AB于H,作FM⊥AC于M.
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FM,
∵∠EFH+∠DFH=120°,
∠DFG+∠DFH=360°-90°×2-60°=120°,
∴∠EFH=∠DFG,
在△EFH和△DFG中,
,
∴△EFH≌△DFG(AAS),
∴EF=DF.
21.
(1)解:过B作BF∥AD,
则∠DAB+∠ABF=180°,
∵∠DAB+∠ABC+∠BCE=360°,
∴∠FBC+∠BCE=360°﹣180°=180°,
∴BF∥CE,
∴AD∥CE.
(2)解:∠ABC=2∠F
证明:过点G作GH∥AD,
则GH∥AD∥CE,
∴∠DAG=∠AGH,∠HGC=∠GCE,
∵AG、CG分别平分∠BAD、∠BCE,
∴∠AGC=
(∠DAB+∠BCE),
∵∠DAB+∠ABC+∠BCE=360°,
∴
(∠DAB+∠ABC+∠BCE)=180°,
即∠AGC+
∠ABC=180°,
∵AG∥BF,
∴∠F+∠AGC=180°,
∴∠ABC=2∠F.
(3)解:②
的值不变.
证明:由上面结论可得,∠ABC=∠HAB+∠TCB,
又∵AN平分∠HAB,BP平分∠ABC,CM平分∠BCT,
∴∠ABP=∠NAB+∠MCB,
∵BQ∥AN,
∴∠NAB=∠ABQ,
∴∠QBP=
∠ABP=
∠CBP=
∠BCT=∠MCB,
∵∠QBC是△BCM的外角,
∴∠QBC=∠M+∠MCB,
∴∠M=∠QBC﹣∠MCB=∠QBC﹣∠QBP=∠PBC=
∠ABC,
即
的值为
.
