人教版七年级上册数学 1.2.2数轴课件(共15张PPT)
文档属性
| 名称 | 人教版七年级上册数学 1.2.2数轴课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 21:14:19 | ||
图片预览




文档简介
1.2.2 数轴
1.观察下面的温度计,读出温度,分别是:
____°C、 ____°C、 ____°C.
创设情境 温故探新
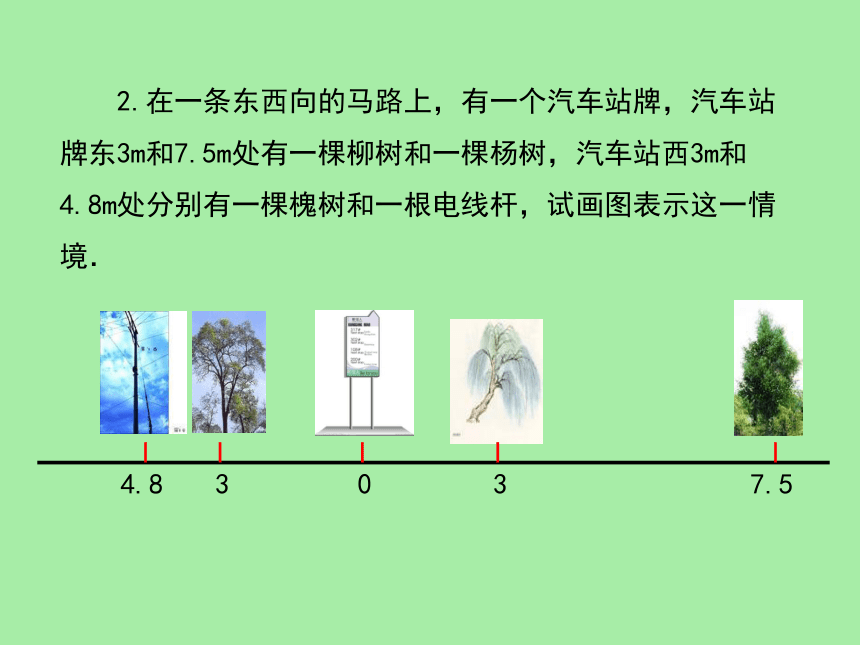
2.在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
0
-3 -2 -1 1 2 3
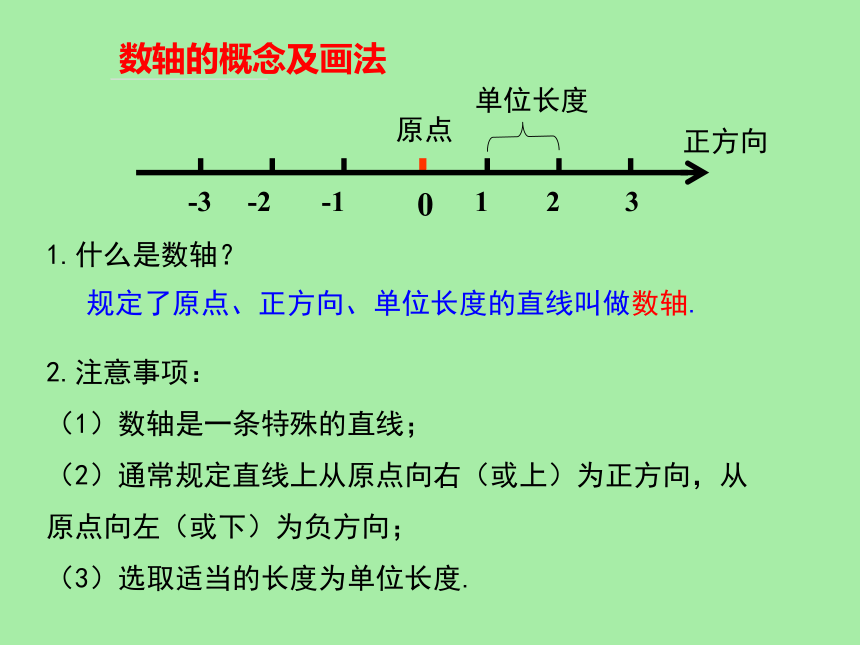
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
数轴的概念及画法
0
-3 -2 -1 1 2 3
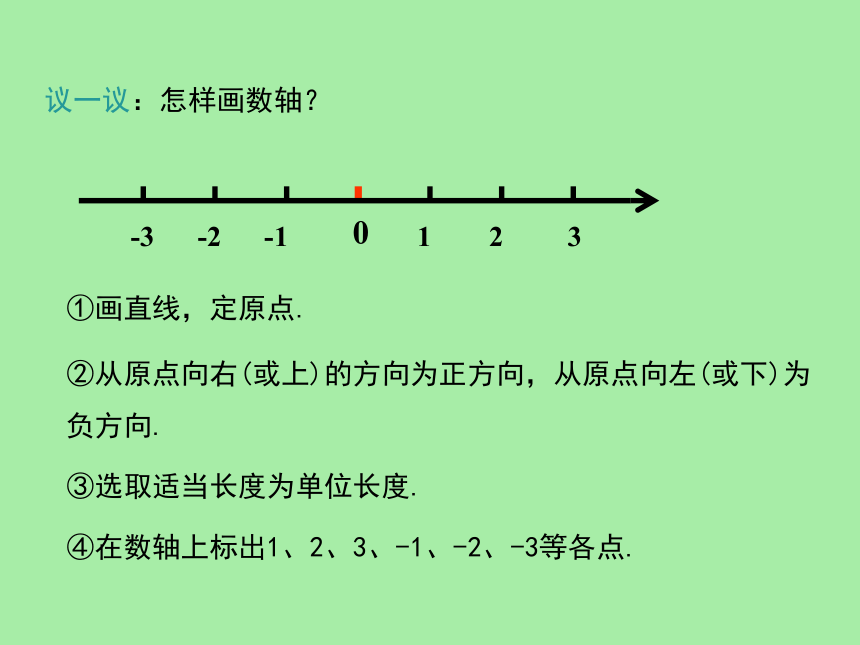
议一议:怎样画数轴?
④在数轴上标出1、2、3、-1、-2、-3等各点.
①画直线,定原点.
②从原点向右(或上)的方向为正方向,从原点向左(或下)为负方向.
③选取适当长度为单位长度.
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
a
左
0
1 2
-2 -1
例2 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
(4) D点表示-1.5
(1)A 点表示2;
(2) B 点表示0.25;
(3)C点表示-0.75;
解:
.
.
.
.
(1)
(2)
(3)
(4)
1.下列各图是数轴吗?说明你的理由.
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
-3 -2 -1 1 2 3
0
0
×
×
×
×
巩固新知
2.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
3. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界限.
课堂小结
再见,谢谢大家!
1.观察下面的温度计,读出温度,分别是:
____°C、 ____°C、 ____°C.
创设情境 温故探新
2.在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
0
3
7.5
3
4.8
0
-3 -2 -1 1 2 3
1.什么是数轴?
原点
正方向
单位长度
规定了原点、正方向、单位长度的直线叫做数轴.
2.注意事项:
(1)数轴是一条特殊的直线;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度.
数轴的概念及画法
0
-3 -2 -1 1 2 3
议一议:怎样画数轴?
④在数轴上标出1、2、3、-1、-2、-3等各点.
①画直线,定原点.
②从原点向右(或上)的方向为正方向,从原点向左(或下)为负方向.
③选取适当长度为单位长度.
观察下列图形,指出哪条数轴画得正确,其余错在哪里?
1
2
3
A
0
1
-1
2
B
1
0
1
-1
-2
2
E
-1
0
D
-2
-2
0
2
-4
-6
4
C
6
0
-3 -2 -1 1 2 3
思考:
3.如何用数轴上的点来表示分数或小数?
如:1.5,- — 怎样表示.
2
3
.
.
在数轴上表示有理数
1.观察上面数轴,哪些数在原点的左边,哪些数在原点的右边,由此你有什么发现?
2.每个数到原点的距离是多少?由此你又有什么发现?
例1 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看.
4
任何一个有理数都可以用数轴上的一个点来表示.
一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
a
左
0
1 2
-2 -1
例2 在下面数轴上,A,B,C,D各点分别表示什么数?
D C B A
(4) D点表示-1.5
(1)A 点表示2;
(2) B 点表示0.25;
(3)C点表示-0.75;
解:
.
.
.
.
(1)
(2)
(3)
(4)
1.下列各图是数轴吗?说明你的理由.
0
-3 -2 -1 1 2 3
-3 -2 -1 1 2 3 4
-3 -2 -1 1 2 3
0
0
×
×
×
×
巩固新知
2.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是
0,-2,1,2.5,-3.
3. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
1.数轴的定义:规定了原点、正方向和单位长度的直线叫数轴.
2.数轴的画法.
3.所有的有理数都可以用数轴上的点来表示,原点右边的数是正数,原点左边的数是负数,0是正负数的分界限.
课堂小结
再见,谢谢大家!
