人教版数学五年级上册6.3 梯形的面积 教案
文档属性
| 名称 | 人教版数学五年级上册6.3 梯形的面积 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 80.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 06:47:08 | ||
图片预览

文档简介
第3课时 梯形的面积
教学目标 1.理解和掌握梯形的面积计算公式,能运用公式正确地计算梯形的面积,并能运用公式解决实际问题。
2.理解梯形面积计算公式的推导过程,培养学生的自我探索精神。
3.提高学生运用知识解决问题的能力,培养分析概括和思考的能力。
重点难点 重点:理解并掌握梯形的面积计算公式,能运用公式解决实际问题。
难点:理解梯形面积计算公式的推导过程。
教学内容 对应教材第95页内容,第96页例3、“做一做”和第97~98页“练习二十一”的第1、2、5、6题。
教学准备 教具准备:PPT课件
教学过程
教学环节 教案设计 二次备课
回顾旧知 引入新课
(5分钟) 1.回顾以前所学知识,完成下列填空。
(1)梯形有( )条边,它的对边( )。
(2)平行四边形的面积=( )×( )
三角形的面积=( )×( )÷( )
2.引出课题,明确本节课的学习内容。
我们身边有很多物品的形状是梯形,如小汽车的车窗,你能用学过的方法推导出梯形的面积计算公式吗?这节课我们来研究梯形的面积。
创设情境
自主探究(20分钟)
创设情境
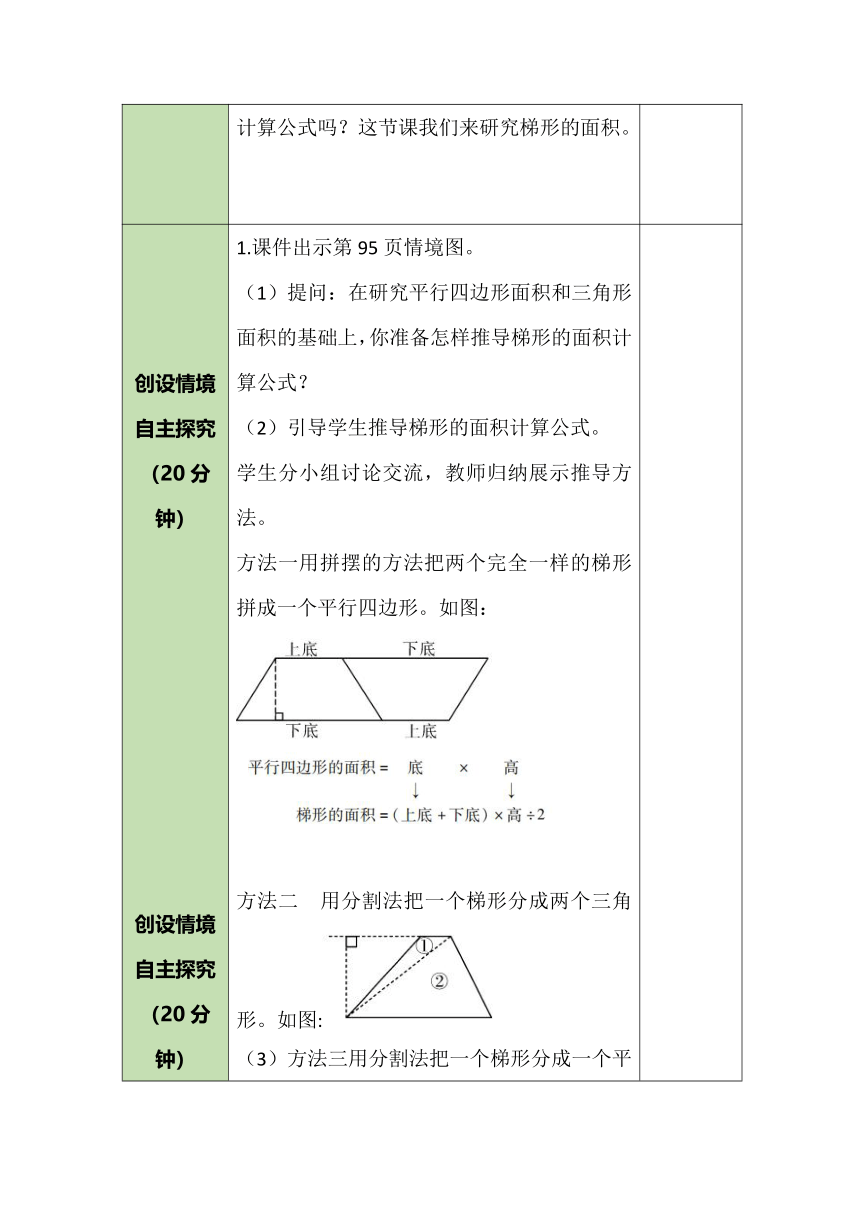
自主探究(20分钟) 1.课件出示第95页情境图。
(1)提问:在研究平行四边形面积和三角形面积的基础上,你准备怎样推导梯形的面积计算公式?
(2)引导学生推导梯形的面积计算公式。
学生分小组讨论交流,教师归纳展示推导方法。
方法一用拼摆的方法把两个完全一样的梯形拼成一个平行四边形。如图:
方法二 用分割法把一个梯形分成两个三角形。如图:
(3)方法三用分割法把一个梯形分成一个平行四边形和一个三角形。如图:
同理方法二、三都能推导出梯形的面积=(上底+下底)×高÷2。
(3)引导学生用字母表示梯形的面积公式。
如果用S表示梯形的面积,a表示梯形的上底,b表示梯形的下底,h表示梯形的高,你能用字母表示梯形的面积计算公式吗?
学生交流后回答,教师板书:
梯形的面积计算公式:S=(a+b)h÷2。
2.课件出示例3。
提问:你们能用所学的知识计算这个直角梯形的面积吗?
学生尝试计算,并交流汇报,教师板书:S=(a+b)h÷2=(36+120)×135÷2=156×135÷2=10530(m2)
课堂练习 巩固提高
(12分钟) 1.完成教材第96页“做一做”。
2.完成教材第97页“练习二十一”第1、2题。
3.完成教材第97页“练习二十一”第5题。
4.完成教材第98页“练习二十一”第6题。
课堂小结 课后作业
(3分钟) 1.(1)教师总结本节课的学习内容。
(2)学生谈本节课学习的收获。
2.布置作业。
见本书配套练习题。
课堂板书
教学反思 梯形的面积计算公式推导方法与三角形的面积计算公式推导方法有很大的相似之处,放手让学生自己利用前面的学习经验,推导出梯形的面积计算公式。尊重学生的认知规律,注重知识的前后联系。引导学生从不同的途经推导出梯形的面积计算公式。促进了学生的思维发展,培养学生的自学能力和探索精神。
教学目标 1.理解和掌握梯形的面积计算公式,能运用公式正确地计算梯形的面积,并能运用公式解决实际问题。
2.理解梯形面积计算公式的推导过程,培养学生的自我探索精神。
3.提高学生运用知识解决问题的能力,培养分析概括和思考的能力。
重点难点 重点:理解并掌握梯形的面积计算公式,能运用公式解决实际问题。
难点:理解梯形面积计算公式的推导过程。
教学内容 对应教材第95页内容,第96页例3、“做一做”和第97~98页“练习二十一”的第1、2、5、6题。
教学准备 教具准备:PPT课件
教学过程
教学环节 教案设计 二次备课
回顾旧知 引入新课
(5分钟) 1.回顾以前所学知识,完成下列填空。
(1)梯形有( )条边,它的对边( )。
(2)平行四边形的面积=( )×( )
三角形的面积=( )×( )÷( )
2.引出课题,明确本节课的学习内容。
我们身边有很多物品的形状是梯形,如小汽车的车窗,你能用学过的方法推导出梯形的面积计算公式吗?这节课我们来研究梯形的面积。
创设情境
自主探究(20分钟)
创设情境
自主探究(20分钟) 1.课件出示第95页情境图。
(1)提问:在研究平行四边形面积和三角形面积的基础上,你准备怎样推导梯形的面积计算公式?
(2)引导学生推导梯形的面积计算公式。
学生分小组讨论交流,教师归纳展示推导方法。
方法一用拼摆的方法把两个完全一样的梯形拼成一个平行四边形。如图:
方法二 用分割法把一个梯形分成两个三角形。如图:
(3)方法三用分割法把一个梯形分成一个平行四边形和一个三角形。如图:
同理方法二、三都能推导出梯形的面积=(上底+下底)×高÷2。
(3)引导学生用字母表示梯形的面积公式。
如果用S表示梯形的面积,a表示梯形的上底,b表示梯形的下底,h表示梯形的高,你能用字母表示梯形的面积计算公式吗?
学生交流后回答,教师板书:
梯形的面积计算公式:S=(a+b)h÷2。
2.课件出示例3。
提问:你们能用所学的知识计算这个直角梯形的面积吗?
学生尝试计算,并交流汇报,教师板书:S=(a+b)h÷2=(36+120)×135÷2=156×135÷2=10530(m2)
课堂练习 巩固提高
(12分钟) 1.完成教材第96页“做一做”。
2.完成教材第97页“练习二十一”第1、2题。
3.完成教材第97页“练习二十一”第5题。
4.完成教材第98页“练习二十一”第6题。
课堂小结 课后作业
(3分钟) 1.(1)教师总结本节课的学习内容。
(2)学生谈本节课学习的收获。
2.布置作业。
见本书配套练习题。
课堂板书
教学反思 梯形的面积计算公式推导方法与三角形的面积计算公式推导方法有很大的相似之处,放手让学生自己利用前面的学习经验,推导出梯形的面积计算公式。尊重学生的认知规律,注重知识的前后联系。引导学生从不同的途经推导出梯形的面积计算公式。促进了学生的思维发展,培养学生的自学能力和探索精神。
