2019-2020学年山东省聊城市阳谷县八年级下学期期末数学试卷 (word版,解析版)
文档属性
| 名称 | 2019-2020学年山东省聊城市阳谷县八年级下学期期末数学试卷 (word版,解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 06:24:00 | ||
图片预览




文档简介
2019-2020学年山东聊城市阳谷县八年级第二学期期末数学试卷
一、选择题(共12小题).
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列实数中,无理数的个数是( )
①0.333;②;③;④π;⑤6.18118111811118……
A.1个 B.2个 C.3个 D.4个
3.下列式子不正确的是( )
A.=4a2 B.?=5
C.== D.﹣=
4.在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2,则点A,点B表示的数分别是( )
A.﹣, B.,﹣ C.0,2 D.﹣2,2
5.已知y是x的一次函数,下表列出了部分y与x的对应值:
x ﹣1 0 1 2
y ﹣2 ﹣1 0 a
则a的值为( )
A.﹣2 B.1 C.2 D.3
6.若a>0,b<0,a+b>0,则a,b,﹣a,﹣b按照从小到大的顺序用“<”连接起来,正确的是( )
A.﹣a<b<﹣b<a B.a>﹣b>b>﹣a C.b<﹣a<﹣b<a D.﹣a<﹣b<b<a
7.实数a,b在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A.a﹣5>b﹣5 B.﹣a>﹣b C.6a>6b D.a﹣b>0
8.若=a,=b,则的值用a、b可以表示为( )
A. B. C. D.
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为( )
A.11 B.10 C.9 D.8
10.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
A.4 B. C.2 D.1
11.如图,已知正比例函数y1=kx与一次函数y2=﹣x+b的图象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<﹣2时,kx>﹣x+b.其中正确的是( )
A.①③ B.②③ C.③④ D.①④
12.有如下按规律排列的数表,将这些数计算出来,并按原数表中的顺序排列得到一串数列:1,,,,2,,,,3,5,……
那么5是这串数列中的第几个数.( )
A.10 B.13
C.10或13 D.第5行第3个数
二、填空题(本题共6小题,每小题4分,满分24分)
13.代数式在实数范围内有意义,则x的取值范围是 .
14.如图,在平面直角坐标系xOy中,直线l1:y=mx﹣2与直线l2:y=x+n相交于点P,则关于x,y的二元一次方程组的解是 .
15.如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是 .
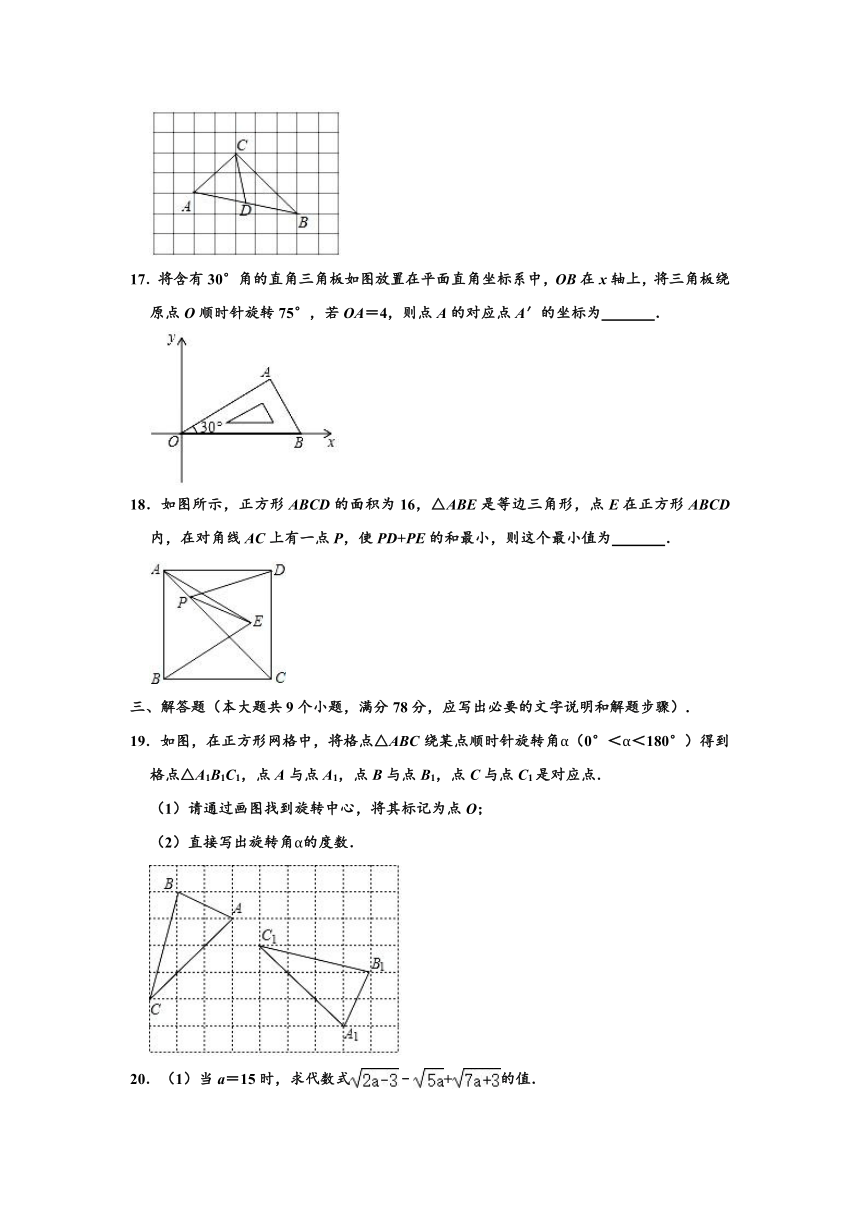
16.如图,每个小正方形的边长为1,在△ABC中,点A,B,C均在格点上,点D为AB的中点,则线段CD的长为 .
17.将含有30°角的直角三角板如图放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转75°,若OA=4,则点A的对应点A′的坐标为 .
18.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 .
三、解答题(本大题共9个小题,满分78分,应写出必要的文字说明和解题步骤).
19.如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画图找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
20.(1)当a=15时,求代数式﹣+的值.
(2)已知x﹣1=,求代数式(x+1)2﹣4(x+1)+4的值.
21.解不等式组:
(1).
(2),并写出这个不等式的所有整数解.
22.为保障疫情防控期间武汉蔬菜供应,2020年1月份山东寿光首批350吨蔬菜无偿捐给武汉,现有A、B两种型号的汽车调用.已知A型汽车每辆可装蔬菜20吨,B型汽车每辆可装15吨,在每辆汽车不超载的情况下,要把这350吨蔬菜一次性装运完,并且A型汽车确定要用8辆,问至少调用B型车多少辆?
23.如图,?ABCD中,E,F为对角线AC上的两点,且BE∥DF;求证:AE=CF.
24.如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
25.如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边落在对角线BD上,点A落在点A′处,折痕为DG,求AG的长.
26.现代互联网技术的厂泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>l时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
27.我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.
(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是 (请填序号);
(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.
①如图1,求证:AC平分∠BCD;
小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:
想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;
想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在一条直线上,从而可证AC平分∠BCD.
请你参考上面的想法,帮助小明证明AC平分∠BCD;
②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.
参考答案
一、选择题(共12小题).
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的概念对各选项分析判断后利用排除法求解.
解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误.
故选:B.
2.下列实数中,无理数的个数是( )
①0.333;②;③;④π;⑤6.18118111811118……
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,结合选项,找出无理数的个数即可.
解:根据无理数的三种形式可得,③,④π,⑤6.18118111811118…是无理数,共3个,
故选:C.
3.下列式子不正确的是( )
A.=4a2 B.?=5
C.== D.﹣=
【分析】利用二次根式的性质对A、C进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的加减法对D进行判断.
解:A、原式=4a2,所以A选项的计算正确;
B、原式==5,所以B选项的计算正确;
C、原式==(a>0),所以C选项的计算正确;
D、与﹣不能合并,所以D选项的计算不正确.
故选:D.
4.在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2,则点A,点B表示的数分别是( )
A.﹣, B.,﹣ C.0,2 D.﹣2,2
【分析】根据相反数的定义即可求解.
解:由A、B表示的数互为相反数,且AB=2,点A在点B的左边,得
点A、B表示的数是﹣,.
故选:A.
5.已知y是x的一次函数,下表列出了部分y与x的对应值:
x ﹣1 0 1 2
y ﹣2 ﹣1 0 a
则a的值为( )
A.﹣2 B.1 C.2 D.3
【分析】利用待定系数法即可求得函数的解析式,然后把x=2代入解析式即可求得a的值.
解:设一次函数的表达式为y=kx+b.
代入(1,0),(0,﹣1)两点,得:
∴.
解得:.
∴一次函数表达式为y=x﹣1.
把(2,a)代入y=x﹣1,解得a=1.
故选:B.
6.若a>0,b<0,a+b>0,则a,b,﹣a,﹣b按照从小到大的顺序用“<”连接起来,正确的是( )
A.﹣a<b<﹣b<a B.a>﹣b>b>﹣a C.b<﹣a<﹣b<a D.﹣a<﹣b<b<a
【分析】由题意可知|a|>|b|,再根据有理数的大小比较法则比较即可.
解:∵a>0,b<0,a+b>0,,
∴|a|>|b|,如图,
∴﹣a<b<﹣b<a.
故选:A.
7.实数a,b在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A.a﹣5>b﹣5 B.﹣a>﹣b C.6a>6b D.a﹣b>0
【分析】根据数轴判断出a、b的正负情况以及绝对值的大小,然后解答即可.
解:由图可知,b<0<a,且|b|<|a|,
∴a﹣5>b﹣5,﹣a<﹣b,6a>6b,a﹣b>0,
∴关系式不成立的是选项B.
故选:B.
8.若=a,=b,则的值用a、b可以表示为( )
A. B. C. D.
【分析】,化简即可.
解:=.
故选:C.
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为( )
A.11 B.10 C.9 D.8
【分析】利用平行四边形的性质可知AO=3,在Rt△ABO中利用勾股定理可得BO=5,则BD=2BO=10.
解:∵四边形ABCD是平行四边形,
∴BD=2BO,AO=OC=3.
在Rt△ABO中,利用勾股定理可得BO==5.
∴BD=2BO=10.
故选:B.
10.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
A.4 B. C.2 D.1
【分析】连接AC,根据正方形ABCD的面积为8,求得AC=4,根据菱形的面积,即可得到结论.
解:连接AC,
∵正方形ABCD的面积为8,
∴AC=4,
∵菱形AECF的面积为4,
∴EF==2,
故选:C.
11.如图,已知正比例函数y1=kx与一次函数y2=﹣x+b的图象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<﹣2时,kx>﹣x+b.其中正确的是( )
A.①③ B.②③ C.③④ D.①④
【分析】根据正比例函数和一次函数的性质判断即可.
解:∵直线y1=kx经过第一、三象限,
∴k>0,故①正确;
∵y2=﹣x+b与y轴交点在负半轴,
∴b<0,故②错误;
∵正比例函数y1=kx经过原点,且y随x的增大而增大,
∴当x>0时,y1>0;故③正确;
当x<﹣2时,正比例函数y1=kx在一次函数y2=﹣x+b图象的下方,即kx<﹣x+b,故④错误.
故选:A.
12.有如下按规律排列的数表,将这些数计算出来,并按原数表中的顺序排列得到一串数列:1,,,,2,,,,3,5,……
那么5是这串数列中的第几个数.( )
A.10 B.13
C.10或13 D.第5行第3个数
【分析】观察阅读材料中的规律,确定出所求即可.
解:5═,则5是第4行第4个数或第5行第3个数,
即5是这串数列中的第10或13个数.
故选:C.
二、填空题(本题共6小题,每小题4分,满分24分)
13.代数式在实数范围内有意义,则x的取值范围是 x≥1 .
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
解:∵在实数范围内有意义,
∴x﹣1≥0,
解得x≥1.
故答案为:x≥1.
14.如图,在平面直角坐标系xOy中,直线l1:y=mx﹣2与直线l2:y=x+n相交于点P,则关于x,y的二元一次方程组的解是 .
【分析】关于x、y的二元一次方程组的解即为直线l1:y=mx﹣2与直线l2:y=x+n的交点P(1,2)的坐标.
解:∵直线l1:y=mx﹣2与直线l2:y=x+n相交于点P(1,2),
∴关于x、y的二元一次方程组的解是.
故答案为.
15.如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是 16 .
【分析】根据题意,OM垂直平分AC,所以MC=MA,因此△CDM的周长=AD+CD,可得平行四边形ABCD的周长.
解:∵ABCD是平行四边形,
∴OA=OC,
∵OM⊥AC,
∴AM=MC.
∴△CDM的周长=AD+CD=8,
∴平行四边形ABCD的周长是2×8=16.
故答案为16.
16.如图,每个小正方形的边长为1,在△ABC中,点A,B,C均在格点上,点D为AB的中点,则线段CD的长为 .
【分析】利用勾股定理的逆定理证明∠ACB=90°,再利用直角三角形斜边中线的性质即可解决问题.
解:∵AC=2,BC=3,AB=,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵AD=DB,
∴CD=AB=,
故答案为.
17.将含有30°角的直角三角板如图放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转75°,若OA=4,则点A的对应点A′的坐标为 (,) .
【分析】根据旋转的性质将三角板绕原点O顺时针旋转75°,OA=4,再根据等腰直角三角形的性质即可求点A的对应点A′的坐标.
解:如图,
将三角板绕原点O顺时针旋转75°得△A′OB′,
∴OA′=OA=4,
∵∠AOB=30°,
∴∠BOA′=75°﹣30°=45°,
作A′C⊥OB于点C,
∴∠A′CO=90°,
∴∠OA′C=45°,
∴OC=A′C=OA′?=2.
所以点A的对应点A′的坐标为(2,﹣2).
故答案为:(2,﹣2).
18.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 4 .
【分析】先求得正方形的边长,依据等边三角形的定义可知BE=AB=4,连结BP,依据正方形的对称性可知PB=PD,则PE+PD=PE+BP.由两点之间线段最短可知:当点B、P、E在一条直线上时,PE+PD有最小值,最小值为BE的长.
解:连结BP.
∵四边形ABCD为正方形,面积为16,
∴正方形的边长为4.
∵△ABE为等边三角形,
∴BE=AB=4.
∵四边形ABCD为正方形,
∴△ABP与△ADP关于AC对称.
∴BP=DP.
∴PE+PD=PE+BP.
由两点之间线段最短可知:当点B、P、E在一条直线上时,PE+PD有最小值,最小值=BE=4.
故答案为:4.
三、解答题(本大题共9个小题,满分78分,应写出必要的文字说明和解题步骤).
19.如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画图找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
【分析】(1)连接CC1、AA1,再分别作两线段的中垂线,两中垂线的交点即为所求;
(2)连接CO、C1O,结合网格特点可得旋转角∠COC1=α=90°.
解:(1)如图所示,点O即为所求;
(2)如图所示,∠COC1=α=90°.
20.(1)当a=15时,求代数式﹣+的值.
(2)已知x﹣1=,求代数式(x+1)2﹣4(x+1)+4的值.
【分析】(1)直接把a的值代入化简得出答案;
(2)直接利用完全平方公式将原式变形进而把已知代入得出答案.
解:(1)当a=15时,原式=﹣+
=3﹣5+6
=4;
(2)(x+1)2﹣4(x+1)+4
=(x+1﹣2)2
=(x﹣1)2,
∵x﹣1=,
∴原式=()2
=3.
21.解不等式组:
(1).
(2),并写出这个不等式的所有整数解.
【分析】(1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出所有整数解.
解:(1)解不等式3(x﹣2)<2x﹣2,得:x<4,
解不等式<x,得:x>,
则不等式组的解集为<x<4;
(2)解不等式5x﹣1≤3(x+1),得:x≤2,
解不等式﹣2x<1,得:x>﹣,
则不等式组的解集为﹣<x≤2,
所以不等式组的整数解为0、1、2.
22.为保障疫情防控期间武汉蔬菜供应,2020年1月份山东寿光首批350吨蔬菜无偿捐给武汉,现有A、B两种型号的汽车调用.已知A型汽车每辆可装蔬菜20吨,B型汽车每辆可装15吨,在每辆汽车不超载的情况下,要把这350吨蔬菜一次性装运完,并且A型汽车确定要用8辆,问至少调用B型车多少辆?
【分析】设调用B型汽车x辆,根据8辆A汽车的装货物的吨数+B汽车装货物的吨数≥350吨,由此列出不等式,求出x的值即可得出答案.
解:设调用B型汽车x辆,
由题意,得20×8+15x≥350.
解得x≥12.6.
又∵x是正整数,
∴x最小值=13.
答:至少调用B型车13辆.
23.如图,?ABCD中,E,F为对角线AC上的两点,且BE∥DF;求证:AE=CF.
【分析】根据已知条件利用AAS来判定△ADF≌△CBE,从而得出AE=CF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB.
∴∠BCE=∠DAF.
∵BE∥DF,
∴∠AFD=∠CEB
在△CDF和△ABE中,,
∴△CDF≌△ABE(AAS),
∴CE=AF,
∴AE=CF.
24.如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
【分析】(1)利用矩形的性质,得出点D坐标,进一步利用待定系数法求得函数解析式;
(2)由三角形的面积公式解答.
解:(1)由矩形ABCD的边AD=3,A(,0),B(2,0),
可得D(,3),C(2,3).
把B(2,0),D(,3)代入y=kx+b(k≠0)得,
.
解得:.
∴直线表达式为:y=﹣2x+4.
(2)连接CM.
∵B(2,0),
∴OB=2.
∴S△BCM=?BC?OB=×3×2=3.
25.如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边落在对角线BD上,点A落在点A′处,折痕为DG,求AG的长.
【分析】折叠的性质得∠BA′G=∠DA′G=∠A=90°,A′D=AD=6,由勾股定理得BD==10,得出A′B=4,设AG=A′G=x,则GB=8﹣x,由勾股定理得出方程,解方程即可得出结果.
解:∵矩形ABCD折叠后AD边落在BD上,
∴∠BA′G=∠DA′G=∠A=90°,
∵AB=8,AD=6,
∴A′D=6,BD===10,
∴A′B=4,
设AG=A′G=x,则GB=8﹣x,
由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴AG=3.
26.现代互联网技术的厂泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>l时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
【分析】(1)根据题意可以得到甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)根据题意和(1)中的函数解析式,可以列出相应的不等式,从而可以解答本题.
解:(1)由题意可得,
y甲=22+15(x﹣1)=15x+7,
y乙=16x+3;
(2)x>1时,令y甲<y乙,
即15x+7<16x+3
解得:x>4,
令y甲=y乙,
即15x+7=16x+3,
解得:x=4,
令y甲>y乙,
即15x+7>16x+3,
解得:x<4,
综上可知:当1<x<4时,选乙快递公司省钱;当x=4时,选甲、乙两家快递公司快递费一样多;当x>4时,选甲快递公司省钱.
27.我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.
(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是 ④ (请填序号);
(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.
①如图1,求证:AC平分∠BCD;
小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:
想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;
想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在一条直线上,从而可证AC平分∠BCD.
请你参考上面的想法,帮助小明证明AC平分∠BCD;
②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.
【分析】(1)由“完美四边形”定义可求解;
(2)①想法一:由“SAS”可证△ADC≌△ABE,可得∠ACD=∠AEB,AC=AE,由等腰三角形的性质可得结论;
想法二:由旋转的性质可得∠ADC=∠ABE,∠ACD=∠AEB,AC=AE,可证点C,B,E在一条直线上,由等腰三角形的性质可得结论;
②延长CB使BE=CD,连接AE,由①可得△ACE为等腰三角形,由∠BAD=90°,可证△ACE为等腰直角三角形,即可得解.
解:(1)由“完美四边形”的定义可得正方形是“完美四边形”.
故答案为:④
(2)
①想法一:延长CB使BE=CD,连接AE
∵∠ADC+∠ABC=180°,∠ABE+∠ABC=180°,
∴∠ADC=∠ABE
∵AD=AB,
∴△ADC≌△ABE(SAS)
∴∠ACD=∠AEB,AC=AE
∴∠ACB=∠AEB.
∴∠ACD=∠ACB.
即AC平分∠BCD4
想法二:将△ACD绕点A顺时针旋转,使AD边与AB边重合,得到△ABE,
∴△ADC≌△ABE.
∴∠ADC=∠ABE;
∠ACD=∠AEB;
AC=AE.
∵∠ADC+∠ABC=180°,
∴∠ABE+∠ABC=180°.
∴点C,B,E在一条直线上.
∵AC=AE,
∴∠ACB=∠AEB
∴∠ACD=∠ACB
即AC平分∠BCD
②BC+CD=AC
理由如下:
延长CB使BE=CD,连接AE,
由 ①得△ACE为等腰三角形.
∵∠BAD=90°,
∴∠EAC=90°
∴CE2=2AC2,
∴.
∴BC+CD=AC.
一、选择题(共12小题).
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
2.下列实数中,无理数的个数是( )
①0.333;②;③;④π;⑤6.18118111811118……
A.1个 B.2个 C.3个 D.4个
3.下列式子不正确的是( )
A.=4a2 B.?=5
C.== D.﹣=
4.在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2,则点A,点B表示的数分别是( )
A.﹣, B.,﹣ C.0,2 D.﹣2,2
5.已知y是x的一次函数,下表列出了部分y与x的对应值:
x ﹣1 0 1 2
y ﹣2 ﹣1 0 a
则a的值为( )
A.﹣2 B.1 C.2 D.3
6.若a>0,b<0,a+b>0,则a,b,﹣a,﹣b按照从小到大的顺序用“<”连接起来,正确的是( )
A.﹣a<b<﹣b<a B.a>﹣b>b>﹣a C.b<﹣a<﹣b<a D.﹣a<﹣b<b<a
7.实数a,b在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A.a﹣5>b﹣5 B.﹣a>﹣b C.6a>6b D.a﹣b>0
8.若=a,=b,则的值用a、b可以表示为( )
A. B. C. D.
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为( )
A.11 B.10 C.9 D.8
10.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
A.4 B. C.2 D.1
11.如图,已知正比例函数y1=kx与一次函数y2=﹣x+b的图象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<﹣2时,kx>﹣x+b.其中正确的是( )
A.①③ B.②③ C.③④ D.①④
12.有如下按规律排列的数表,将这些数计算出来,并按原数表中的顺序排列得到一串数列:1,,,,2,,,,3,5,……
那么5是这串数列中的第几个数.( )
A.10 B.13
C.10或13 D.第5行第3个数
二、填空题(本题共6小题,每小题4分,满分24分)
13.代数式在实数范围内有意义,则x的取值范围是 .
14.如图,在平面直角坐标系xOy中,直线l1:y=mx﹣2与直线l2:y=x+n相交于点P,则关于x,y的二元一次方程组的解是 .
15.如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是 .
16.如图,每个小正方形的边长为1,在△ABC中,点A,B,C均在格点上,点D为AB的中点,则线段CD的长为 .
17.将含有30°角的直角三角板如图放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转75°,若OA=4,则点A的对应点A′的坐标为 .
18.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 .
三、解答题(本大题共9个小题,满分78分,应写出必要的文字说明和解题步骤).
19.如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画图找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
20.(1)当a=15时,求代数式﹣+的值.
(2)已知x﹣1=,求代数式(x+1)2﹣4(x+1)+4的值.
21.解不等式组:
(1).
(2),并写出这个不等式的所有整数解.
22.为保障疫情防控期间武汉蔬菜供应,2020年1月份山东寿光首批350吨蔬菜无偿捐给武汉,现有A、B两种型号的汽车调用.已知A型汽车每辆可装蔬菜20吨,B型汽车每辆可装15吨,在每辆汽车不超载的情况下,要把这350吨蔬菜一次性装运完,并且A型汽车确定要用8辆,问至少调用B型车多少辆?
23.如图,?ABCD中,E,F为对角线AC上的两点,且BE∥DF;求证:AE=CF.
24.如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
25.如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边落在对角线BD上,点A落在点A′处,折痕为DG,求AG的长.
26.现代互联网技术的厂泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>l时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
27.我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.
(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是 (请填序号);
(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.
①如图1,求证:AC平分∠BCD;
小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:
想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;
想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在一条直线上,从而可证AC平分∠BCD.
请你参考上面的想法,帮助小明证明AC平分∠BCD;
②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.
参考答案
一、选择题(共12小题).
1.随着国民经济快速发展,我国涌现出一批规模大、效益高的企业,如大疆、国家核电、华为、凤凰光学等,以上四个企业的标志是中心对称图形的是( )
A. B.
C. D.
【分析】根据中心对称图形的概念对各选项分析判断后利用排除法求解.
解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误.
故选:B.
2.下列实数中,无理数的个数是( )
①0.333;②;③;④π;⑤6.18118111811118……
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,结合选项,找出无理数的个数即可.
解:根据无理数的三种形式可得,③,④π,⑤6.18118111811118…是无理数,共3个,
故选:C.
3.下列式子不正确的是( )
A.=4a2 B.?=5
C.== D.﹣=
【分析】利用二次根式的性质对A、C进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的加减法对D进行判断.
解:A、原式=4a2,所以A选项的计算正确;
B、原式==5,所以B选项的计算正确;
C、原式==(a>0),所以C选项的计算正确;
D、与﹣不能合并,所以D选项的计算不正确.
故选:D.
4.在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2,则点A,点B表示的数分别是( )
A.﹣, B.,﹣ C.0,2 D.﹣2,2
【分析】根据相反数的定义即可求解.
解:由A、B表示的数互为相反数,且AB=2,点A在点B的左边,得
点A、B表示的数是﹣,.
故选:A.
5.已知y是x的一次函数,下表列出了部分y与x的对应值:
x ﹣1 0 1 2
y ﹣2 ﹣1 0 a
则a的值为( )
A.﹣2 B.1 C.2 D.3
【分析】利用待定系数法即可求得函数的解析式,然后把x=2代入解析式即可求得a的值.
解:设一次函数的表达式为y=kx+b.
代入(1,0),(0,﹣1)两点,得:
∴.
解得:.
∴一次函数表达式为y=x﹣1.
把(2,a)代入y=x﹣1,解得a=1.
故选:B.
6.若a>0,b<0,a+b>0,则a,b,﹣a,﹣b按照从小到大的顺序用“<”连接起来,正确的是( )
A.﹣a<b<﹣b<a B.a>﹣b>b>﹣a C.b<﹣a<﹣b<a D.﹣a<﹣b<b<a
【分析】由题意可知|a|>|b|,再根据有理数的大小比较法则比较即可.
解:∵a>0,b<0,a+b>0,,
∴|a|>|b|,如图,
∴﹣a<b<﹣b<a.
故选:A.
7.实数a,b在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A.a﹣5>b﹣5 B.﹣a>﹣b C.6a>6b D.a﹣b>0
【分析】根据数轴判断出a、b的正负情况以及绝对值的大小,然后解答即可.
解:由图可知,b<0<a,且|b|<|a|,
∴a﹣5>b﹣5,﹣a<﹣b,6a>6b,a﹣b>0,
∴关系式不成立的是选项B.
故选:B.
8.若=a,=b,则的值用a、b可以表示为( )
A. B. C. D.
【分析】,化简即可.
解:=.
故选:C.
9.如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长为( )
A.11 B.10 C.9 D.8
【分析】利用平行四边形的性质可知AO=3,在Rt△ABO中利用勾股定理可得BO=5,则BD=2BO=10.
解:∵四边形ABCD是平行四边形,
∴BD=2BO,AO=OC=3.
在Rt△ABO中,利用勾股定理可得BO==5.
∴BD=2BO=10.
故选:B.
10.如图,正方形ABCD的面积为8,菱形AECF的面积为4,则EF的长是( )
A.4 B. C.2 D.1
【分析】连接AC,根据正方形ABCD的面积为8,求得AC=4,根据菱形的面积,即可得到结论.
解:连接AC,
∵正方形ABCD的面积为8,
∴AC=4,
∵菱形AECF的面积为4,
∴EF==2,
故选:C.
11.如图,已知正比例函数y1=kx与一次函数y2=﹣x+b的图象交于点P.下面有四个结论:
①k>0;②b>0;③当x>0时,y1>0;④当x<﹣2时,kx>﹣x+b.其中正确的是( )
A.①③ B.②③ C.③④ D.①④
【分析】根据正比例函数和一次函数的性质判断即可.
解:∵直线y1=kx经过第一、三象限,
∴k>0,故①正确;
∵y2=﹣x+b与y轴交点在负半轴,
∴b<0,故②错误;
∵正比例函数y1=kx经过原点,且y随x的增大而增大,
∴当x>0时,y1>0;故③正确;
当x<﹣2时,正比例函数y1=kx在一次函数y2=﹣x+b图象的下方,即kx<﹣x+b,故④错误.
故选:A.
12.有如下按规律排列的数表,将这些数计算出来,并按原数表中的顺序排列得到一串数列:1,,,,2,,,,3,5,……
那么5是这串数列中的第几个数.( )
A.10 B.13
C.10或13 D.第5行第3个数
【分析】观察阅读材料中的规律,确定出所求即可.
解:5═,则5是第4行第4个数或第5行第3个数,
即5是这串数列中的第10或13个数.
故选:C.
二、填空题(本题共6小题,每小题4分,满分24分)
13.代数式在实数范围内有意义,则x的取值范围是 x≥1 .
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
解:∵在实数范围内有意义,
∴x﹣1≥0,
解得x≥1.
故答案为:x≥1.
14.如图,在平面直角坐标系xOy中,直线l1:y=mx﹣2与直线l2:y=x+n相交于点P,则关于x,y的二元一次方程组的解是 .
【分析】关于x、y的二元一次方程组的解即为直线l1:y=mx﹣2与直线l2:y=x+n的交点P(1,2)的坐标.
解:∵直线l1:y=mx﹣2与直线l2:y=x+n相交于点P(1,2),
∴关于x、y的二元一次方程组的解是.
故答案为.
15.如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么?ABCD的周长是 16 .
【分析】根据题意,OM垂直平分AC,所以MC=MA,因此△CDM的周长=AD+CD,可得平行四边形ABCD的周长.
解:∵ABCD是平行四边形,
∴OA=OC,
∵OM⊥AC,
∴AM=MC.
∴△CDM的周长=AD+CD=8,
∴平行四边形ABCD的周长是2×8=16.
故答案为16.
16.如图,每个小正方形的边长为1,在△ABC中,点A,B,C均在格点上,点D为AB的中点,则线段CD的长为 .
【分析】利用勾股定理的逆定理证明∠ACB=90°,再利用直角三角形斜边中线的性质即可解决问题.
解:∵AC=2,BC=3,AB=,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∵AD=DB,
∴CD=AB=,
故答案为.
17.将含有30°角的直角三角板如图放置在平面直角坐标系中,OB在x轴上,将三角板绕原点O顺时针旋转75°,若OA=4,则点A的对应点A′的坐标为 (,) .
【分析】根据旋转的性质将三角板绕原点O顺时针旋转75°,OA=4,再根据等腰直角三角形的性质即可求点A的对应点A′的坐标.
解:如图,
将三角板绕原点O顺时针旋转75°得△A′OB′,
∴OA′=OA=4,
∵∠AOB=30°,
∴∠BOA′=75°﹣30°=45°,
作A′C⊥OB于点C,
∴∠A′CO=90°,
∴∠OA′C=45°,
∴OC=A′C=OA′?=2.
所以点A的对应点A′的坐标为(2,﹣2).
故答案为:(2,﹣2).
18.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为 4 .
【分析】先求得正方形的边长,依据等边三角形的定义可知BE=AB=4,连结BP,依据正方形的对称性可知PB=PD,则PE+PD=PE+BP.由两点之间线段最短可知:当点B、P、E在一条直线上时,PE+PD有最小值,最小值为BE的长.
解:连结BP.
∵四边形ABCD为正方形,面积为16,
∴正方形的边长为4.
∵△ABE为等边三角形,
∴BE=AB=4.
∵四边形ABCD为正方形,
∴△ABP与△ADP关于AC对称.
∴BP=DP.
∴PE+PD=PE+BP.
由两点之间线段最短可知:当点B、P、E在一条直线上时,PE+PD有最小值,最小值=BE=4.
故答案为:4.
三、解答题(本大题共9个小题,满分78分,应写出必要的文字说明和解题步骤).
19.如图,在正方形网格中,将格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点.
(1)请通过画图找到旋转中心,将其标记为点O;
(2)直接写出旋转角α的度数.
【分析】(1)连接CC1、AA1,再分别作两线段的中垂线,两中垂线的交点即为所求;
(2)连接CO、C1O,结合网格特点可得旋转角∠COC1=α=90°.
解:(1)如图所示,点O即为所求;
(2)如图所示,∠COC1=α=90°.
20.(1)当a=15时,求代数式﹣+的值.
(2)已知x﹣1=,求代数式(x+1)2﹣4(x+1)+4的值.
【分析】(1)直接把a的值代入化简得出答案;
(2)直接利用完全平方公式将原式变形进而把已知代入得出答案.
解:(1)当a=15时,原式=﹣+
=3﹣5+6
=4;
(2)(x+1)2﹣4(x+1)+4
=(x+1﹣2)2
=(x﹣1)2,
∵x﹣1=,
∴原式=()2
=3.
21.解不等式组:
(1).
(2),并写出这个不等式的所有整数解.
【分析】(1)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,从而得出所有整数解.
解:(1)解不等式3(x﹣2)<2x﹣2,得:x<4,
解不等式<x,得:x>,
则不等式组的解集为<x<4;
(2)解不等式5x﹣1≤3(x+1),得:x≤2,
解不等式﹣2x<1,得:x>﹣,
则不等式组的解集为﹣<x≤2,
所以不等式组的整数解为0、1、2.
22.为保障疫情防控期间武汉蔬菜供应,2020年1月份山东寿光首批350吨蔬菜无偿捐给武汉,现有A、B两种型号的汽车调用.已知A型汽车每辆可装蔬菜20吨,B型汽车每辆可装15吨,在每辆汽车不超载的情况下,要把这350吨蔬菜一次性装运完,并且A型汽车确定要用8辆,问至少调用B型车多少辆?
【分析】设调用B型汽车x辆,根据8辆A汽车的装货物的吨数+B汽车装货物的吨数≥350吨,由此列出不等式,求出x的值即可得出答案.
解:设调用B型汽车x辆,
由题意,得20×8+15x≥350.
解得x≥12.6.
又∵x是正整数,
∴x最小值=13.
答:至少调用B型车13辆.
23.如图,?ABCD中,E,F为对角线AC上的两点,且BE∥DF;求证:AE=CF.
【分析】根据已知条件利用AAS来判定△ADF≌△CBE,从而得出AE=CF.
【解答】证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB.
∴∠BCE=∠DAF.
∵BE∥DF,
∴∠AFD=∠CEB
在△CDF和△ABE中,,
∴△CDF≌△ABE(AAS),
∴CE=AF,
∴AE=CF.
24.如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(,0),B(2,0),直线y=kx+b(k≠0)经过B,D两点.
(1)求直线y=kx+b(k≠0)的表达式;
(2)若直线y=kx+b(k≠0)与y轴交于点M,求△CBM的面积.
【分析】(1)利用矩形的性质,得出点D坐标,进一步利用待定系数法求得函数解析式;
(2)由三角形的面积公式解答.
解:(1)由矩形ABCD的边AD=3,A(,0),B(2,0),
可得D(,3),C(2,3).
把B(2,0),D(,3)代入y=kx+b(k≠0)得,
.
解得:.
∴直线表达式为:y=﹣2x+4.
(2)连接CM.
∵B(2,0),
∴OB=2.
∴S△BCM=?BC?OB=×3×2=3.
25.如图,矩形纸片ABCD中,AB=8,AD=6,折叠纸片使AD边落在对角线BD上,点A落在点A′处,折痕为DG,求AG的长.
【分析】折叠的性质得∠BA′G=∠DA′G=∠A=90°,A′D=AD=6,由勾股定理得BD==10,得出A′B=4,设AG=A′G=x,则GB=8﹣x,由勾股定理得出方程,解方程即可得出结果.
解:∵矩形ABCD折叠后AD边落在BD上,
∴∠BA′G=∠DA′G=∠A=90°,
∵AB=8,AD=6,
∴A′D=6,BD===10,
∴A′B=4,
设AG=A′G=x,则GB=8﹣x,
由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴AG=3.
26.现代互联网技术的厂泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解甲、乙两家快递公司比较合适,甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费,乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)当x>l时,请分別直接写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)在(1)的条件下,小明选择哪家快递公司更省钱?
【分析】(1)根据题意可以得到甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)根据题意和(1)中的函数解析式,可以列出相应的不等式,从而可以解答本题.
解:(1)由题意可得,
y甲=22+15(x﹣1)=15x+7,
y乙=16x+3;
(2)x>1时,令y甲<y乙,
即15x+7<16x+3
解得:x>4,
令y甲=y乙,
即15x+7=16x+3,
解得:x=4,
令y甲>y乙,
即15x+7>16x+3,
解得:x<4,
综上可知:当1<x<4时,选乙快递公司省钱;当x=4时,选甲、乙两家快递公司快递费一样多;当x>4时,选甲快递公司省钱.
27.我们规定:一组邻边相等且对角互补的四边形叫作“完美四边形”.
(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是 ④ (请填序号);
(2)在“完美”四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.
①如图1,求证:AC平分∠BCD;
小明通过观察、实验,提出以下两种想法,证明AC平分∠BCD:
想法一:通过∠B+∠D=180°,可延长CB到E,使BE=CD,通过证明△AEB≌△ACD,从而可证AC平分∠BCD;
想法二:通过AB=AD,可将△ACD绕点A顺时针旋转,使AD与AB重合,得到△AEB,可证C,B,E三点在一条直线上,从而可证AC平分∠BCD.
请你参考上面的想法,帮助小明证明AC平分∠BCD;
②如图2,当∠BAD=90°,用等式表示线段AC,BC,CD之间的数量关系,并证明.
【分析】(1)由“完美四边形”定义可求解;
(2)①想法一:由“SAS”可证△ADC≌△ABE,可得∠ACD=∠AEB,AC=AE,由等腰三角形的性质可得结论;
想法二:由旋转的性质可得∠ADC=∠ABE,∠ACD=∠AEB,AC=AE,可证点C,B,E在一条直线上,由等腰三角形的性质可得结论;
②延长CB使BE=CD,连接AE,由①可得△ACE为等腰三角形,由∠BAD=90°,可证△ACE为等腰直角三角形,即可得解.
解:(1)由“完美四边形”的定义可得正方形是“完美四边形”.
故答案为:④
(2)
①想法一:延长CB使BE=CD,连接AE
∵∠ADC+∠ABC=180°,∠ABE+∠ABC=180°,
∴∠ADC=∠ABE
∵AD=AB,
∴△ADC≌△ABE(SAS)
∴∠ACD=∠AEB,AC=AE
∴∠ACB=∠AEB.
∴∠ACD=∠ACB.
即AC平分∠BCD4
想法二:将△ACD绕点A顺时针旋转,使AD边与AB边重合,得到△ABE,
∴△ADC≌△ABE.
∴∠ADC=∠ABE;
∠ACD=∠AEB;
AC=AE.
∵∠ADC+∠ABC=180°,
∴∠ABE+∠ABC=180°.
∴点C,B,E在一条直线上.
∵AC=AE,
∴∠ACB=∠AEB
∴∠ACD=∠ACB
即AC平分∠BCD
②BC+CD=AC
理由如下:
延长CB使BE=CD,连接AE,
由 ①得△ACE为等腰三角形.
∵∠BAD=90°,
∴∠EAC=90°
∴CE2=2AC2,
∴.
∴BC+CD=AC.
同课章节目录
