2019-2020学年湖南省衡阳市八年级下学期期末数学试卷 (word版,解析版)
文档属性
| 名称 | 2019-2020学年湖南省衡阳市八年级下学期期末数学试卷 (word版,解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 809.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 06:18:37 | ||
图片预览



文档简介
2019-2020学年湖南省衡阳市八年级第二学期期末数学试卷
一、选择题(共12小题).
1.分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x=2 D.x=﹣2
2.在平面直角坐标系中,点(﹣3,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若方程=2+有增根,则a的值为( )
A.a=﹣4 B.a=4 C.a=3 D.a=2
4.直线y=2x﹣1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
6.化简÷的结果是( )
A.x+3 B.x﹣3 C.3﹣x D.﹣6x
7.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
8.有一组数据:1,3,3,4,5,这组数据的众数为( )
A.1 B.3 C.4 D.5
9.如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
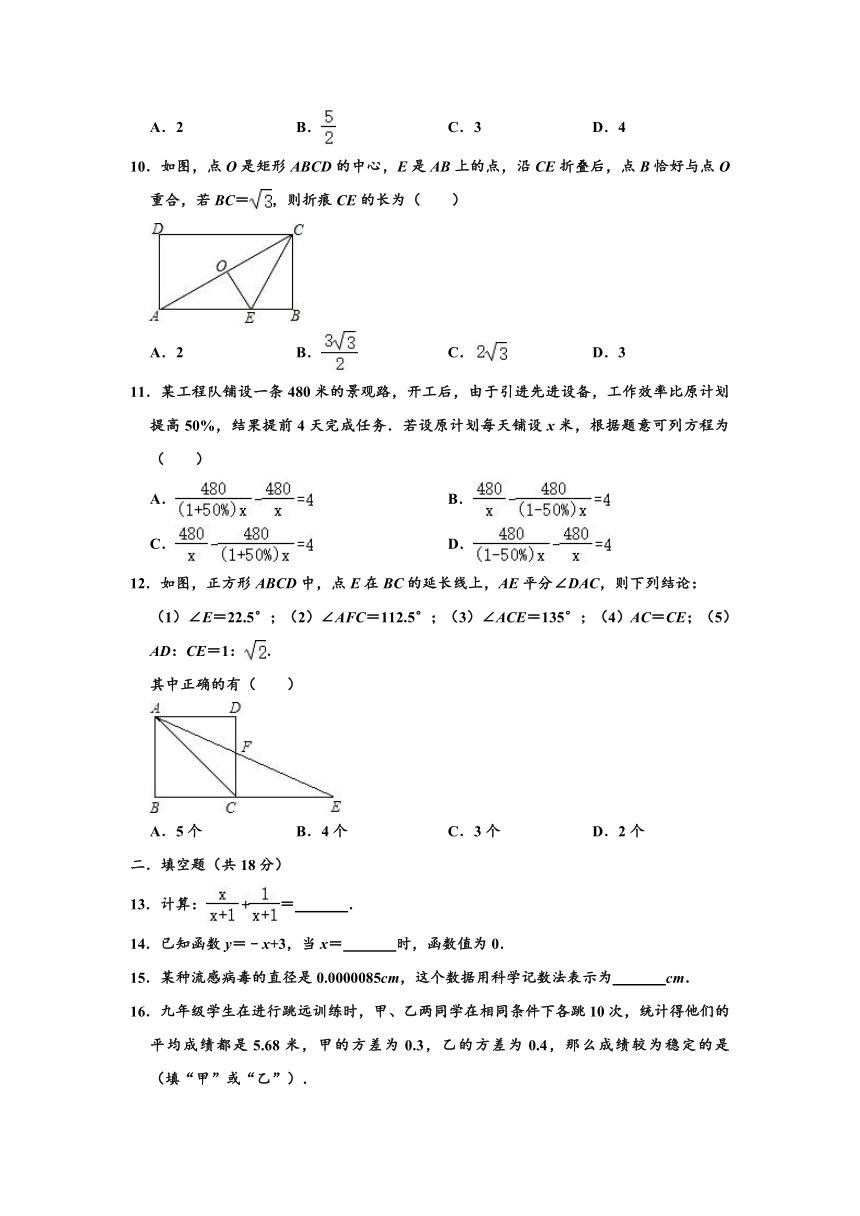
10.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=,则折痕CE的长为( )
A.2 B. C. D.3
11.某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )
A. B.
C. D.
12.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:
(1)∠E=22.5°;(2)∠AFC=112.5°;(3)∠ACE=135°;(4)AC=CE;(5)AD:CE=1:.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共18分)
13.计算:= .
14.已知函数y=﹣x+3,当x= 时,函数值为0.
15.某种流感病毒的直径是0.0000085cm,这个数据用科学记数法表示为 cm.
16.九年级学生在进行跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得他们的平均成绩都是5.68米,甲的方差为0.3,乙的方差为0.4,那么成绩较为稳定的是 (填“甲”或“乙”).
17.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
18.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k= .
三、解答题(共66分)
19.计算:(π﹣2016)0+()﹣1﹣×|﹣3|
20.解分式方程:+=2.
21.先化简:÷(﹣),再从﹣2<x<3的范围内选取一个你喜欢的x值代入求值.
22.如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
23. 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
每户丢弃废旧塑料袋(个) 频数(户) 频率
3 5 0.1
4 20 0.4
5
6 10 0.2
合计 50 1
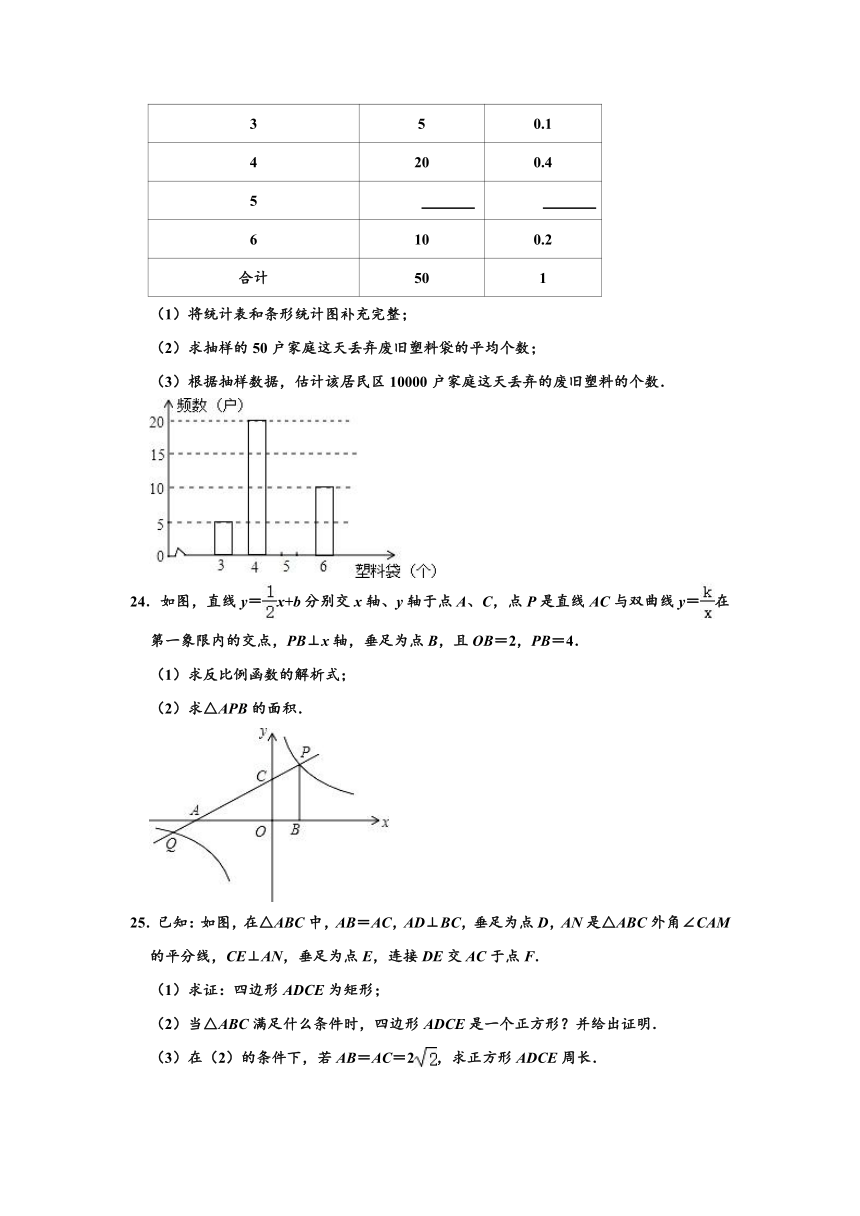
(1)将统计表和条形统计图补充完整;
(2)求抽样的50户家庭这天丢弃废旧塑料袋的平均个数;
(3)根据抽样数据,估计该居民区10000户家庭这天丢弃的废旧塑料的个数.
24.如图,直线y=x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积.
25.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
26.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求点D的坐标;
(2)问直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请写出点M的坐标.
参考答案
一、选择题(共12小题).
1.分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x=2 D.x=﹣2
解:根据题意得:x﹣2≠0,
解得:x≠2.
故选:A.
2.在平面直角坐标系中,点(﹣3,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点(﹣3,2)所在的象限在第二象限.
故选:B.
3.若方程=2+有增根,则a的值为( )
A.a=﹣4 B.a=4 C.a=3 D.a=2
【分析】分式方程去分母转化为整式方程,由分式方程有增根得到x﹣4=0,求出x的值,代入整式方程计算即可求出a的值.
解:去分母得:x=2(x﹣4)+a,
由分式方程有增根,得到x﹣4=0,即x=4,
把x=4代入整式方程得:a=4.
故选:B.
4.直线y=2x﹣1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据题目中的函数解析式和一次函数的性质可以解答本题.
解:∵y=2x﹣1,k=2>0,b=﹣1,
∴该函数经过第一、三、四象限,不经过第二象限,
故选:B.
5.若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
【分析】根据反比例函数图象上点的坐标特征,把三个点的坐标分别代入解析式计算出y1、y3、y2的值,然后比较大小即可.
解:∵点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,
∴y1=2,y2=﹣2,y3=﹣,
∴y2<y3<y1.
故选:B.
6.化简÷的结果是( )
A.x+3 B.x﹣3 C.3﹣x D.﹣6x
【分析】原式利用除法法则变形,约分即可得到结果.
解:原式=?
=x﹣3.
故选:B.
7.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
【分析】根据平行线四边形的判定方法对A进行判定;根据矩形的判定方法,对角线相等的平行四边形是矩形,则可对B进行判定;根据菱形的判定方法,对角线互相垂直的平行四边形是菱形,则可对C进行判定;根据正方形的判定方法,对角线互相垂直的矩形是正方形,则可对对D进行判定.
解:A、对角线互相平分的四边形是平行四边形,所以A选项为真命题;
B、对角线相等的平行四边形是矩形,所以B选项为假命题;
C、对角线互相垂直的平行四边形是菱形,所以C选项为假命题;
D、对角线互相垂直的矩形是正方形,所以D选项为假命题.
故选:A.
8.有一组数据:1,3,3,4,5,这组数据的众数为( )
A.1 B.3 C.4 D.5
【分析】根据众数的概念求解.
解:这组数据中3出现的次数最多,
故众数为3.
故选:B.
9.如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
【分析】由平行四边形的性质可得AD∥BC,AB=CD,可得∠DCE=∠BCE=∠DEC,可得DE=DC=AB,即可求AB的值.
解:∵四边形ABCD是平行四边形
∴AD∥BC,AB=CD,
∴∠DEC=∠BCE
∵CE平分∠BCD
∴∠DCE=∠BCE
∴∠DEC=∠DCE
∴DE=CD
∵AD=7,AE=3,
∴DE=4
∴AB=CD=DE=4,
故选:D.
10.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=,则折痕CE的长为( )
A.2 B. C. D.3
【分析】由点O是矩形ABCD的中心,E是AB上的点沿CE折叠后,点B恰好与点O重合,可求得∠BAC=30°,继而可得∠BCE=30°,继而求得折痕CE的长.
解:∵点O是矩形ABCD的中心,E是AB上的点沿CE折叠后,点B恰好与点O重合,
∴AC=2OC=2BC,∠B=90°,∠ACE=∠BCE,
∴sin∠BAC=,
∴∠BAC=30°,
∴∠ACB=90°﹣∠BAC=60°,
∴∠BCE=30°,
∴CE=
故选:A.
11.某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )
A. B.
C. D.
【分析】关键描述语是:“提前了4天完成任务”;等量关系为:原计划用时﹣实际用时=4,根据等量关系列式.
解:原计划用时,而实际工作效率提高后,
所用时间为.
方程应该表示为:.
故选:C.
12.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:
(1)∠E=22.5°;(2)∠AFC=112.5°;(3)∠ACE=135°;(4)AC=CE;(5)AD:CE=1:.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
【分析】AE平分∠DAC,AC是对角线,所以∠E=22.5°;∠AFC=112.5°;∠ACE=135°;AC=CE;均正确,而只有(5)无法确定.
解:在正方形ABCD中,∵AE平分∠DAC,AC是对角线,
∴∠CAF=∠E,∴AC=CE,
∴∠E=∠FAD=,
∠AFC=∠E+90°=112.5°
∠ACE=90°+45°=135°,
∵AC=CE,
∴AD:CE=1:.
故选:A.
二.填空题(共18分)
13.计算:= 1 .
【分析】因为分式的分母相同,所以只要将分母不变,分子相加即可.
解:=.故答案为1.
14.已知函数y=﹣x+3,当x= 3 时,函数值为0.
【分析】令y=0得到关于x的方程,从而可求得x的值.
解:当y=0时,﹣x+3=0,
解得:x=3.
故答案为:3.
15.某种流感病毒的直径是0.0000085cm,这个数据用科学记数法表示为 8.5×10﹣6 cm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000085=8.5×10﹣6.
故答案为:8.5×10﹣6.
16.九年级学生在进行跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得他们的平均成绩都是5.68米,甲的方差为0.3,乙的方差为0.4,那么成绩较为稳定的是 甲 (填“甲”或“乙”).
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解:∵甲的方差为0.3,乙的方差为0.4,0.3<0.4,
∴成绩较为稳定的是甲.
故答案为:甲.
17.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
【分析】首先根据菱形的对角线互相垂直平分,再利用勾股定理,求出BC的长是多少;然后再结合△ABC的面积的求法,求出菱形ABCD的高AE是多少即可.
解:∵四边形ABCD是菱形,
∴AC、BD互相垂直平分,
∴BO=BD=×8=4(cm),CO=AC=×6=3(cm),
在△BCO中,由勾股定理,可得
BC===5(cm)
∵AE⊥BC,
∴AE?BC=AC?BO,
∴AE===(cm),
即菱形ABCD的高AE为 cm.
故答案为:.
18.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k= 6 .
【分析】利用反比例函数图象上点的坐标,设F(a,),则根据F点为AB的中点得到B(a,),然后根据反比例函数系数k的几何意义,利用矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF得到k+k+6=a?,再解关于k的方程即可.
解:设F(a,),则B(a,),
因为矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF,
所以k+k+6=a?,
解得k=6.
故答案为6.
三、解答题(共66分)
19.计算:(π﹣2016)0+()﹣1﹣×|﹣3|
【分析】根据零指数幂、负整数指数幂的意义和绝对值的意义计算.
解:原式=1+3﹣2×3
=1+3﹣6
=﹣2.
20.解分式方程:+=2.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x+1+2x2﹣2x=2x2﹣2,
解得:x=3,
经检验x=3是分式方程的解.
21.先化简:÷(﹣),再从﹣2<x<3的范围内选取一个你喜欢的x值代入求值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,确定出x的值,代入计算即可求出值.
解:原式=÷=?=,
当x=2时,原式=4(x≠﹣1,0,1).
22.如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
【分析】根据平行四边形的定义得出四边形AEDF是平行四边形,再求出AE=DE,根据菱形的判定推出即可.
【解答】证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠EDA=∠BAD,
∴AE=DE,
∴四边形AEDF是菱形.
23. 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
每户丢弃废旧塑料袋(个) 频数(户) 频率
3 5 0.1
4 20 0.4
5 15 0.3
6 10 0.2
合计 50 1
(1)将统计表和条形统计图补充完整;
(2)求抽样的50户家庭这天丢弃废旧塑料袋的平均个数;
(3)根据抽样数据,估计该居民区10000户家庭这天丢弃的废旧塑料的个数.
【分析】(1)用总人数减去其他小组的人数即可得家庭丢弃塑料袋为5的小组的频数,除以总人数即可得到该组的频率;
(2)用加权平均数计算丢弃废旧塑料袋的平均个数即可;
(3)用样本的平均数估计总体的平均数即可.
解:(1)统计表和条形统计图补充如下:
家庭丢弃塑料袋是5个的:50﹣5﹣20﹣10=15,频率为:15÷50=0.3,,
(2)抽样的50户家庭这天丢弃废旧塑料袋的平均个数是:==4.6(个).
(3)∵样本数据的平均数是4.6,
∴该居民区10000户家庭这天丢弃的废旧塑料的平均个数是4.6.
于是4.6×10000=46000(个),
∴该居民区10000户家庭这天丢弃的废旧塑料的个数是46000个.
24.如图,直线y=x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积.
【分析】(1)由OB,PB的长,及P在第一象限,确定出P的坐标,根据P为反比例函数与直线的交点,得到P在反比例函数图象上,故将P的坐标代入反比例解析式中,即可求出k的值;
(2)根据待定系数法求得直线AC的解析式,令y=0求出对应x的值,即为A的横坐标,确定出A的坐标,即可求得AB,然后根据三角形的面积公式求得即可.
解:(1)∵OB=2,PB=4,且P在第一象限,
∴P(2,4),
由P在反比例函数y=上,
∴k=2×4=8,
∴反比例函数的解析式为y=;
(2)∵P(2,4)在直线y=x+b上,
∴4=+b,解得b=3,
∴直线y=x+3,
令y=0,解得:x=﹣6;
∴A(﹣6,0),
∴OA=6,
∴AB=8,
∴S△APB=AB?PB=×8×4=16.
25.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
【分析】(1)根据等腰三角形的性质,可得∠CAD=∠BAC,根据等式的性质,可得∠CAD+∠CAE=(∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(2)根据等腰直角三角形的性质,可得AD与CD的关系,根据正方形的判定,可得答案;
(3)根据勾股定理,可得AD的长,根据正方形周长公式,可得答案.
【解答】(1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=∠BAC=45°,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
=AB,AD=CD,
即AD=2,
AD=2,
正方形ADCE周长4AD=4×2=8.
26.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求点D的坐标;
(2)问直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请写出点M的坐标.
【分析】(1)设点C的坐标为(m,2),根据一次函数图象上点的坐标特征,代入直线解析式求解即可得到m的值,再根据矩形的长求出OA,然后写出点D的坐标即可.
(2)根据直线解析式求出△EBC为等腰直角三角形,根据等腰直角三角形的性质可得∠CEB=∠ECB=45°,再根据平行线的性质可得∠DCE=∠CEB=45°,然后判断出△PDC只能是以P、D为直角顶点的等腰直角三角形,再分①∠D=90°时,根据点P的横坐标与点D的横坐标相等,利用直线解析式求解即可;②∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,求出点P的横坐标,再代入直线解析式计算即可得解.
(3)根据平行四边形平行且对边相等,分DE、CE是对角线时,点M在x轴上,求出OM的长度,然后写出点M的坐标,CD是对角线时,求出平行四边形的中心的坐标,再求出点E关于中心的对称点,即为点M.
解:(1)设点C的坐标为(m,2),
∵点C在直线y=x﹣2上,
∴2=m﹣2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2).
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x﹣2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x﹣2得,y=﹣1,
∴点P1(1,﹣1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,
所以,点P2的横坐标为=,
把x=代入y=x﹣2得,y=,
所以,点P2(,),
综上所述,符合条件的点P的坐标为(1,﹣1)或(,).
(3)当y=0时,x﹣2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM﹣OE=3﹣2=1,
此时,点M的坐标为(﹣1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(,2),
设点M的坐标为(x,y),
则=,=2,
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(﹣1,0)或(5,0)或(3,4).
一、选择题(共12小题).
1.分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x=2 D.x=﹣2
2.在平面直角坐标系中,点(﹣3,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若方程=2+有增根,则a的值为( )
A.a=﹣4 B.a=4 C.a=3 D.a=2
4.直线y=2x﹣1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
6.化简÷的结果是( )
A.x+3 B.x﹣3 C.3﹣x D.﹣6x
7.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
8.有一组数据:1,3,3,4,5,这组数据的众数为( )
A.1 B.3 C.4 D.5
9.如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
10.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=,则折痕CE的长为( )
A.2 B. C. D.3
11.某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )
A. B.
C. D.
12.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:
(1)∠E=22.5°;(2)∠AFC=112.5°;(3)∠ACE=135°;(4)AC=CE;(5)AD:CE=1:.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共18分)
13.计算:= .
14.已知函数y=﹣x+3,当x= 时,函数值为0.
15.某种流感病毒的直径是0.0000085cm,这个数据用科学记数法表示为 cm.
16.九年级学生在进行跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得他们的平均成绩都是5.68米,甲的方差为0.3,乙的方差为0.4,那么成绩较为稳定的是 (填“甲”或“乙”).
17.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
18.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k= .
三、解答题(共66分)
19.计算:(π﹣2016)0+()﹣1﹣×|﹣3|
20.解分式方程:+=2.
21.先化简:÷(﹣),再从﹣2<x<3的范围内选取一个你喜欢的x值代入求值.
22.如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
23. 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
每户丢弃废旧塑料袋(个) 频数(户) 频率
3 5 0.1
4 20 0.4
5
6 10 0.2
合计 50 1
(1)将统计表和条形统计图补充完整;
(2)求抽样的50户家庭这天丢弃废旧塑料袋的平均个数;
(3)根据抽样数据,估计该居民区10000户家庭这天丢弃的废旧塑料的个数.
24.如图,直线y=x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积.
25.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
26.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求点D的坐标;
(2)问直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请写出点M的坐标.
参考答案
一、选择题(共12小题).
1.分式有意义,则x的取值范围是( )
A.x≠2 B.x≠﹣2 C.x=2 D.x=﹣2
解:根据题意得:x﹣2≠0,
解得:x≠2.
故选:A.
2.在平面直角坐标系中,点(﹣3,2)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
解:点(﹣3,2)所在的象限在第二象限.
故选:B.
3.若方程=2+有增根,则a的值为( )
A.a=﹣4 B.a=4 C.a=3 D.a=2
【分析】分式方程去分母转化为整式方程,由分式方程有增根得到x﹣4=0,求出x的值,代入整式方程计算即可求出a的值.
解:去分母得:x=2(x﹣4)+a,
由分式方程有增根,得到x﹣4=0,即x=4,
把x=4代入整式方程得:a=4.
故选:B.
4.直线y=2x﹣1不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据题目中的函数解析式和一次函数的性质可以解答本题.
解:∵y=2x﹣1,k=2>0,b=﹣1,
∴该函数经过第一、三、四象限,不经过第二象限,
故选:B.
5.若点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.y2<y1<y3
【分析】根据反比例函数图象上点的坐标特征,把三个点的坐标分别代入解析式计算出y1、y3、y2的值,然后比较大小即可.
解:∵点A(﹣1,y1),B(1,y2),C(3,y3)在反比例函数y=﹣的图象上,
∴y1=2,y2=﹣2,y3=﹣,
∴y2<y3<y1.
故选:B.
6.化简÷的结果是( )
A.x+3 B.x﹣3 C.3﹣x D.﹣6x
【分析】原式利用除法法则变形,约分即可得到结果.
解:原式=?
=x﹣3.
故选:B.
7.下列命题是真命题的是( )
A.对角线互相平分的四边形是平行四边形
B.对角线相等的四边形是矩形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是正方形
【分析】根据平行线四边形的判定方法对A进行判定;根据矩形的判定方法,对角线相等的平行四边形是矩形,则可对B进行判定;根据菱形的判定方法,对角线互相垂直的平行四边形是菱形,则可对C进行判定;根据正方形的判定方法,对角线互相垂直的矩形是正方形,则可对对D进行判定.
解:A、对角线互相平分的四边形是平行四边形,所以A选项为真命题;
B、对角线相等的平行四边形是矩形,所以B选项为假命题;
C、对角线互相垂直的平行四边形是菱形,所以C选项为假命题;
D、对角线互相垂直的矩形是正方形,所以D选项为假命题.
故选:A.
8.有一组数据:1,3,3,4,5,这组数据的众数为( )
A.1 B.3 C.4 D.5
【分析】根据众数的概念求解.
解:这组数据中3出现的次数最多,
故众数为3.
故选:B.
9.如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
【分析】由平行四边形的性质可得AD∥BC,AB=CD,可得∠DCE=∠BCE=∠DEC,可得DE=DC=AB,即可求AB的值.
解:∵四边形ABCD是平行四边形
∴AD∥BC,AB=CD,
∴∠DEC=∠BCE
∵CE平分∠BCD
∴∠DCE=∠BCE
∴∠DEC=∠DCE
∴DE=CD
∵AD=7,AE=3,
∴DE=4
∴AB=CD=DE=4,
故选:D.
10.如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=,则折痕CE的长为( )
A.2 B. C. D.3
【分析】由点O是矩形ABCD的中心,E是AB上的点沿CE折叠后,点B恰好与点O重合,可求得∠BAC=30°,继而可得∠BCE=30°,继而求得折痕CE的长.
解:∵点O是矩形ABCD的中心,E是AB上的点沿CE折叠后,点B恰好与点O重合,
∴AC=2OC=2BC,∠B=90°,∠ACE=∠BCE,
∴sin∠BAC=,
∴∠BAC=30°,
∴∠ACB=90°﹣∠BAC=60°,
∴∠BCE=30°,
∴CE=
故选:A.
11.某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )
A. B.
C. D.
【分析】关键描述语是:“提前了4天完成任务”;等量关系为:原计划用时﹣实际用时=4,根据等量关系列式.
解:原计划用时,而实际工作效率提高后,
所用时间为.
方程应该表示为:.
故选:C.
12.如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:
(1)∠E=22.5°;(2)∠AFC=112.5°;(3)∠ACE=135°;(4)AC=CE;(5)AD:CE=1:.
其中正确的有( )
A.5个 B.4个 C.3个 D.2个
【分析】AE平分∠DAC,AC是对角线,所以∠E=22.5°;∠AFC=112.5°;∠ACE=135°;AC=CE;均正确,而只有(5)无法确定.
解:在正方形ABCD中,∵AE平分∠DAC,AC是对角线,
∴∠CAF=∠E,∴AC=CE,
∴∠E=∠FAD=,
∠AFC=∠E+90°=112.5°
∠ACE=90°+45°=135°,
∵AC=CE,
∴AD:CE=1:.
故选:A.
二.填空题(共18分)
13.计算:= 1 .
【分析】因为分式的分母相同,所以只要将分母不变,分子相加即可.
解:=.故答案为1.
14.已知函数y=﹣x+3,当x= 3 时,函数值为0.
【分析】令y=0得到关于x的方程,从而可求得x的值.
解:当y=0时,﹣x+3=0,
解得:x=3.
故答案为:3.
15.某种流感病毒的直径是0.0000085cm,这个数据用科学记数法表示为 8.5×10﹣6 cm.
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000085=8.5×10﹣6.
故答案为:8.5×10﹣6.
16.九年级学生在进行跳远训练时,甲、乙两同学在相同条件下各跳10次,统计得他们的平均成绩都是5.68米,甲的方差为0.3,乙的方差为0.4,那么成绩较为稳定的是 甲 (填“甲”或“乙”).
【分析】根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解:∵甲的方差为0.3,乙的方差为0.4,0.3<0.4,
∴成绩较为稳定的是甲.
故答案为:甲.
17.如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形ABCD的高AE为 cm.
【分析】首先根据菱形的对角线互相垂直平分,再利用勾股定理,求出BC的长是多少;然后再结合△ABC的面积的求法,求出菱形ABCD的高AE是多少即可.
解:∵四边形ABCD是菱形,
∴AC、BD互相垂直平分,
∴BO=BD=×8=4(cm),CO=AC=×6=3(cm),
在△BCO中,由勾股定理,可得
BC===5(cm)
∵AE⊥BC,
∴AE?BC=AC?BO,
∴AE===(cm),
即菱形ABCD的高AE为 cm.
故答案为:.
18.如图,已知双曲线y=(x>0)经过矩形OABC边AB的中点F,交BC于点E,且四边形OEBF的面积为6,则k= 6 .
【分析】利用反比例函数图象上点的坐标,设F(a,),则根据F点为AB的中点得到B(a,),然后根据反比例函数系数k的几何意义,利用矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF得到k+k+6=a?,再解关于k的方程即可.
解:设F(a,),则B(a,),
因为矩形ABCO的面积=S△OCE+S△AOF+S四边形OEBF,
所以k+k+6=a?,
解得k=6.
故答案为6.
三、解答题(共66分)
19.计算:(π﹣2016)0+()﹣1﹣×|﹣3|
【分析】根据零指数幂、负整数指数幂的意义和绝对值的意义计算.
解:原式=1+3﹣2×3
=1+3﹣6
=﹣2.
20.解分式方程:+=2.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x+1+2x2﹣2x=2x2﹣2,
解得:x=3,
经检验x=3是分式方程的解.
21.先化简:÷(﹣),再从﹣2<x<3的范围内选取一个你喜欢的x值代入求值.
【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,确定出x的值,代入计算即可求出值.
解:原式=÷=?=,
当x=2时,原式=4(x≠﹣1,0,1).
22.如图,在△ABC中,AD平分∠BAC,过点D分别作DE∥AC、DF∥AB,分别交AB、AC于点E、F.求证:四边形AEDF是菱形.
【分析】根据平行四边形的定义得出四边形AEDF是平行四边形,再求出AE=DE,根据菱形的判定推出即可.
【解答】证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵DE∥AC,
∴∠EDA=∠CAD,
∴∠EDA=∠BAD,
∴AE=DE,
∴四边形AEDF是菱形.
23. 为了了解某居民区10000户家庭丢弃废旧塑料袋的情况,某环保组织在今年6月5日(世界环境日)这一天随机抽样调查了该小区50户家庭丢弃塑料袋的情况,制成如下统计表和条形统计图(如图)(均不完整).
每户丢弃废旧塑料袋(个) 频数(户) 频率
3 5 0.1
4 20 0.4
5 15 0.3
6 10 0.2
合计 50 1
(1)将统计表和条形统计图补充完整;
(2)求抽样的50户家庭这天丢弃废旧塑料袋的平均个数;
(3)根据抽样数据,估计该居民区10000户家庭这天丢弃的废旧塑料的个数.
【分析】(1)用总人数减去其他小组的人数即可得家庭丢弃塑料袋为5的小组的频数,除以总人数即可得到该组的频率;
(2)用加权平均数计算丢弃废旧塑料袋的平均个数即可;
(3)用样本的平均数估计总体的平均数即可.
解:(1)统计表和条形统计图补充如下:
家庭丢弃塑料袋是5个的:50﹣5﹣20﹣10=15,频率为:15÷50=0.3,,
(2)抽样的50户家庭这天丢弃废旧塑料袋的平均个数是:==4.6(个).
(3)∵样本数据的平均数是4.6,
∴该居民区10000户家庭这天丢弃的废旧塑料的平均个数是4.6.
于是4.6×10000=46000(个),
∴该居民区10000户家庭这天丢弃的废旧塑料的个数是46000个.
24.如图,直线y=x+b分别交x轴、y轴于点A、C,点P是直线AC与双曲线y=在第一象限内的交点,PB⊥x轴,垂足为点B,且OB=2,PB=4.
(1)求反比例函数的解析式;
(2)求△APB的面积.
【分析】(1)由OB,PB的长,及P在第一象限,确定出P的坐标,根据P为反比例函数与直线的交点,得到P在反比例函数图象上,故将P的坐标代入反比例解析式中,即可求出k的值;
(2)根据待定系数法求得直线AC的解析式,令y=0求出对应x的值,即为A的横坐标,确定出A的坐标,即可求得AB,然后根据三角形的面积公式求得即可.
解:(1)∵OB=2,PB=4,且P在第一象限,
∴P(2,4),
由P在反比例函数y=上,
∴k=2×4=8,
∴反比例函数的解析式为y=;
(2)∵P(2,4)在直线y=x+b上,
∴4=+b,解得b=3,
∴直线y=x+3,
令y=0,解得:x=﹣6;
∴A(﹣6,0),
∴OA=6,
∴AB=8,
∴S△APB=AB?PB=×8×4=16.
25.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2,求正方形ADCE周长.
【分析】(1)根据等腰三角形的性质,可得∠CAD=∠BAC,根据等式的性质,可得∠CAD+∠CAE=(∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(2)根据等腰直角三角形的性质,可得AD与CD的关系,根据正方形的判定,可得答案;
(3)根据勾股定理,可得AD的长,根据正方形周长公式,可得答案.
【解答】(1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=∠BAC=45°,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
=AB,AD=CD,
即AD=2,
AD=2,
正方形ADCE周长4AD=4×2=8.
26.如图,在平面直角坐标系xOy中,矩形ABCD的AB边在x轴上,AB=3,AD=2,经过点C的直线y=x﹣2与x轴、y轴分别交于点E、F.
(1)求点D的坐标;
(2)问直线y=x﹣2上是否存在点P,使得△PDC为等腰直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(3)在平面直角坐标系内确定点M,使得以点M、D、C、E为顶点的四边形是平行四边形,请写出点M的坐标.
【分析】(1)设点C的坐标为(m,2),根据一次函数图象上点的坐标特征,代入直线解析式求解即可得到m的值,再根据矩形的长求出OA,然后写出点D的坐标即可.
(2)根据直线解析式求出△EBC为等腰直角三角形,根据等腰直角三角形的性质可得∠CEB=∠ECB=45°,再根据平行线的性质可得∠DCE=∠CEB=45°,然后判断出△PDC只能是以P、D为直角顶点的等腰直角三角形,再分①∠D=90°时,根据点P的横坐标与点D的横坐标相等,利用直线解析式求解即可;②∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,求出点P的横坐标,再代入直线解析式计算即可得解.
(3)根据平行四边形平行且对边相等,分DE、CE是对角线时,点M在x轴上,求出OM的长度,然后写出点M的坐标,CD是对角线时,求出平行四边形的中心的坐标,再求出点E关于中心的对称点,即为点M.
解:(1)设点C的坐标为(m,2),
∵点C在直线y=x﹣2上,
∴2=m﹣2,
∴m=4,
即点C的坐标为(4,2),
∵四边形ABCD是矩形,
∴AB=CD=3,AD=BC=2,
∴点D的坐标为(1,2).
(2)存在.
∵△EBC为等腰直角三角形,
∴∠CEB=∠ECB=45°,
又∵DC∥AB,
∴∠DCE=∠CEB=45°,
∴△PDC只能是以P、D为直角顶点的等腰直角三角形,
如图,①当∠D=90°时,延长DA与直线y=x﹣2交于点P1,
∵点D的坐标为(1,2),
∴点P1的横坐标为1,
把x=1代入y=x﹣2得,y=﹣1,
∴点P1(1,﹣1);
②当∠DPC=90°时,作DC的垂直平分线与直线y=x﹣2的交点即为点P2,
所以,点P2的横坐标为=,
把x=代入y=x﹣2得,y=,
所以,点P2(,),
综上所述,符合条件的点P的坐标为(1,﹣1)或(,).
(3)当y=0时,x﹣2=0,
解得x=2,
∴OE=2,
∵以点M、D、C、E为顶点的四边形是平行四边形,
∴若DE是对角线,则EM=CD=3,
∴OM=EM﹣OE=3﹣2=1,
此时,点M的坐标为(﹣1,0),
若CE是对角线,则EM=CD=3,
OM=OE+EM=2+3=5,
此时,点M的坐标为(5,0),
若CD是对角线,则平行四边形的中心坐标为(,2),
设点M的坐标为(x,y),
则=,=2,
解得x=3,y=4,
此时,点M的坐标为(3,4),
综上所述,点M的坐标为(﹣1,0)或(5,0)或(3,4).
同课章节目录
