高一物理人教版必修2课件:7.8 机械能守恒定律 课件(共20张PPT)
文档属性
| 名称 | 高一物理人教版必修2课件:7.8 机械能守恒定律 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-27 07:26:35 | ||
图片预览








文档简介
第七章 机械能守恒定律
第八节 机械能守恒定律
人教版必修2
教学目标
1、知道什么是机械能,理解物体的动能和势能可以相互转化;
2、理解机械能守恒定律的内容和适用条件;
3、会判定具体问题中机械能是否守恒,能运用机械能守恒定律分析实际问题
释放钢球后,学生联系到伽利略理想实验中的判断,认识到若无空气阻力,应该摆到等高处,不会碰到鼻子。
一、导入新课
(1)复习巩固:
说出我们前面学过的三种功能关系
(2)实验:
(激疑)钢球用细绳悬起,请一同学 靠近,将钢球偏至同学鼻子处释放,摆回时,观察该同学反应。
一、动能和势能的相互转化
探究一:机械能中动能和势能能否相互转化
力做功的过程也是能量从一种形式转化为另一种形式的过程,物体的动能和势能总和称为机械能。
(1)同学们举出生活中的例子,说明动能和势能的相互转化
瀑布(自由落体):
过山车:
重力势能
动 能
荡秋千:
重力势能
撑杆跳高:
动能
(2)以自由落体运动的物体为例,从功能关系着手,解释动能和势能的变化原因。
根据合外力做功与动能的关系(即动能定理)得到
合外力即重力做正功,动能增加;
所以重力势能转化为动能
根据重力做功与重力势能的关系,得到重力做正功,重力势能减少;
二、机械能守恒定律
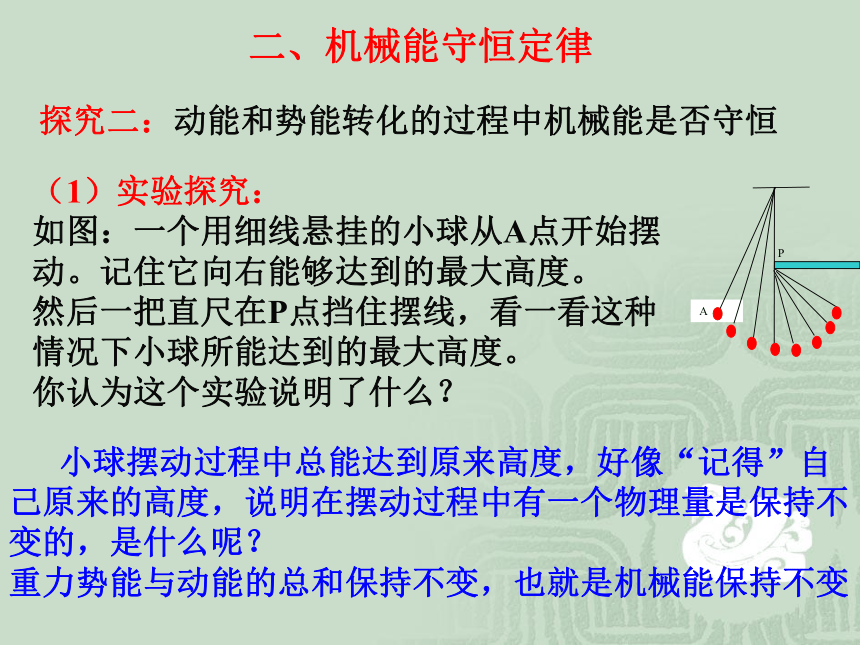
探究二:动能和势能转化的过程中机械能是否守恒
(1)实验探究:
如图:一个用细线悬挂的小球从A点开始摆动。记住它向右能够达到的最大高度。
然后一把直尺在P点挡住摆线,看一看这种情况下小球所能达到的最大高度。
你认为这个实验说明了什么?
小球摆动过程中总能达到原来高度,好像“记得”自己原来的高度,说明在摆动过程中有一个物理量是保持不变的,是什么呢?
重力势能与动能的总和保持不变,也就是机械能保持不变
A
P
研究方法:探究物理规律时,应该是由简单到复杂,逐步深入,先对简单的物理现象进行探究,然后加以推广深化。
情景设置:质量为m的物体自由下落过程中经过高度h1
的A点速度v1,高度h2的B点时速度为v2,不计空气阻
力,分析A、B两位置的机械能的关系。
由动能定理 WG=mv22/2-mv12/2= EK2-EK1
又 WG=mgh1-mgh2 = EP1-EP2
得到 EK2-EK1=EP1-EP2 ①
移项后,得 EP2+EK2 = EP1+EK1 ②
即 E2= E1
由于A,B是任意选择的,所以在整个过程中机械能守恒。
得出结论:自由下落过程物体机械能守恒
(2)理论分析:
探究三:机械能守恒是否有条件
举例分析:分析如下情况机械能是否守恒
例(1) 物体沿光滑斜面下滑
WG=
mv22-
mv12
WG=mgh1-mgh2
mv22
mv12
mgh1
mgh2
—
=
—
mv22
mv12
mgh1
mgh2
=
+
+
机械能守恒
例(2)探究二中例题计空气阻力时
mv22
mv12
WG—WF =
—
WG=mgh1-mgh2
mgh1
mgh2
mv22
mv12
WF
—
+
=
—
机械能不守恒
结论:只有重力做功时,总机械能守恒
+
mgh2
WF
mv22
+
=
mv12
mgh1
+
拓展分析:只有弹力做功时,能量如何变化,机械能是否守恒(注意研究对象)
如图,光滑小球套在水平杆上运动,C为原长处,从A到B过程中分析能量的变化,判定机械能是否守恒
分析 : WF= EK2-EK1
又 WF= EP1-EP2
则 EK2-EK1 = EP1-EP2
即 EP2+EK2=EP1+EK1
注意:弹簧的弹性势能转化为物体的动能
结论: 只有弹力做功时,系统机械能守恒(注意是系统)
机械能守恒的条件为系统内只有重力(或弹力)做功。
深入理解:对守恒条件的理解下列说法正确吗?
(1)只有重力(或弹力)做功意思是物体只受重力或弹力,不受其它力
(2)只有重力(或弹力)做功意思是除重力(或弹力)其它力都不做功
得出结论:
1、内容:在只有重力和弹力做功的物体系统内,动能和势能可以互相转化,而总的机械能保持不变
2、条件:系统内只有重力(或弹力)做功。
3、表达式: EP2+EK2=EP1+EK1 ( E2= E1)
机械能守恒定律
问题分析:一小球在真空中下落,有一质量相同的小球在粘滞性较大的液体中匀速下落,它们都因高度为h1的地方下落到h2的地方,在两种情况下,重力所做的功相等吗?重力势能各转化为什么形式的能?机械能守恒吗?
探究四:书本中的思考与讨论:
答案:重力所做的功相等,第一种情况重力势能转化为动能,机械能守恒。第一种情况重力势能转化为动能和内能,机械能不守恒。
从能量转化角度判定
拓展思考:
1、能的变化对应什么力做功。
除重力外的其它力做功等于机械能的变化
2、有其它方法判定机械能是否守恒吗?
探究五:探究机械能守恒定律解题的解题步骤及优点
例题:把一个小球用细绳悬挂起来,就成为一个摆(如图),摆长为l ,最大偏角为θ。小球运动到最低位置时的速度是多大?
三、机械能守恒定律的应用
分析:
1、小球受几个力,做功情况怎样?
2、小球运动过程中机械能守恒吗?
3、选取什么方法求解,能用前面学过的牛顿运动定律和运动学公式求解吗?
4、列公式求解前要注意什么?
(过程见课本)
A
l
C
O
对比总结优点:
机械能守恒定律不涉及运动过程中的加速度和时间,用它来处理问题要比牛顿定律方便;应用机械能守恒定律解决问题,只需考虑运动的始末状态,不必考虑两个状态之间过程的细节。因此一些难以用牛顿运动定律解决的问题,应用机械能守恒定律则易于解决。
总结解题的方法和步骤:
①.选取研究对象
②.根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒.
③.恰当地选取参考平面,确定研究对象在过程的初末时刻的机械能.
④.根据机械能守恒定律列方程,进行求解.
课堂练习
1、一辆小车静止在光滑的水平面上,小车立柱上固定一条长为L,拴有小球的细绳.小球由与悬点在同一水平面处释放.如下图所示,小球在摆动的过程中,不计阻力,则下列说法中正确的是 ( )
A.小 球的机械能守恒
B.小球的机械能不守恒
C.小球和小车的总机械能守恒
D.小球和小车的总机械能不守恒
BC
2、如图,一子弹以水平速度射入木块并留在其中,再与木块一起共同摆到最大高度的过程中,下列说法正确的是 ( )
A、子弹的机械能守恒。
B、木块的机械能守恒。
C、子弹和木块的总机械能守恒。
D、以上说法都不对
D
1、子弹射中木块的过程机械能不守恒
2、整体从最低位置摆到最高位置的过程机械能守恒
机械能条件:
除重力做功或弹簧弹力做功外,内力做功的代数和为零。
3、如图,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球;B处固定质量为m的小球,支架悬挂在O点,可绕过O点与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直,放手后开始运动.在无任何阻力的情况下,下列说法中正确的是 ( )
A.A球到达最低点时速度为零
B.A球机械能减小量等于B球机械能增加量
C.当支架从左向右回摆时,A球一定能回到起始高度
D.B球向左摆动所能达到的最高位置应高于A球开始运动的高度
o
A
B
2m
m
BCD
第八节 机械能守恒定律
人教版必修2
教学目标
1、知道什么是机械能,理解物体的动能和势能可以相互转化;
2、理解机械能守恒定律的内容和适用条件;
3、会判定具体问题中机械能是否守恒,能运用机械能守恒定律分析实际问题
释放钢球后,学生联系到伽利略理想实验中的判断,认识到若无空气阻力,应该摆到等高处,不会碰到鼻子。
一、导入新课
(1)复习巩固:
说出我们前面学过的三种功能关系
(2)实验:
(激疑)钢球用细绳悬起,请一同学 靠近,将钢球偏至同学鼻子处释放,摆回时,观察该同学反应。
一、动能和势能的相互转化
探究一:机械能中动能和势能能否相互转化
力做功的过程也是能量从一种形式转化为另一种形式的过程,物体的动能和势能总和称为机械能。
(1)同学们举出生活中的例子,说明动能和势能的相互转化
瀑布(自由落体):
过山车:
重力势能
动 能
荡秋千:
重力势能
撑杆跳高:
动能
(2)以自由落体运动的物体为例,从功能关系着手,解释动能和势能的变化原因。
根据合外力做功与动能的关系(即动能定理)得到
合外力即重力做正功,动能增加;
所以重力势能转化为动能
根据重力做功与重力势能的关系,得到重力做正功,重力势能减少;
二、机械能守恒定律
探究二:动能和势能转化的过程中机械能是否守恒
(1)实验探究:
如图:一个用细线悬挂的小球从A点开始摆动。记住它向右能够达到的最大高度。
然后一把直尺在P点挡住摆线,看一看这种情况下小球所能达到的最大高度。
你认为这个实验说明了什么?
小球摆动过程中总能达到原来高度,好像“记得”自己原来的高度,说明在摆动过程中有一个物理量是保持不变的,是什么呢?
重力势能与动能的总和保持不变,也就是机械能保持不变
A
P
研究方法:探究物理规律时,应该是由简单到复杂,逐步深入,先对简单的物理现象进行探究,然后加以推广深化。
情景设置:质量为m的物体自由下落过程中经过高度h1
的A点速度v1,高度h2的B点时速度为v2,不计空气阻
力,分析A、B两位置的机械能的关系。
由动能定理 WG=mv22/2-mv12/2= EK2-EK1
又 WG=mgh1-mgh2 = EP1-EP2
得到 EK2-EK1=EP1-EP2 ①
移项后,得 EP2+EK2 = EP1+EK1 ②
即 E2= E1
由于A,B是任意选择的,所以在整个过程中机械能守恒。
得出结论:自由下落过程物体机械能守恒
(2)理论分析:
探究三:机械能守恒是否有条件
举例分析:分析如下情况机械能是否守恒
例(1) 物体沿光滑斜面下滑
WG=
mv22-
mv12
WG=mgh1-mgh2
mv22
mv12
mgh1
mgh2
—
=
—
mv22
mv12
mgh1
mgh2
=
+
+
机械能守恒
例(2)探究二中例题计空气阻力时
mv22
mv12
WG—WF =
—
WG=mgh1-mgh2
mgh1
mgh2
mv22
mv12
WF
—
+
=
—
机械能不守恒
结论:只有重力做功时,总机械能守恒
+
mgh2
WF
mv22
+
=
mv12
mgh1
+
拓展分析:只有弹力做功时,能量如何变化,机械能是否守恒(注意研究对象)
如图,光滑小球套在水平杆上运动,C为原长处,从A到B过程中分析能量的变化,判定机械能是否守恒
分析 : WF= EK2-EK1
又 WF= EP1-EP2
则 EK2-EK1 = EP1-EP2
即 EP2+EK2=EP1+EK1
注意:弹簧的弹性势能转化为物体的动能
结论: 只有弹力做功时,系统机械能守恒(注意是系统)
机械能守恒的条件为系统内只有重力(或弹力)做功。
深入理解:对守恒条件的理解下列说法正确吗?
(1)只有重力(或弹力)做功意思是物体只受重力或弹力,不受其它力
(2)只有重力(或弹力)做功意思是除重力(或弹力)其它力都不做功
得出结论:
1、内容:在只有重力和弹力做功的物体系统内,动能和势能可以互相转化,而总的机械能保持不变
2、条件:系统内只有重力(或弹力)做功。
3、表达式: EP2+EK2=EP1+EK1 ( E2= E1)
机械能守恒定律
问题分析:一小球在真空中下落,有一质量相同的小球在粘滞性较大的液体中匀速下落,它们都因高度为h1的地方下落到h2的地方,在两种情况下,重力所做的功相等吗?重力势能各转化为什么形式的能?机械能守恒吗?
探究四:书本中的思考与讨论:
答案:重力所做的功相等,第一种情况重力势能转化为动能,机械能守恒。第一种情况重力势能转化为动能和内能,机械能不守恒。
从能量转化角度判定
拓展思考:
1、能的变化对应什么力做功。
除重力外的其它力做功等于机械能的变化
2、有其它方法判定机械能是否守恒吗?
探究五:探究机械能守恒定律解题的解题步骤及优点
例题:把一个小球用细绳悬挂起来,就成为一个摆(如图),摆长为l ,最大偏角为θ。小球运动到最低位置时的速度是多大?
三、机械能守恒定律的应用
分析:
1、小球受几个力,做功情况怎样?
2、小球运动过程中机械能守恒吗?
3、选取什么方法求解,能用前面学过的牛顿运动定律和运动学公式求解吗?
4、列公式求解前要注意什么?
(过程见课本)
A
l
C
O
对比总结优点:
机械能守恒定律不涉及运动过程中的加速度和时间,用它来处理问题要比牛顿定律方便;应用机械能守恒定律解决问题,只需考虑运动的始末状态,不必考虑两个状态之间过程的细节。因此一些难以用牛顿运动定律解决的问题,应用机械能守恒定律则易于解决。
总结解题的方法和步骤:
①.选取研究对象
②.根据研究对象所经历的物理过程,进行受力,做功分析,判断机械能是否守恒.
③.恰当地选取参考平面,确定研究对象在过程的初末时刻的机械能.
④.根据机械能守恒定律列方程,进行求解.
课堂练习
1、一辆小车静止在光滑的水平面上,小车立柱上固定一条长为L,拴有小球的细绳.小球由与悬点在同一水平面处释放.如下图所示,小球在摆动的过程中,不计阻力,则下列说法中正确的是 ( )
A.小 球的机械能守恒
B.小球的机械能不守恒
C.小球和小车的总机械能守恒
D.小球和小车的总机械能不守恒
BC
2、如图,一子弹以水平速度射入木块并留在其中,再与木块一起共同摆到最大高度的过程中,下列说法正确的是 ( )
A、子弹的机械能守恒。
B、木块的机械能守恒。
C、子弹和木块的总机械能守恒。
D、以上说法都不对
D
1、子弹射中木块的过程机械能不守恒
2、整体从最低位置摆到最高位置的过程机械能守恒
机械能条件:
除重力做功或弹簧弹力做功外,内力做功的代数和为零。
3、如图,长度相同的三根轻杆构成一个正三角形支架,在A处固定质量为2m的小球;B处固定质量为m的小球,支架悬挂在O点,可绕过O点与支架所在平面相垂直的固定轴转动.开始时OB与地面相垂直,放手后开始运动.在无任何阻力的情况下,下列说法中正确的是 ( )
A.A球到达最低点时速度为零
B.A球机械能减小量等于B球机械能增加量
C.当支架从左向右回摆时,A球一定能回到起始高度
D.B球向左摆动所能达到的最高位置应高于A球开始运动的高度
o
A
B
2m
m
BCD
