高中人教版物理必2课件:6.4 万有引力理论的成就课件(共 29张PPT)
文档属性
| 名称 | 高中人教版物理必2课件:6.4 万有引力理论的成就课件(共 29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 678.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-27 00:00:00 | ||
图片预览








文档简介
6.4
万有引力理论的成就
美国的阿波罗8号从月球返回时,当地面控制中心问是谁在驾驶时,指令长这样回答:“我想是牛顿在驾驶”。为什么会这样说呢?万有引力定律的发现有着重要的物理意义:他对天文学的发展具有深远的影响,他把地面上的物体运动的规律和天体运动的规律统一起来,对科学文化的发展起到了积极的推动作用,解放了人们的思想,给人们探索自然的奥秘建立了极大的信心,人们有能力理解天地间的各种事物。这节课我们就将通过几个万有引力定律的应用的事例来窥探一斑。这节课我们一起学习---万有引力理论的伟大成就。
导入新课
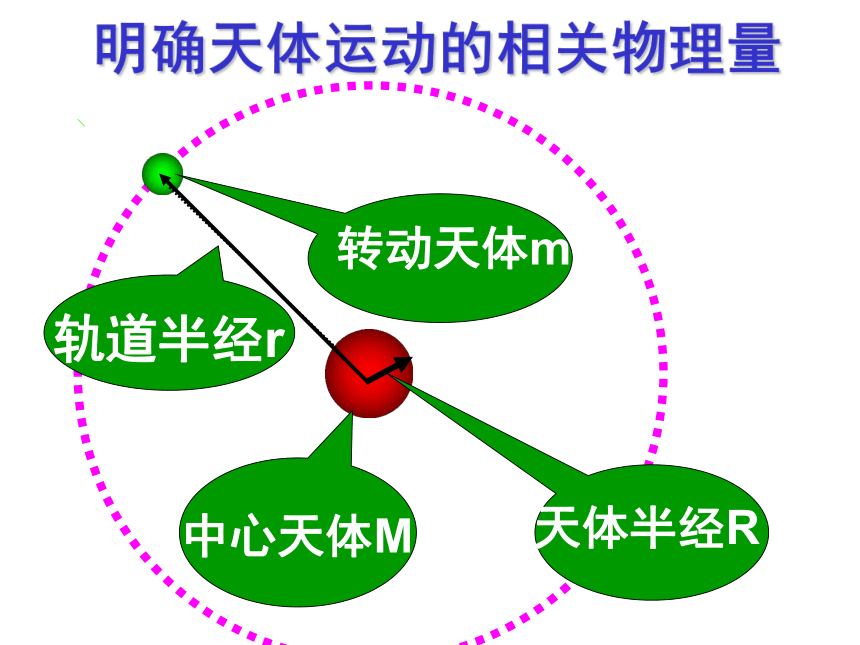
中心天体M
转动天体m
轨道半经r
明确天体运动的相关物理量
天体半经R
一、科学真是迷人
阅读·思考
1.著名文学家马克·吐温曾满怀激情的说:“科学真是迷人,根据零星的事实,增添一些猜想,竟能获得那么多收获!”对此你是怎么理解的?
自然界中万物是有规律可循的,我们要敢于探索,大胆猜想,一旦发现一个规律,我们将有意想不到的收获。
2.卡文迪许在实验室里“测量”几个铅球之间的作用力,测出了引力常量G的值,从而“称量”出了地球的质量。测出G后,是怎样“称量”地球的质量?
在地球表面,mg=GMm/R2,从而有M=gR2/G,只要测出G,便可“称量”地球的质量。
同步练习
1.设地面附近的重力加速度g
=
9.8m/s2,地球半径R
=
6400km
,引力常量G=6.67×10-11Nm2/kg2,试估算地球的质量。
2.已知月球的质量是7.3×1022kg,半径是1.7×103km,月球表面的自由落体加速度有多大?这对宇航员在月球表面的行动会产生什么样的影响?
万有引力近似等于重力,由GMm/r2=mg月知,
g月约为地球表面加速度g的六分之一,在月球上人感觉很轻,习惯在地球表面行走的人,在月球表面是跳跃前进的。
一、科学真是迷人
二、计算天体的质量
引导·思考
二、计算天体的质量
阅读·思考
1.应用万有引力定律求解天体质量的基本思路是什么?
根据环绕天体的运动情况,结合万有引力充当向心力,进而列方程求解
2.求解天体质量的方程依据是什么?
天体之间存在着相互作用的万有引力,而行星(或卫星)都在绕恒星(或行星)做近似圆周的运动,而物体做圆周运动时合力充当向心力,故对于天体所做的圆周运动的动力学方程只能是万有引力充当向心力
1、天体实际做何运动?而我们通常可认为做什么运动?
天体实际上沿椭圆轨道运动,通常认为天体在做匀速圆周运动
2、描述匀速圆周运动的物理量有哪些?
线速度v,角速度ω,周期T三个物理量
3、向心力有几种表达方式?
(1)F向心=mv2/r,(2)F向心=mω2·r,(3)F向心=4mπ2r/T2
4、应用天体运动的动力学方程——万有引力充当向心力
求出的天体质量有几种表达式?各是什么?各有什么特点?幻灯片
8
5、应用此方法能否求出环绕天体的质量?
二、计算天体的质量
从以上各式的推导过程可知,利用此法只能求出中心天体的质量,因为环绕天体的质量同时出现在方程的两边已被约去。
二、计算天体的质量
以地球绕太阳运动为例:
1.若已知地球绕太阳做匀速圆周运动的半径r和周期T。
根据万有引力等于向心力,即GMm/r2=m4π2r/T2,可求得太阳质量M=4π2r3/GT2。
2.若已知地球绕太阳做匀速圆周运动的半径r和线速度v。
由于地球受到的万有引力充当向心力,即GMm/r2=mv2/r,得太阳的质量为M=v2r/G。
3.若已知地球绕太阳圆周运动的速度v和周期T。
由于地球受到的引力等于其所需的向心力,可知:GMm/r2=m·v·2π/T,以及GMm/r2=mv2/r.两式相除消去r,解得M=V3T/2πG。
3.不同行星与太阳的距离r和围绕太阳公转的周期T都是各不相同的,但是不同行星的r,T计算出来的太阳质量必须是一样的!这里得到的计算太阳质量的公式能否保证这一点?
二、计算天体的质量
同步练习
4.能否利用人造卫星的相关信息测量地球质量?
某人造地球卫星沿圆形轨道运行,轨道半径是6.8×103km,周期是5.6×103s。试从这些数据估算地球的质量。
5.93×1024kg
应用万有引力计算某个天体的质量,有两种方法:
1.知道这个天体表面的重力加速度g,根据公式M=gR2/G求解;
2.知道这个天体一颗行星或卫星运动的周期T和半径r,利用公式M=4π2r3/GT2求解。
二、计算天体的质量
课堂小结
2.利用天体的卫星来求天体的密度
设卫星绕天体运动的轨迹半径为r,周期为T,天体半径为R,则可列方程GMm/r2=m4π2r/T2和
M=
得
1.利用天体表面的重力加速度求天体的自身密度。
由mg=GMm/R2和M=
得
思考:天体的质量求出来了,能否求天体的平均密度?如何求?写出其计算表达式。
三、计算天体的密度
ρ
ρ
=
3g/4GR
ρ
ρ
=
四、发现未知天体
阅读·讨论
1、应用万有引力定律除可估算天体质量外,还可以在天文学上有何应用?
还可以用来发现未知的天体。
4.人们用类似的方法又发现了哪颗天体?
3.笔尖下发现的行星是哪一颗行星?
海王星
2、发现未知天体的基本方法.
当一个已知天体的实际轨道和理论计算的轨道之间有较大的误差时,说明该天体周围可能还有未知的天体给这个行星施加引力,然后应用万有引力定律,结合对天体的观测资料,便计算出了另一天体的轨道,进而在计算出的位置观察新的天体。
哈雷彗星的“按时回归”,冥王星等等。
五、同步练习
5、利用下列哪组数据可以计算出地球的质量(
)
A:已知地球的半径r和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和线速度V
D:已知卫星围绕地球运动的线速度V和周期T
6、某行星的卫星,在靠近行星表面轨道上运行.若要
计算行星的密度,唯一要测量出的物理量是(
)
A.
行星的半径.
B.
卫星的半径.
C.
卫星运行的线速度
D.卫星运行的周期.
ABCD
D
五、同步练习
7.下列说法正确的是(
)
天王星是人们由万有引力定律计算其轨道而发现的
B.海王星及冥王星是人们依据万有引力定律计算其轨道而发现的
C.天王星的运行轨道偏离,其原因是由于天王星受到轨道外面的其它行星的引力作用
D.以上说法均不正确
BC
8.密封舱在离月球表面112km的空中沿圆形轨道运行,周期是120.5min,月球的半径是1740km,根据这些数据计算月球的质量和平均密度。
M=7.19×1022kg
ρ=3.26×103kg/m3
六、课堂总结
本节课我们学习了地球质量测定——天体质量测定——天体轨道的演算推测,直观地了解了万有引力定律在人类认识自然界奥秘中发挥的巨大作用!
理论来源于实践,反过来又可以指导实践。所以在人们后来的探索前进道路上,仍旧难忘牛顿等前辈科学家的功勋。
一.求解天体运动问题的基本思路
1.将行星(或卫星)的运动看成
是匀速圆周运动.
2.万有引力充当向心力F引=F向.或在球体表面附近F引=G重
知识梳理
一.基本思路
二.应用一
天体质量的计算
方法一.
已知天体的球体半径R和球体表面重力加速度g.求天体的质量
基本思路
二.应用一
天体质量的计算
方法二.
已知行星(或卫星)的周期公转周期T、轨道半径r,可求出中心天体的质量M(但不能求出行星或卫星的质量m)
二.应用一
天体质量的计算
基本思路
二.应用二
天体密度的计算
基本思路:
根据上面两种方式算出中心天体的质量M,结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度
二.应用二
天体密度的计算
二.应用二
天体密度的计算
当r≈R时
二.应用三
发现未知天体
基本思路.
当一个已知行星的实际轨道和理论计算的轨道之间有较大的误差时,说明还有未知的天体给这个行星施加引力.然后应用万有引力定律,结合对天体的观测资料,便计算出了另一天体的轨道,进而在计算出的位置观察新的天体。
理论指导实践
二.应用三
发现未知天体
mg
F向心
F
O
引力F的一个分力是物体需要的向心力,另一个分力是物体的重力。考虑地球自转时,物体在赤道上所受重力最小,在两极时重力最大。
一般情况下认为引力等于重力,g和物体重力的变化可以忽略不计。
引力和
重力的
关系
思考:
根据所学的知识你能解释为什么可以不考虑地球自转的影响?
R
M
G
θ
m
ω
r
F
向
F引
结论:向心力远小于重力,万有引力大小近似等于重力。因此不考虑(忽略)地球自转的影响。
明确卫星的v、ω、T与r的关系
基本思路.
万有引力充当向心力F引=F向.
万有引力理论的成就
美国的阿波罗8号从月球返回时,当地面控制中心问是谁在驾驶时,指令长这样回答:“我想是牛顿在驾驶”。为什么会这样说呢?万有引力定律的发现有着重要的物理意义:他对天文学的发展具有深远的影响,他把地面上的物体运动的规律和天体运动的规律统一起来,对科学文化的发展起到了积极的推动作用,解放了人们的思想,给人们探索自然的奥秘建立了极大的信心,人们有能力理解天地间的各种事物。这节课我们就将通过几个万有引力定律的应用的事例来窥探一斑。这节课我们一起学习---万有引力理论的伟大成就。
导入新课
中心天体M
转动天体m
轨道半经r
明确天体运动的相关物理量
天体半经R
一、科学真是迷人
阅读·思考
1.著名文学家马克·吐温曾满怀激情的说:“科学真是迷人,根据零星的事实,增添一些猜想,竟能获得那么多收获!”对此你是怎么理解的?
自然界中万物是有规律可循的,我们要敢于探索,大胆猜想,一旦发现一个规律,我们将有意想不到的收获。
2.卡文迪许在实验室里“测量”几个铅球之间的作用力,测出了引力常量G的值,从而“称量”出了地球的质量。测出G后,是怎样“称量”地球的质量?
在地球表面,mg=GMm/R2,从而有M=gR2/G,只要测出G,便可“称量”地球的质量。
同步练习
1.设地面附近的重力加速度g
=
9.8m/s2,地球半径R
=
6400km
,引力常量G=6.67×10-11Nm2/kg2,试估算地球的质量。
2.已知月球的质量是7.3×1022kg,半径是1.7×103km,月球表面的自由落体加速度有多大?这对宇航员在月球表面的行动会产生什么样的影响?
万有引力近似等于重力,由GMm/r2=mg月知,
g月约为地球表面加速度g的六分之一,在月球上人感觉很轻,习惯在地球表面行走的人,在月球表面是跳跃前进的。
一、科学真是迷人
二、计算天体的质量
引导·思考
二、计算天体的质量
阅读·思考
1.应用万有引力定律求解天体质量的基本思路是什么?
根据环绕天体的运动情况,结合万有引力充当向心力,进而列方程求解
2.求解天体质量的方程依据是什么?
天体之间存在着相互作用的万有引力,而行星(或卫星)都在绕恒星(或行星)做近似圆周的运动,而物体做圆周运动时合力充当向心力,故对于天体所做的圆周运动的动力学方程只能是万有引力充当向心力
1、天体实际做何运动?而我们通常可认为做什么运动?
天体实际上沿椭圆轨道运动,通常认为天体在做匀速圆周运动
2、描述匀速圆周运动的物理量有哪些?
线速度v,角速度ω,周期T三个物理量
3、向心力有几种表达方式?
(1)F向心=mv2/r,(2)F向心=mω2·r,(3)F向心=4mπ2r/T2
4、应用天体运动的动力学方程——万有引力充当向心力
求出的天体质量有几种表达式?各是什么?各有什么特点?幻灯片
8
5、应用此方法能否求出环绕天体的质量?
二、计算天体的质量
从以上各式的推导过程可知,利用此法只能求出中心天体的质量,因为环绕天体的质量同时出现在方程的两边已被约去。
二、计算天体的质量
以地球绕太阳运动为例:
1.若已知地球绕太阳做匀速圆周运动的半径r和周期T。
根据万有引力等于向心力,即GMm/r2=m4π2r/T2,可求得太阳质量M=4π2r3/GT2。
2.若已知地球绕太阳做匀速圆周运动的半径r和线速度v。
由于地球受到的万有引力充当向心力,即GMm/r2=mv2/r,得太阳的质量为M=v2r/G。
3.若已知地球绕太阳圆周运动的速度v和周期T。
由于地球受到的引力等于其所需的向心力,可知:GMm/r2=m·v·2π/T,以及GMm/r2=mv2/r.两式相除消去r,解得M=V3T/2πG。
3.不同行星与太阳的距离r和围绕太阳公转的周期T都是各不相同的,但是不同行星的r,T计算出来的太阳质量必须是一样的!这里得到的计算太阳质量的公式能否保证这一点?
二、计算天体的质量
同步练习
4.能否利用人造卫星的相关信息测量地球质量?
某人造地球卫星沿圆形轨道运行,轨道半径是6.8×103km,周期是5.6×103s。试从这些数据估算地球的质量。
5.93×1024kg
应用万有引力计算某个天体的质量,有两种方法:
1.知道这个天体表面的重力加速度g,根据公式M=gR2/G求解;
2.知道这个天体一颗行星或卫星运动的周期T和半径r,利用公式M=4π2r3/GT2求解。
二、计算天体的质量
课堂小结
2.利用天体的卫星来求天体的密度
设卫星绕天体运动的轨迹半径为r,周期为T,天体半径为R,则可列方程GMm/r2=m4π2r/T2和
M=
得
1.利用天体表面的重力加速度求天体的自身密度。
由mg=GMm/R2和M=
得
思考:天体的质量求出来了,能否求天体的平均密度?如何求?写出其计算表达式。
三、计算天体的密度
ρ
ρ
=
3g/4GR
ρ
ρ
=
四、发现未知天体
阅读·讨论
1、应用万有引力定律除可估算天体质量外,还可以在天文学上有何应用?
还可以用来发现未知的天体。
4.人们用类似的方法又发现了哪颗天体?
3.笔尖下发现的行星是哪一颗行星?
海王星
2、发现未知天体的基本方法.
当一个已知天体的实际轨道和理论计算的轨道之间有较大的误差时,说明该天体周围可能还有未知的天体给这个行星施加引力,然后应用万有引力定律,结合对天体的观测资料,便计算出了另一天体的轨道,进而在计算出的位置观察新的天体。
哈雷彗星的“按时回归”,冥王星等等。
五、同步练习
5、利用下列哪组数据可以计算出地球的质量(
)
A:已知地球的半径r和地球表面的重力加速度g
B:已知卫星围绕地球运动的轨道半径r和周期T
C:已知卫星围绕地球运动的轨道半径r和线速度V
D:已知卫星围绕地球运动的线速度V和周期T
6、某行星的卫星,在靠近行星表面轨道上运行.若要
计算行星的密度,唯一要测量出的物理量是(
)
A.
行星的半径.
B.
卫星的半径.
C.
卫星运行的线速度
D.卫星运行的周期.
ABCD
D
五、同步练习
7.下列说法正确的是(
)
天王星是人们由万有引力定律计算其轨道而发现的
B.海王星及冥王星是人们依据万有引力定律计算其轨道而发现的
C.天王星的运行轨道偏离,其原因是由于天王星受到轨道外面的其它行星的引力作用
D.以上说法均不正确
BC
8.密封舱在离月球表面112km的空中沿圆形轨道运行,周期是120.5min,月球的半径是1740km,根据这些数据计算月球的质量和平均密度。
M=7.19×1022kg
ρ=3.26×103kg/m3
六、课堂总结
本节课我们学习了地球质量测定——天体质量测定——天体轨道的演算推测,直观地了解了万有引力定律在人类认识自然界奥秘中发挥的巨大作用!
理论来源于实践,反过来又可以指导实践。所以在人们后来的探索前进道路上,仍旧难忘牛顿等前辈科学家的功勋。
一.求解天体运动问题的基本思路
1.将行星(或卫星)的运动看成
是匀速圆周运动.
2.万有引力充当向心力F引=F向.或在球体表面附近F引=G重
知识梳理
一.基本思路
二.应用一
天体质量的计算
方法一.
已知天体的球体半径R和球体表面重力加速度g.求天体的质量
基本思路
二.应用一
天体质量的计算
方法二.
已知行星(或卫星)的周期公转周期T、轨道半径r,可求出中心天体的质量M(但不能求出行星或卫星的质量m)
二.应用一
天体质量的计算
基本思路
二.应用二
天体密度的计算
基本思路:
根据上面两种方式算出中心天体的质量M,结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度
二.应用二
天体密度的计算
二.应用二
天体密度的计算
当r≈R时
二.应用三
发现未知天体
基本思路.
当一个已知行星的实际轨道和理论计算的轨道之间有较大的误差时,说明还有未知的天体给这个行星施加引力.然后应用万有引力定律,结合对天体的观测资料,便计算出了另一天体的轨道,进而在计算出的位置观察新的天体。
理论指导实践
二.应用三
发现未知天体
mg
F向心
F
O
引力F的一个分力是物体需要的向心力,另一个分力是物体的重力。考虑地球自转时,物体在赤道上所受重力最小,在两极时重力最大。
一般情况下认为引力等于重力,g和物体重力的变化可以忽略不计。
引力和
重力的
关系
思考:
根据所学的知识你能解释为什么可以不考虑地球自转的影响?
R
M
G
θ
m
ω
r
F
向
F引
结论:向心力远小于重力,万有引力大小近似等于重力。因此不考虑(忽略)地球自转的影响。
明确卫星的v、ω、T与r的关系
基本思路.
万有引力充当向心力F引=F向.
