高中人教版物理必2课件:6.5 宇宙航行课件课件(共82 张PPT)
文档属性
| 名称 | 高中人教版物理必2课件:6.5 宇宙航行课件课件(共82 张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-27 11:01:12 | ||
图片预览









文档简介
人造卫星、宇宙飞船
第五节
宇宙航行
我国发射的人造卫星类型
想一想:卫星是怎样发射上去的呢?
V0
以平抛运动为模型的推理过程
牛顿人造卫星原理图
一、人造卫星
究竟怎样才能发射一颗卫星呢?
牛顿的猜想
方法一:万有引力提供物体作圆周运动的向心力
方法二:在地面附近,重力提供物体作圆周运动的向心力
问题一:以多大的速度抛出这个物体,它才会绕地球表面运动,不会落下来?(已知G=6.67×10-11Nm2/kg2
,
地球质量M=5.89×1024kg,
地球半径R=6400km)
(若已知地球表面重力加速度g=9.8m/s2,R=6400km)
r
R
设地球和卫星的质量分别为M和m,卫星到地心的距离为r,求卫星运动的线速度v?
由F引=F向得到
v
F引
M
m
当r=R时即近地卫星
,由
可得v=7.9km/s
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗人造地球卫星简称
由此可见,人造地球卫星运行遵循的规律是:卫星绕地球做圆周运动,地球对卫星的引力就是向心力。
人造卫星。
(一)人造卫星
想一想:卫星运动快慢跟什么有关呢?
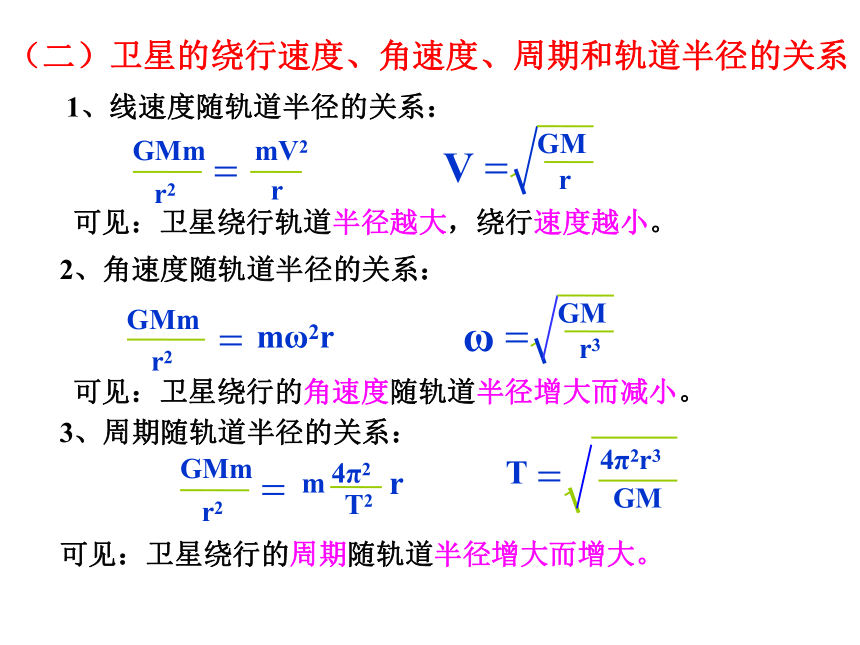
(二)卫星的绕行速度、角速度、周期和轨道半径的关系
1、线速度随轨道半径的关系:
r
mV2
r2
GMm
=
r
GM
V
=
可见:卫星绕行轨道半径越大,绕行速度越小。
2、角速度随轨道半径的关系:
mω2r
r2
GMm
=
r3
GM
ω
=
可见:卫星绕行的角速度随轨道半径增大而减小。
3、周期随轨道半径的关系:
T2
m
r2
GMm
=
4π2
r
GM
T
=
4π2r3
可见:卫星绕行的周期随轨道半径增大而增大。
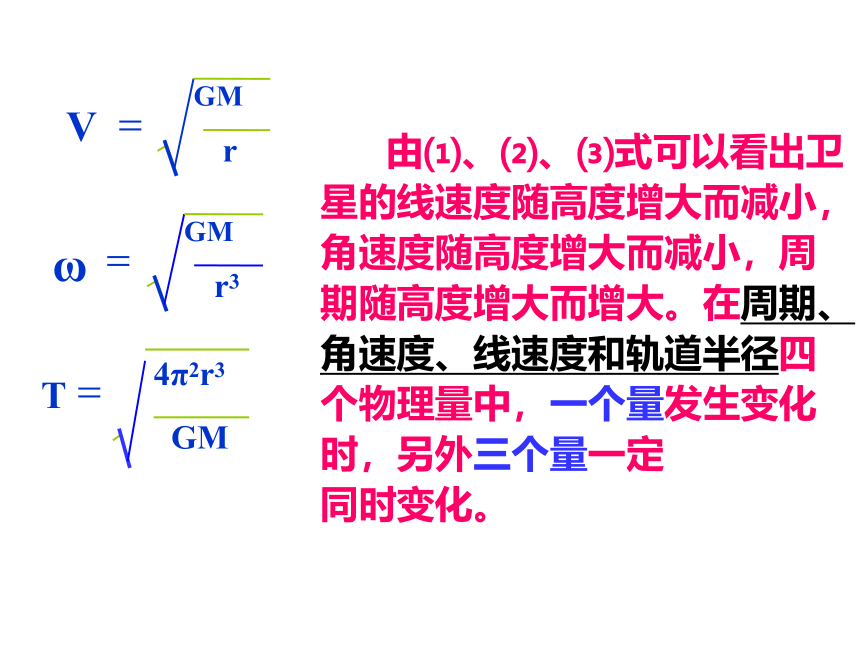
由⑴、⑵、⑶式可以看出卫星的线速度随高度增大而减小,角速度随高度增大而减小,周期随高度增大而增大。在周期、角速度、线速度和轨道半径四个物理量中,一个量发生变化时,另外三个量一定
同时变化。
r
GM
V
=
r3
GM
ω
=
GM
T
=
4π2r3
各种各样的卫星……
F
赤道平面
北
南
东
西
F
思考:卫星的轨道
人造地球卫星的运行轨道
卫星绕地球做匀速圆周运动时,是地球的引力提供向心力,卫星受到地球的引力方向指向地心,而做圆周运动的向心力方向始终指向圆心,所以卫星圆周运动的圆心和地球的地心重合。这样就存在三类人造地球卫星轨道:
①赤道轨道,卫星轨道在赤道平面,
卫星始终处于赤道上方;
②极地轨道,卫星轨道平面与赤道
平面垂直,卫星通过两极上空;
③一般轨道,卫星轨道和赤道成
一定角度。
地球
二、人造卫星
1.
轨道中心
地心
2.
________
提供向心力
万有引力
3.
r越大,T
_____,V
_____,
ω
_____,an
_______
越大
越小
越小
越小
对于靠近地面的卫星,可以认为此时的r近似等于地球半径R,把r用地球半径R代入,可以求出
这就是人造地球卫星在地面附近绕地球做匀速圆周运动所必须具有的速度,叫做第一宇宙速度。
二.
宇宙速度
1.第一宇宙速度(环绕速度)
第一宇宙速度的另一表达式
根据地球表面(忽略自转)物体的重力近似于对物体的万有引力可得:
对第一宇宙速度的理解:
1.上式对其它天体也适用,R为天体半径,
M为天
体质量,
g为天体表面的重力加度,G为引力常量.
2.v1为发射卫星的最小发射速度,又是卫星进入轨道后最大线速度(也叫运行速度).
?
人造卫星的发射速度与运行速度
1、发射速度是指被发射物在地面附近离开发射装置时的速度,并且一旦发射就再也没有补充能量,被发射物仅依靠自身的初动能克服地球引力做功上升一定高度,进入运行轨道.因卫星上升过程中要克服引力和空气阻力(在大气层中时)做功消耗动能,所以卫星越高,发射速度越大。
2、运行速度是指卫星在进入轨道后绕地球做匀速圆周运动的线速度,根据
可知,卫星越高轨道半径越大,卫星运行速度(环绕速度)就越小,近
地卫星可认为v发=v运
,其它较高卫星的v发>v运.
r
V发
V运
故:
牢记:第一宇宙速度v1=7.9km/s是近地卫星的发射速度和运行速度,是人造卫星的最小发射速度最大运行速度.
向高轨道发射卫星与发射近地卫星相比哪个难度大?哪个需要的发射速度大?为什么?
高轨道卫星与近地卫星相比哪个运行速度大?为什么?
注意:人造卫星的发射速度与运行速度是两个不同的概念
运行速度
指卫星在稳定的轨道上绕地球转动的线速度
发射速度
指被发射物体离开地面时的速度
V1=7.9km/s
(第一宇宙速度)
最小发射速度
最大运行速度
人造卫星的r大,
需要的v发射大;而v运行却小
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,而小于11.2km/s,它绕地球运动的轨迹是椭圆。
当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
2.第二宇宙速度(脱离速度)
卫星挣脱地球束缚的最小发射速度
达到第二宇宙速度的物体还受到太阳的引力
如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
3.第三宇宙速度(逃逸速度)
卫星挣脱太阳束缚的最小发射速度
三个宇宙速度
V=16.7km/s
对地球(1)v1=7.9km/s
是人造卫星的最小发射速度和最大环绕速度。若7.9km/s卫星绕地球做椭圆运动。
2、第二宇宙速度(逃逸速度):
v
2=11.2km/s
是卫星挣脱地球束缚的最小发射速度
3、第三宇宙速度(逃逸速度):v3
=16.7km/s是卫星挣脱太阳束缚的最小发射速度
知识梳理:
1.第一宇宙速度(环绕速度)
:
(对任何天体都适用)
二、宇宙速度
归纳总结:
发射速度v
运动情况
v﹤7.9km/s
v=7.9km/s
7.9km/s
﹤
v
﹤11.2km/s
11.2km/s
v
﹤16.7km/s
16.7km/s
v
第二宇宙速度
第一宇宙速度
第三宇宙速度
物体落回地面
物体在地面附近绕地
球做匀速圆周运动
物体绕地球运转,运
动轨迹是椭圆。
物体绕太阳运动
物体飞出太阳系
第5节
宇
宙
航
行
地球同步卫星:相对于地面静止且与地球自转具有相同周期的卫星叫地球同步卫星,又叫通讯卫星。
三、地球同步卫星(通讯卫星)
特点:
1、运行方向与地球自转方向一致
2、角速度
,周期(T=24h)与地球相同,是一个恒量.
3、轨道平面与赤道平面平行
4、距地面高度一定
(h=3.6×107m),环绕速度大小一定。
即轨道平面一定,高度一定,运动快慢一定
why?
所谓地球同步卫星是指与地球自转同步,相对于地面静止的人造卫星.
w
1、为什么必须在赤道平面上?
因为:(1)同步卫星与地球自转同步必须自西向东转;
(2)万有引力提供做向心力,圆心就是地心.
所以:同步卫星轨道平面必定在赤道平面上.
2、为什么高度一定?
O
万有引力提供做向心力
由:
得:
把T=86400s,M=5.98x1024kg,R=6.37x106m得h=3.58x107m
地球同步卫星的特点
(1)周期与地球自转周期相同(T=24h),角速度与地球自转角速度也相同
(2)只能在赤道平面内绕地球转动
(3)距地面高度一定
同步卫星
同步卫星发射时的轨道
想一想:哪一个是同步卫星?
思考:如何利用同步卫星实现全球通讯?
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
h≈0
r=6.4×106m
v=7.9km/s
T=84分钟
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
四、梦想成真
探索宇宙的奥秘,奔向广阔而遥远的太空,是人类自古以来的梦想,现在真的“梦想成真”了
人类航天始祖----万户
人类航天的始祖是我国明朝的万户。在15世纪的我国明朝早期,一位名叫“万户”的官员,在一把椅子的背后装上47支火箭。当然,那是当时能买到的最大的火箭。他自己坐在椅子上,并用绳子绑紧。两手则各拿一个大风筝。然后他要仆人将47支火箭同时点燃,想借用火箭的力量把他推向空中。这是美国人罗伯特·吉姆在1945年出版的《火箭与喷射》一书中的叙述。英国、德国和前苏联的一些火箭专家,在他们的著作中也提到或引用了这件事。可见,万户是世界上公认的“第一个尝试利用火箭进行飞行的人”。为表彰他的功绩,国际天文联合会将月球上的一座环形山命名为“万户”。
1957年10月,苏联发射
第一颗人造地球卫星。
1961年4月12日苏联空军少校
加加林乘坐东方一号载人飞
船进入太空,实现了人类进
入太空的梦想。
1969年7月20日,阿波罗
11号将人类送上了月球。
四、梦想成真
梦想成真:
谁为人类迈向太空提供科学思想
19世纪中叶俄罗斯学者齐奥尔科夫斯基(喷气推进的多级火箭)
第一颗人造地球卫星何时何地发射成功
1957年10月4日苏联
第一艘载人飞船何时何地发射成功
1961年4月12日
苏联
加加林
东方一号载人飞船
人类何时登上月球
1969年7月16日9时32分,美国
阿波罗11号升空,19日进入月球轨道,20日下午4时17分着陆,10时56分阿姆斯特朗踏上月面
对个人来说,这不过是小小的一步,但对人类而言,却是巨大飞跃
人类遨游太空回顾
蒂托
2001年4月30日,第一位太空游客、美国人蒂托(中)快乐地进入国际空间站,开始了他为期一周的太空观光生活。太空旅游的开辟使得普通人也能够像宇航员一样畅游星际之间。
1970年4月24日我国
第一颗人造卫星升空
我国的航天成就
2007年10月24日嫦娥
一号月球探测器发射成功
第5节
宇
宙
航
行
1992年我国载人航天工程正式启动
2003年10月15日
神舟五号
杨利伟
2005年10月12日
神舟六号
费俊龙聂海胜
2008年9月25日
神舟七号
翟志刚刘伯明
景海鹏
4.1990年3月,紫金山天文台将该台发现的2752号小行星命名为“吴健雄星”。将其看作球形,直径为32km,它的密度和地球密度相近。若在此小行星上发射一颗卫星环绕
其表面附近运转。求此卫星的环绕速度。(地球半径取6400km)
解:
因
故
又
即此卫星的环绕速度为20m/s
故
又
5.已知地球的质量约为月球质量的81倍,地球半径于约为月球半径的4倍,在地球上发射近地卫星的环绕速度为7.9km/s,周期为84min,那么在月球上发射一颗近地
卫星的环绕速度多大?它的周期多大?
解:
因
即
又因
故
又因
故
对地球(1)v1=7.9km/s
是人造卫星的最小发射速度和最大环绕速度。若7.9km/s卫星绕地球做椭圆运动。
2、第二宇宙速度(逃逸速度):
v
2=11.2km/s
是卫星挣脱地球束缚的最小发射速度
3、第三宇宙速度(逃逸速度):v3
=16.7km/s是卫星挣脱太阳束缚的最小发射速度
三、同步卫星(通讯卫星)
小结:
1.第一宇宙速度(环绕速度)
:
(对任何天体都适用)
一、人造卫星
二、宇宙速度
五、人造卫星的超重和失重
1、发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2、沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
天平
弹簧秤测重力
液体压强计
3.关于人造地球卫星及其中物体的超重、
失重问题,下列说法正确的是(
)
A.在发射过程中向上加速时
产生超重现象
B.在降落过程中向下减速时产
生失重现象
C.进入轨道时作匀速圆周运动,
产生失重现象
D.失重是由于地球对卫星内物
体的作用力减小而引起的
A
C
·
思考:人造卫星在低轨道上运行,要想让其
在高轨道上运行,应采取什么措施?
在低轨道上加速,使其沿椭圆轨道运行,当行至椭圆轨道的远点处时再次加速,即可使其沿
高轨道运行。………..
六、变轨问题
v
F引
1
2
v2
F引
L
使卫星进入更高轨道做圆周运动
v2
v3
v
v’
非远地点变轨
向高轨卫星的发射
卫星的回收
v
F引
v’
F引’
A
B
写出A位置与B位置的向心力方程?
例3、如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A、在轨道3上的速率大
于1上的速率
B、在轨道3上的角速度
小于1上的角速度
C、在轨道2上经过Q点时
的速率等于在轨道3上经过Q点时的速率
D、在轨道1上经过P点时的加速度等于在轨道2上
经过P点时的加速度
Q
P
2
·
3
1
BD
“嫦娥奔月”
图(视频)16
练习1:2007年10月24日“嫦娥一号”卫星星箭分离,卫星进入绕
地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨
道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→
地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度
为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆
轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示。(
)
A.“嫦娥一号”由⑤到⑥需加速、由⑦到⑧需减速
B.发射“嫦娥一号”的速度必须达到第三宇宙速度
C.在绕月圆轨道上,卫星周期与卫星质量有关
D.卫星受月球的引力与它到月球中心距离的平方成反比
E.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
练习2.
2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示。
若月球半径为R,试写出月球表面重力加速度的表达式。
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
七、对接问题:宇宙飞船与空间站的对接
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何登到空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
不行,因为飞船加速后做离心运动会偏离原来的圆轨道而无法与空间站对接。飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,便可实现对接,如图所示.
空间站
飞船
例:在太空中有两飞行器a、b,它们在绕地球的同一圆形轨道上同向运行,a在前b在后,它都配有能沿运动方向向前或向后喷气的发动机,现要想b
尽快追上a
并完成对接,b应采取的措施是(
)
A、沿运动方向喷气
B、先沿运动方向喷气,后运动沿反方向喷气
C、沿运动反方向喷气
D、先沿运动反方向喷气,后沿运动方向喷气
B
八、“双星”问题
“双星”是由两颗绕着共同的中心旋转的恒星组成。对于其中一颗来说,另一颗就是其“伴星”。
1.两颗恒星均围绕共同的旋转中心做匀速圆周运动。
2.两恒星之间万有引力分别提供了两恒星的向心力,即两颗恒星受到的向心力大小相等。
3.两颗恒星与旋转中心时刻三点共线,即两颗恒星角速度相同,周期相同。
双星运动的特点:
确定双星的旋转中心:
质量
m
越大,旋转半径越小,离旋转中心越近。
F引
mg0
Fn
九、重力、万有引力与向心力的关系
F引
FN
F引
FN
人造地球卫星:
两极的物体:
赤道上的物体:
近地卫星:
地球表面的物体
(与地球具有相同的ω)
即:
即:
14\15
例:设同步卫星离地心距离为r,运行速率为v1,加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则(
)
A.
B.
C.
D.
AD
1、在某行星上用弹簧来秤测量某一物体的重力。在赤道上测量的示数比在两极处测量的示数小1/10,若该行星一昼夜的运行时间为T,万有引力常量为G,则这颗行星的密度为多少?
30π/GT
2
2、如果地球自转加快,地球赤道上物体的重量将发生怎样的变化?
1.4小时
当自转周期等于多少时可使赤道上的物体飘起来?
减小
连续物或卫星群的判断问题
9:根据观察,在土星外层有一个环带,该环带有星云等物质构成,为了判断环带是土星的连续物还是小卫星群。可测出环中各层的线速度v与该层到土星中心的距离R之间的关系,从而加以确定。对此下列判断正确的是:(
)
A.若v与R成正比,则环带是连续物
B.若v与R成正比,则环带是小卫星群
C.若v与R成反比,则环带是连续物
D.若v与R成反比,则环带是小卫星群
AD
12.1990年3月,紫金山天文台将1965年9月20日发现的一颗小行星命名为吴健雄星,直径为32km,如果该行星的密度与地球相同,则对该小行星来说,其上物体的第一宇宙速度约为多少?
(已知地球半径为6400km,地球上第一宇宙速度为7.9km/s)
解:由于"吴健雄星"的密度与地球的密度相近,
所以有M地/(4πr3地/3)=M吴/(4πr3吴/3)
即M吴=M地(r吴/r地)3
代入环绕速度公式得
v=√GM吴/r吴=√GM地r吴2/r地3=r吴v1/r地=20m/s
13.恒星演化发展到一定阶段,可能成为恒星世界的“侏儒”——中子星.中子星的半径较小,一般在7
km—20
km,但它的密度大得惊人.若某中子星的半径为10
km,密度为1.2×1017kg/m3,那么该中子星上的第一宇宙速度约为(
)
A.7.9
km/s
B.16.7
km/s
C.2.9×104
km/s
D.5.8×104
km/s
第五节
宇宙航行
我国发射的人造卫星类型
想一想:卫星是怎样发射上去的呢?
V0
以平抛运动为模型的推理过程
牛顿人造卫星原理图
一、人造卫星
究竟怎样才能发射一颗卫星呢?
牛顿的猜想
方法一:万有引力提供物体作圆周运动的向心力
方法二:在地面附近,重力提供物体作圆周运动的向心力
问题一:以多大的速度抛出这个物体,它才会绕地球表面运动,不会落下来?(已知G=6.67×10-11Nm2/kg2
,
地球质量M=5.89×1024kg,
地球半径R=6400km)
(若已知地球表面重力加速度g=9.8m/s2,R=6400km)
r
R
设地球和卫星的质量分别为M和m,卫星到地心的距离为r,求卫星运动的线速度v?
由F引=F向得到
v
F引
M
m
当r=R时即近地卫星
,由
可得v=7.9km/s
在地球上抛出的物体,当它的速度足够大时,物体就永远不会落到地面上,它将围绕地球旋转,成为一颗人造地球卫星简称
由此可见,人造地球卫星运行遵循的规律是:卫星绕地球做圆周运动,地球对卫星的引力就是向心力。
人造卫星。
(一)人造卫星
想一想:卫星运动快慢跟什么有关呢?
(二)卫星的绕行速度、角速度、周期和轨道半径的关系
1、线速度随轨道半径的关系:
r
mV2
r2
GMm
=
r
GM
V
=
可见:卫星绕行轨道半径越大,绕行速度越小。
2、角速度随轨道半径的关系:
mω2r
r2
GMm
=
r3
GM
ω
=
可见:卫星绕行的角速度随轨道半径增大而减小。
3、周期随轨道半径的关系:
T2
m
r2
GMm
=
4π2
r
GM
T
=
4π2r3
可见:卫星绕行的周期随轨道半径增大而增大。
由⑴、⑵、⑶式可以看出卫星的线速度随高度增大而减小,角速度随高度增大而减小,周期随高度增大而增大。在周期、角速度、线速度和轨道半径四个物理量中,一个量发生变化时,另外三个量一定
同时变化。
r
GM
V
=
r3
GM
ω
=
GM
T
=
4π2r3
各种各样的卫星……
F
赤道平面
北
南
东
西
F
思考:卫星的轨道
人造地球卫星的运行轨道
卫星绕地球做匀速圆周运动时,是地球的引力提供向心力,卫星受到地球的引力方向指向地心,而做圆周运动的向心力方向始终指向圆心,所以卫星圆周运动的圆心和地球的地心重合。这样就存在三类人造地球卫星轨道:
①赤道轨道,卫星轨道在赤道平面,
卫星始终处于赤道上方;
②极地轨道,卫星轨道平面与赤道
平面垂直,卫星通过两极上空;
③一般轨道,卫星轨道和赤道成
一定角度。
地球
二、人造卫星
1.
轨道中心
地心
2.
________
提供向心力
万有引力
3.
r越大,T
_____,V
_____,
ω
_____,an
_______
越大
越小
越小
越小
对于靠近地面的卫星,可以认为此时的r近似等于地球半径R,把r用地球半径R代入,可以求出
这就是人造地球卫星在地面附近绕地球做匀速圆周运动所必须具有的速度,叫做第一宇宙速度。
二.
宇宙速度
1.第一宇宙速度(环绕速度)
第一宇宙速度的另一表达式
根据地球表面(忽略自转)物体的重力近似于对物体的万有引力可得:
对第一宇宙速度的理解:
1.上式对其它天体也适用,R为天体半径,
M为天
体质量,
g为天体表面的重力加度,G为引力常量.
2.v1为发射卫星的最小发射速度,又是卫星进入轨道后最大线速度(也叫运行速度).
?
人造卫星的发射速度与运行速度
1、发射速度是指被发射物在地面附近离开发射装置时的速度,并且一旦发射就再也没有补充能量,被发射物仅依靠自身的初动能克服地球引力做功上升一定高度,进入运行轨道.因卫星上升过程中要克服引力和空气阻力(在大气层中时)做功消耗动能,所以卫星越高,发射速度越大。
2、运行速度是指卫星在进入轨道后绕地球做匀速圆周运动的线速度,根据
可知,卫星越高轨道半径越大,卫星运行速度(环绕速度)就越小,近
地卫星可认为v发=v运
,其它较高卫星的v发>v运.
r
V发
V运
故:
牢记:第一宇宙速度v1=7.9km/s是近地卫星的发射速度和运行速度,是人造卫星的最小发射速度最大运行速度.
向高轨道发射卫星与发射近地卫星相比哪个难度大?哪个需要的发射速度大?为什么?
高轨道卫星与近地卫星相比哪个运行速度大?为什么?
注意:人造卫星的发射速度与运行速度是两个不同的概念
运行速度
指卫星在稳定的轨道上绕地球转动的线速度
发射速度
指被发射物体离开地面时的速度
V1=7.9km/s
(第一宇宙速度)
最小发射速度
最大运行速度
人造卫星的r大,
需要的v发射大;而v运行却小
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,而小于11.2km/s,它绕地球运动的轨迹是椭圆。
当物体的速度大于或等于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。我们把这个速度叫第二宇宙速度。达到第二宇宙速度的物体还受到太阳的引力。
2.第二宇宙速度(脱离速度)
卫星挣脱地球束缚的最小发射速度
达到第二宇宙速度的物体还受到太阳的引力
如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。我们把这个速度叫第三宇宙速度。
3.第三宇宙速度(逃逸速度)
卫星挣脱太阳束缚的最小发射速度
三个宇宙速度
V=16.7km/s
对地球(1)v1=7.9km/s
是人造卫星的最小发射速度和最大环绕速度。若7.9km/s
2、第二宇宙速度(逃逸速度):
v
2=11.2km/s
是卫星挣脱地球束缚的最小发射速度
3、第三宇宙速度(逃逸速度):v3
=16.7km/s是卫星挣脱太阳束缚的最小发射速度
知识梳理:
1.第一宇宙速度(环绕速度)
:
(对任何天体都适用)
二、宇宙速度
归纳总结:
发射速度v
运动情况
v﹤7.9km/s
v=7.9km/s
7.9km/s
﹤
v
﹤11.2km/s
11.2km/s
v
﹤16.7km/s
16.7km/s
v
第二宇宙速度
第一宇宙速度
第三宇宙速度
物体落回地面
物体在地面附近绕地
球做匀速圆周运动
物体绕地球运转,运
动轨迹是椭圆。
物体绕太阳运动
物体飞出太阳系
第5节
宇
宙
航
行
地球同步卫星:相对于地面静止且与地球自转具有相同周期的卫星叫地球同步卫星,又叫通讯卫星。
三、地球同步卫星(通讯卫星)
特点:
1、运行方向与地球自转方向一致
2、角速度
,周期(T=24h)与地球相同,是一个恒量.
3、轨道平面与赤道平面平行
4、距地面高度一定
(h=3.6×107m),环绕速度大小一定。
即轨道平面一定,高度一定,运动快慢一定
why?
所谓地球同步卫星是指与地球自转同步,相对于地面静止的人造卫星.
w
1、为什么必须在赤道平面上?
因为:(1)同步卫星与地球自转同步必须自西向东转;
(2)万有引力提供做向心力,圆心就是地心.
所以:同步卫星轨道平面必定在赤道平面上.
2、为什么高度一定?
O
万有引力提供做向心力
由:
得:
把T=86400s,M=5.98x1024kg,R=6.37x106m得h=3.58x107m
地球同步卫星的特点
(1)周期与地球自转周期相同(T=24h),角速度与地球自转角速度也相同
(2)只能在赤道平面内绕地球转动
(3)距地面高度一定
同步卫星
同步卫星发射时的轨道
想一想:哪一个是同步卫星?
思考:如何利用同步卫星实现全球通讯?
h=3.6×107m
r=4.2×107m
v=3km/s
T=24h
h=3.8×108m
r≈3.8×108m
v=1km/s
T=27天
h≈0
r=6.4×106m
v=7.9km/s
T=84分钟
同步卫星
近地卫星
月球
近地卫星、同步卫星、月球三者比较
四、梦想成真
探索宇宙的奥秘,奔向广阔而遥远的太空,是人类自古以来的梦想,现在真的“梦想成真”了
人类航天始祖----万户
人类航天的始祖是我国明朝的万户。在15世纪的我国明朝早期,一位名叫“万户”的官员,在一把椅子的背后装上47支火箭。当然,那是当时能买到的最大的火箭。他自己坐在椅子上,并用绳子绑紧。两手则各拿一个大风筝。然后他要仆人将47支火箭同时点燃,想借用火箭的力量把他推向空中。这是美国人罗伯特·吉姆在1945年出版的《火箭与喷射》一书中的叙述。英国、德国和前苏联的一些火箭专家,在他们的著作中也提到或引用了这件事。可见,万户是世界上公认的“第一个尝试利用火箭进行飞行的人”。为表彰他的功绩,国际天文联合会将月球上的一座环形山命名为“万户”。
1957年10月,苏联发射
第一颗人造地球卫星。
1961年4月12日苏联空军少校
加加林乘坐东方一号载人飞
船进入太空,实现了人类进
入太空的梦想。
1969年7月20日,阿波罗
11号将人类送上了月球。
四、梦想成真
梦想成真:
谁为人类迈向太空提供科学思想
19世纪中叶俄罗斯学者齐奥尔科夫斯基(喷气推进的多级火箭)
第一颗人造地球卫星何时何地发射成功
1957年10月4日苏联
第一艘载人飞船何时何地发射成功
1961年4月12日
苏联
加加林
东方一号载人飞船
人类何时登上月球
1969年7月16日9时32分,美国
阿波罗11号升空,19日进入月球轨道,20日下午4时17分着陆,10时56分阿姆斯特朗踏上月面
对个人来说,这不过是小小的一步,但对人类而言,却是巨大飞跃
人类遨游太空回顾
蒂托
2001年4月30日,第一位太空游客、美国人蒂托(中)快乐地进入国际空间站,开始了他为期一周的太空观光生活。太空旅游的开辟使得普通人也能够像宇航员一样畅游星际之间。
1970年4月24日我国
第一颗人造卫星升空
我国的航天成就
2007年10月24日嫦娥
一号月球探测器发射成功
第5节
宇
宙
航
行
1992年我国载人航天工程正式启动
2003年10月15日
神舟五号
杨利伟
2005年10月12日
神舟六号
费俊龙聂海胜
2008年9月25日
神舟七号
翟志刚刘伯明
景海鹏
4.1990年3月,紫金山天文台将该台发现的2752号小行星命名为“吴健雄星”。将其看作球形,直径为32km,它的密度和地球密度相近。若在此小行星上发射一颗卫星环绕
其表面附近运转。求此卫星的环绕速度。(地球半径取6400km)
解:
因
故
又
即此卫星的环绕速度为20m/s
故
又
5.已知地球的质量约为月球质量的81倍,地球半径于约为月球半径的4倍,在地球上发射近地卫星的环绕速度为7.9km/s,周期为84min,那么在月球上发射一颗近地
卫星的环绕速度多大?它的周期多大?
解:
因
即
又因
故
又因
故
对地球(1)v1=7.9km/s
是人造卫星的最小发射速度和最大环绕速度。若7.9km/s
2、第二宇宙速度(逃逸速度):
v
2=11.2km/s
是卫星挣脱地球束缚的最小发射速度
3、第三宇宙速度(逃逸速度):v3
=16.7km/s是卫星挣脱太阳束缚的最小发射速度
三、同步卫星(通讯卫星)
小结:
1.第一宇宙速度(环绕速度)
:
(对任何天体都适用)
一、人造卫星
二、宇宙速度
五、人造卫星的超重和失重
1、发射和回收阶段
发射
加速上升
超重
回收
减速下降
超重
2、沿圆轨道正常运行
只受重力
a
=
g
完全失重
与重力有关的现象全部消失
天平
弹簧秤测重力
液体压强计
3.关于人造地球卫星及其中物体的超重、
失重问题,下列说法正确的是(
)
A.在发射过程中向上加速时
产生超重现象
B.在降落过程中向下减速时产
生失重现象
C.进入轨道时作匀速圆周运动,
产生失重现象
D.失重是由于地球对卫星内物
体的作用力减小而引起的
A
C
·
思考:人造卫星在低轨道上运行,要想让其
在高轨道上运行,应采取什么措施?
在低轨道上加速,使其沿椭圆轨道运行,当行至椭圆轨道的远点处时再次加速,即可使其沿
高轨道运行。………..
六、变轨问题
v
F引
1
2
v2
F引
L
使卫星进入更高轨道做圆周运动
v2
v3
v
v’
非远地点变轨
向高轨卫星的发射
卫星的回收
v
F引
v’
F引’
A
B
写出A位置与B位置的向心力方程?
例3、如图所示,发射同步卫星时,先将卫星发射至近地圆轨道1,然后经点火使其沿椭圆轨道2运行;最后再次点火将其送入同步圆轨道3。轨道1、2相切于P点,2、3相切于Q点。当卫星分别在1、2、3上正常运行时,以下说法正确的是(
)
A、在轨道3上的速率大
于1上的速率
B、在轨道3上的角速度
小于1上的角速度
C、在轨道2上经过Q点时
的速率等于在轨道3上经过Q点时的速率
D、在轨道1上经过P点时的加速度等于在轨道2上
经过P点时的加速度
Q
P
2
·
3
1
BD
“嫦娥奔月”
图(视频)16
练习1:2007年10月24日“嫦娥一号”卫星星箭分离,卫星进入绕
地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨
道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→
地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度
为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆
轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示。(
)
A.“嫦娥一号”由⑤到⑥需加速、由⑦到⑧需减速
B.发射“嫦娥一号”的速度必须达到第三宇宙速度
C.在绕月圆轨道上,卫星周期与卫星质量有关
D.卫星受月球的引力与它到月球中心距离的平方成反比
E.在绕月圆轨道上,卫星受地球的引力大于受月球的引力
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
练习2.
2007年10月24日,“嫦娥一号”卫星星箭分离,卫星进入绕地轨道。在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→修正轨道④→地月转移轨道⑤。11月5日11时,当卫星经过距月球表面高度为h的A点时,再经三次变轨:12小时椭圆轨道⑥→3.5小时椭圆轨道⑦→最后进入周期为T的极月圆轨道⑧
,如图所示。
若月球半径为R,试写出月球表面重力加速度的表达式。
①
②
③
近地变轨
轨道修正
转移轨道
④
⑤
⑥
⑦
⑧
发射
七、对接问题:宇宙飞船与空间站的对接
空间站实际上就是一个载有人的人造卫星,那么,地球上的人如何登到空间站,空间站上的人又如何返回地面?这些活动都需要通过宇宙飞船来完成,这就存在一个宇宙飞船与空间站对接的问题。
思考:能否把宇宙飞船先发射到空间站的同一轨道上,再通过加速去追上空间站实现对接呢?
不行,因为飞船加速后做离心运动会偏离原来的圆轨道而无法与空间站对接。飞船首先在比空间站低的轨道运行,当运行到适当位置时,再加速运行到一个椭圆轨道。通过控制轨道使飞船跟空间站恰好同时运行到两轨道的相切点,便可实现对接,如图所示.
空间站
飞船
例:在太空中有两飞行器a、b,它们在绕地球的同一圆形轨道上同向运行,a在前b在后,它都配有能沿运动方向向前或向后喷气的发动机,现要想b
尽快追上a
并完成对接,b应采取的措施是(
)
A、沿运动方向喷气
B、先沿运动方向喷气,后运动沿反方向喷气
C、沿运动反方向喷气
D、先沿运动反方向喷气,后沿运动方向喷气
B
八、“双星”问题
“双星”是由两颗绕着共同的中心旋转的恒星组成。对于其中一颗来说,另一颗就是其“伴星”。
1.两颗恒星均围绕共同的旋转中心做匀速圆周运动。
2.两恒星之间万有引力分别提供了两恒星的向心力,即两颗恒星受到的向心力大小相等。
3.两颗恒星与旋转中心时刻三点共线,即两颗恒星角速度相同,周期相同。
双星运动的特点:
确定双星的旋转中心:
质量
m
越大,旋转半径越小,离旋转中心越近。
F引
mg0
Fn
九、重力、万有引力与向心力的关系
F引
FN
F引
FN
人造地球卫星:
两极的物体:
赤道上的物体:
近地卫星:
地球表面的物体
(与地球具有相同的ω)
即:
即:
14\15
例:设同步卫星离地心距离为r,运行速率为v1,加速度为a1,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,则(
)
A.
B.
C.
D.
AD
1、在某行星上用弹簧来秤测量某一物体的重力。在赤道上测量的示数比在两极处测量的示数小1/10,若该行星一昼夜的运行时间为T,万有引力常量为G,则这颗行星的密度为多少?
30π/GT
2
2、如果地球自转加快,地球赤道上物体的重量将发生怎样的变化?
1.4小时
当自转周期等于多少时可使赤道上的物体飘起来?
减小
连续物或卫星群的判断问题
9:根据观察,在土星外层有一个环带,该环带有星云等物质构成,为了判断环带是土星的连续物还是小卫星群。可测出环中各层的线速度v与该层到土星中心的距离R之间的关系,从而加以确定。对此下列判断正确的是:(
)
A.若v与R成正比,则环带是连续物
B.若v与R成正比,则环带是小卫星群
C.若v与R成反比,则环带是连续物
D.若v与R成反比,则环带是小卫星群
AD
12.1990年3月,紫金山天文台将1965年9月20日发现的一颗小行星命名为吴健雄星,直径为32km,如果该行星的密度与地球相同,则对该小行星来说,其上物体的第一宇宙速度约为多少?
(已知地球半径为6400km,地球上第一宇宙速度为7.9km/s)
解:由于"吴健雄星"的密度与地球的密度相近,
所以有M地/(4πr3地/3)=M吴/(4πr3吴/3)
即M吴=M地(r吴/r地)3
代入环绕速度公式得
v=√GM吴/r吴=√GM地r吴2/r地3=r吴v1/r地=20m/s
13.恒星演化发展到一定阶段,可能成为恒星世界的“侏儒”——中子星.中子星的半径较小,一般在7
km—20
km,但它的密度大得惊人.若某中子星的半径为10
km,密度为1.2×1017kg/m3,那么该中子星上的第一宇宙速度约为(
)
A.7.9
km/s
B.16.7
km/s
C.2.9×104
km/s
D.5.8×104
km/s
