人教版数学七年级上册3.4.4 实际问题与一元一次方程---行程问题件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级上册3.4.4 实际问题与一元一次方程---行程问题件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 14:45:58 | ||
图片预览





文档简介
学习目标
理解并掌握行程问题中常见的数量关系.
根据行程问题中的数量关系列一元一次方程解决实际问题,并掌握解此类问题的一般思路.
复习回顾
2.行程问题中常见的量都有什么?
路程=速度×时间 速度=路程时间??????????时间=路程速度
?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
典例解析
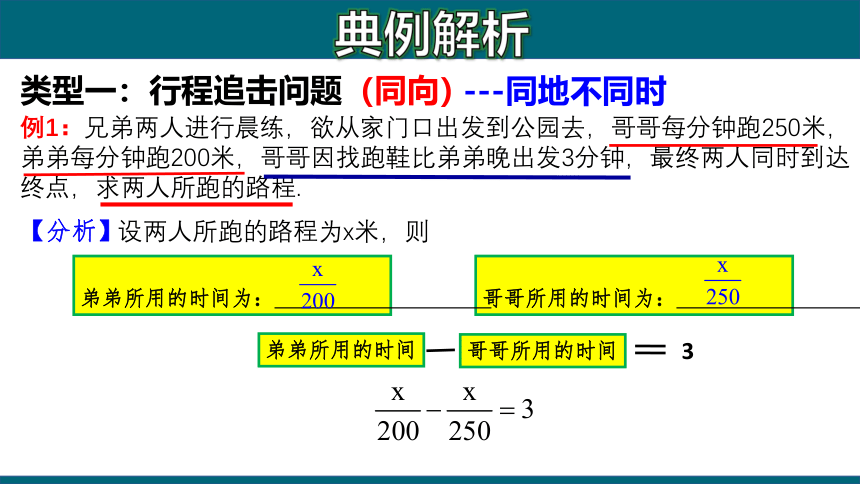
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设两人所跑的路程为x米,则
哥哥所用的时间为:
弟弟所用的时间为:
哥哥所用的时间
弟弟所用的时间
3
【分析】
类型一:行程追击问题(同向)
---同地不同时
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设两人所跑的路程为x米.根据题意列方程,得:
解得: x=3000
答:两人所跑的路程为3000米.
还有别的方法吗?
典例解析
类型一:行程追击问题(同向)
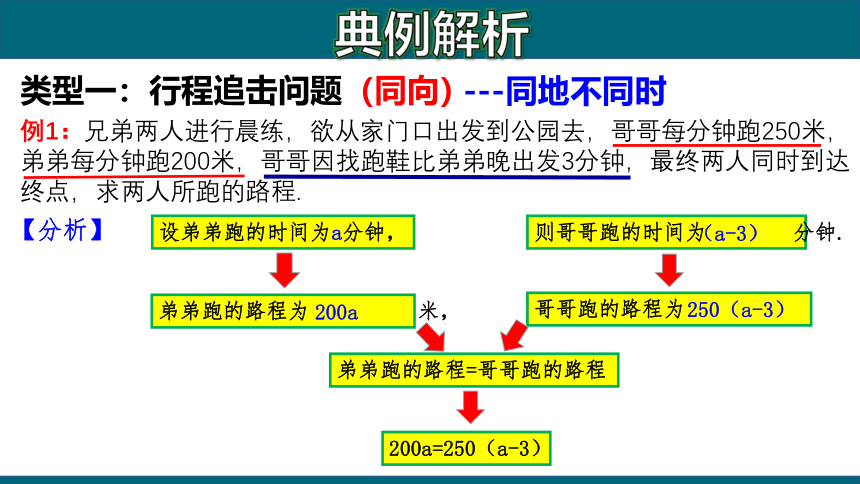
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
---同地不同时
典例解析
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
典例解析
甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙.
针对练习
典例解析
例2:甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
类型二:行程追击问题(同向)
---同时不同地
快
慢
甲站
乙站
450km
慢
快
设x小时快车才能追上慢车,则
65x
85x
【分析】
等量关系:快车路程-慢车路程=路程差
例2:甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
典例解析
典例解析
类型三:行程相遇问题(相向)
---同时出发
例3:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.两车相向而行多少小时相遇?
快
慢
450km
甲站
乙站
65x
85x
【分析】
设x小时两车相遇.
等量关系:快车路程+慢车路程=相距距离
例3:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行使65km;一列快车从乙站开出,每小时行使85km.两车相向而行多少小时相遇?
解:设x小时两车相遇,根据题意列方程,得:
85x+65x=450
解得: x=3
答:两车相向而行3小时相遇.
典例解析
类型四:行程相遇问题(相向)
例4:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
---不同时出发
快
慢
450km
甲站
乙站
65x
85(x+1)
【分析】
慢车行使了x小时两车相遇.
等量关系:快车路程+慢车路程=相距距离
典例解析
典例解析
例4:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
解:慢车行使了x小时两车相遇,根据题意列方程,得:
85(x+1)+65x=450
解得: x=7130
答:慢车行使了7130小时两车相遇.
?
【分析】等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例5 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h.已知水流的速度是 3 km/h,求船在静水中的平均速度.
解:设船在静水中的平均速度为 x km/h,则顺流速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得 2x + 6 = 2.5x-7.5.
移项及合并同类项,得 0.5x = 13.5.
系数化为1,得 x = 27.
答:船在静水中的平均速度为 27 km/h.
根据顺流速度×顺流时间=逆流速度 ×逆流时间,列出方程,得
2( x+3 ) = 2.5( x-3 ).
类型五:顺逆流问题
典例解析
一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
针对练习
例6:运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
【分析】圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
类型六:环形跑道问题
典例解析
例6:运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,根据题意列方程,得:
350x-250x=400
解得: x=4
答:经过4分钟甲、乙相遇.
典例解析
理解并掌握行程问题中常见的数量关系.
根据行程问题中的数量关系列一元一次方程解决实际问题,并掌握解此类问题的一般思路.
复习回顾
2.行程问题中常见的量都有什么?
路程=速度×时间 速度=路程时间??????????时间=路程速度
?
路程 速度 时间
3.行程问题中常见的量之间的数量关系是什么?
1.行程问题常见题型?
相向而行---相遇问题 同向而行---追击问题
典例解析
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设两人所跑的路程为x米,则
哥哥所用的时间为:
弟弟所用的时间为:
哥哥所用的时间
弟弟所用的时间
3
【分析】
类型一:行程追击问题(同向)
---同地不同时
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设两人所跑的路程为x米.根据题意列方程,得:
解得: x=3000
答:两人所跑的路程为3000米.
还有别的方法吗?
典例解析
类型一:行程追击问题(同向)
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
设弟弟跑的时间为a分钟,
则哥哥跑的时间为 分钟.
弟弟跑的路程为 米,
哥哥跑的路程为 米.
弟弟跑的路程=哥哥跑的路程
200a=250(a-3)
【分析】
(a-3)
200a
250(a-3)
---同地不同时
典例解析
例1:兄弟两人进行晨练,欲从家门口出发到公园去,哥哥每分钟跑250米,弟弟每分钟跑200米,哥哥因找跑鞋比弟弟晚出发3分钟,最终两人同时到达终点,求两人所跑的路程.
解:设弟弟跑的时间为a分钟,则哥哥跑的时间为(a-3)分钟.
根据题意列方程,得:
200a=250(a-3)
解得: a=15
所以:15×200=3000(米)
答:两人所跑的路程为3000米.
典例解析
甲、乙两名同学练习百米赛跑,甲每秒跑7米,乙每秒跑6.5米,如果甲让乙先跑1秒,那么甲经过几秒可以追上乙?
解:设甲经过x秒后追上乙,则依题意可得
6.5×(x+1)=7x
解得:x=13
答:甲经过13秒后追上乙.
针对练习
典例解析
例2:甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
类型二:行程追击问题(同向)
---同时不同地
快
慢
甲站
乙站
450km
慢
快
设x小时快车才能追上慢车,则
65x
85x
【分析】
等量关系:快车路程-慢车路程=路程差
例2:甲、乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km,一列快车从乙站开出,每小时行驶85km.问两车同时开出,同向而行,多少小时快车才能追上慢车?
解:设x小时快车才能追上慢车,根据题意列方程,得:
85x-65x=450
解得: x=22.5
答: 22.5小时快车才能追上慢车.
典例解析
典例解析
类型三:行程相遇问题(相向)
---同时出发
例3:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.两车相向而行多少小时相遇?
快
慢
450km
甲站
乙站
65x
85x
【分析】
设x小时两车相遇.
等量关系:快车路程+慢车路程=相距距离
例3:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行使65km;一列快车从乙站开出,每小时行使85km.两车相向而行多少小时相遇?
解:设x小时两车相遇,根据题意列方程,得:
85x+65x=450
解得: x=3
答:两车相向而行3小时相遇.
典例解析
类型四:行程相遇问题(相向)
例4:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
---不同时出发
快
慢
450km
甲站
乙站
65x
85(x+1)
【分析】
慢车行使了x小时两车相遇.
等量关系:快车路程+慢车路程=相距距离
典例解析
典例解析
例4:甲乙两站间的路程为450km,一列慢车从甲站开出,每小时行驶65km;一列快车从乙站开出,每小时行驶85km.快车先开1小时,两车相向而行,慢车行使了多少小时两车相遇?
解:慢车行使了x小时两车相遇,根据题意列方程,得:
85(x+1)+65x=450
解得: x=7130
答:慢车行使了7130小时两车相遇.
?
【分析】等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例5 一艘船从甲码头到乙码头顺流而行,用了 2 h;从乙码头返回甲码头逆流而行,用了 2.5 h.已知水流的速度是 3 km/h,求船在静水中的平均速度.
解:设船在静水中的平均速度为 x km/h,则顺流速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得 2x + 6 = 2.5x-7.5.
移项及合并同类项,得 0.5x = 13.5.
系数化为1,得 x = 27.
答:船在静水中的平均速度为 27 km/h.
根据顺流速度×顺流时间=逆流速度 ×逆流时间,列出方程,得
2( x+3 ) = 2.5( x-3 ).
类型五:顺逆流问题
典例解析
一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24)km/h.
根据题意,得 .
解得 x=840.
两城市的距离为3×(840-24)=2448 (km).
答:两城市之间的距离为2448 km.
针对练习
例6:运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
【分析】圆形跑道中的规律:
快的人跑的路程-慢的人跑的路程=1圈(第1次相遇)
快的人跑的路程-慢的人跑的路程=2圈(第2次相遇)
快的人跑的路程-慢的人跑的路程=3圈(第3次相遇)
……….
类型六:环形跑道问题
典例解析
例6:运动场的跑道一圈长400m,甲练习骑自行车,平均每分骑350m,乙练习跑步,平均每分跑250m.两人从同一处同时同向出发,经过多少时间首次相遇?
解:设经过x分钟首次相遇,根据题意列方程,得:
350x-250x=400
解得: x=4
答:经过4分钟甲、乙相遇.
典例解析
