人教版数学七年级上册4.2.4 线段的和、差、倍、分(二)课件(共18张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.2.4 线段的和、差、倍、分(二)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 00:00:00 | ||
图片预览




文档简介
学习目标
学会利用分类讨论的思想方法求线段的长度.
了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
复习回顾
例 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
【分析】分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
【点睛】无图时求线段的长,应注意分类讨论,一般分以下两种情况:1.点在某一线段上;2.点在该线段的延长线.
典例解析
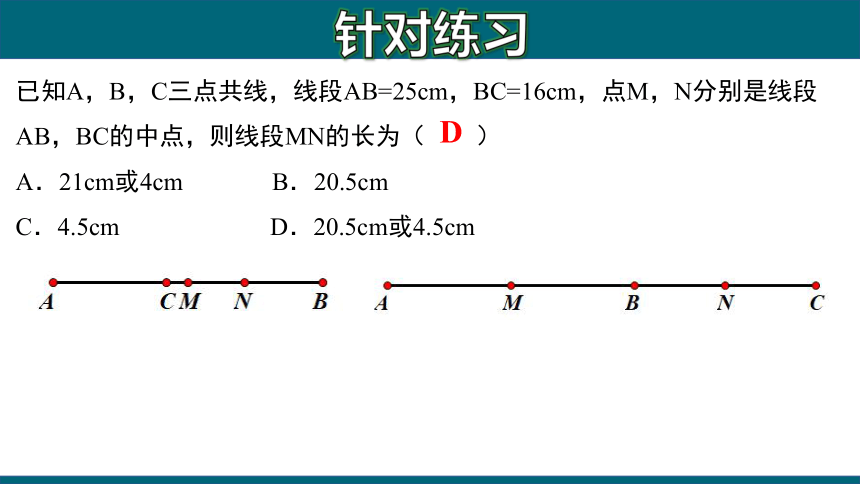
已知A,B,C三点共线,线段AB=25cm,BC=16cm,点M,N分别是线段AB,BC的中点,则线段MN的长为( )
A.21cm或4cm B.20.5cm
C.4.5cm D.20.5cm或4.5cm
D
针对练习
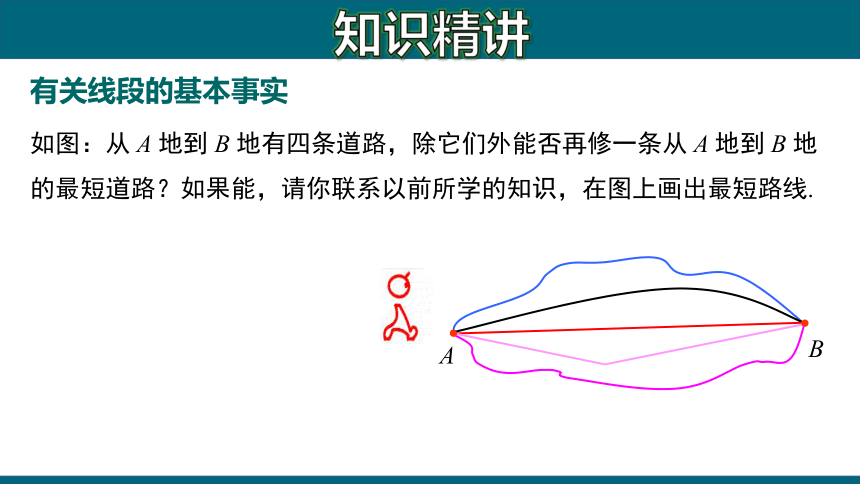
有关线段的基本事实
如图:从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
?
?
A
B
知识精讲
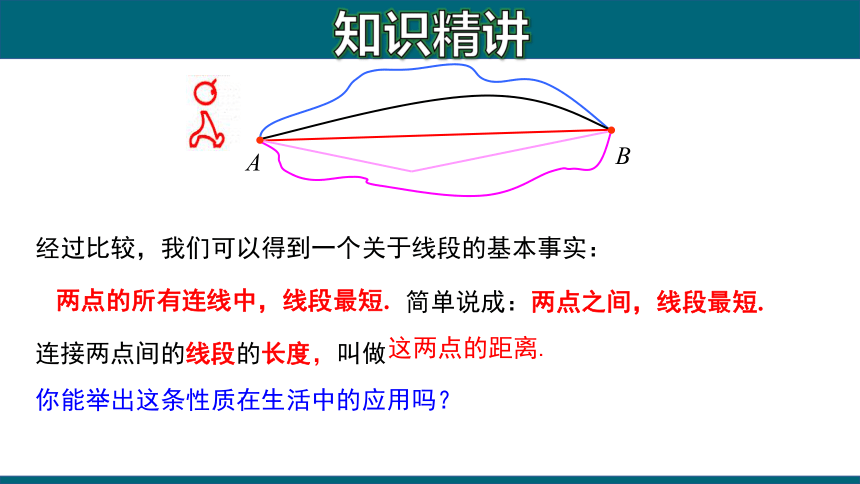
经过比较,我们可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
连接两点间的线段的长度,叫做
这两点的距离.
?
?
A
B
你能举出这条性质在生活中的应用吗?
简单说成:两点之间,线段最短.
知识精讲
两点之间线段最短
1. 如图,这是 A,B 两地之间的公路,在公路工程改造计划时,为使 A,B 两地行程最短,应如何设计线路?请在图中画出,并说明理由.
.
B
A
.
实际应用
2. 把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A
B
A,B 两地间的河道长度变短.
实际应用
3. 如图,AB+BC AC,AC+BC AB,AB+AC BC (填“>”“<”或“=”). 其中蕴含的数学道理是 .
>
两点之间线段最短
>
>
A
B
C
实际应用
4. 在一条笔直的公路两侧,分别有 A,B 两个村庄, 如图,现在要在公路 l 上建一个汽车站 C,使汽车站到 A,B 两村庄的距离之和最小,请在图中画出汽车站的位置.
C
A
B
l
实际应用
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
C
A C D B
AD=BC
达标检测
3.已知线段 AB = 6 cm,延长 AB 到 C,使 BC = 2 AB,若 D 为 AB 的中点,则线段 DC 的长为________.
C
A
D
B
15 cm
4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.
1或9
达标检测
5. 如图,点C 是线段AB 的中点,若 AB = 8 cm,则 AC = cm.
4
C
A
C
B
6. 如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
达标检测
7.如图,AB=20cm,C为AB上的点,且AC=4cm,D是AC的中点,E是BC的中点,求线段DE的长.
解:∵AB=20cm,AC=4cm,
∴CB=AB-AC=20-4=16cm,
又∵D是AC中点,E是BC中点,
∴DC= 12AC= 12?×4=2cm,CE= 12?CB= 12?×18=8cm,
∴DE=DC+CE=2+8=10cm.
?
达标检测
8.已知,如图,B、C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6 cm,求线段MC的长.
解:∵B,C两点把线段AD分成2:4:3三部分,
∴设AB=2x,BC=4x,CD=3x,
∵CD=6cm,即3x=6cm,解得x=2cm,
∴AD=2x+4x+3x=9x=9×2=18cm,
∵M是AD的中点,
∴MD=0.5AD=0.5×18=9cm,
∴MC=MD-CD=9-6=3cm.
达标检测
线段的和差倍分
基本事实
线段的和差
中点
两点间的距离
思想方法
方程思想
分类思想
小结梳理
学会利用分类讨论的思想方法求线段的长度.
了解两点间距离的意义,理解“两点之间,线段最短”的线段性质,并学会运用.
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
复习回顾
例 A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
【分析】分以下两种情况进行讨论:?当点C在AB之间上,故AC=AB-BC=1cm;?当点C在AB的延长线上时,AC=AB+BC=9cm.
C
【点睛】无图时求线段的长,应注意分类讨论,一般分以下两种情况:1.点在某一线段上;2.点在该线段的延长线.
典例解析
已知A,B,C三点共线,线段AB=25cm,BC=16cm,点M,N分别是线段AB,BC的中点,则线段MN的长为( )
A.21cm或4cm B.20.5cm
C.4.5cm D.20.5cm或4.5cm
D
针对练习
有关线段的基本事实
如图:从 A 地到 B 地有四条道路,除它们外能否再修一条从 A 地到 B 地的最短道路?如果能,请你联系以前所学的知识,在图上画出最短路线.
?
?
A
B
知识精讲
经过比较,我们可以得到一个关于线段的基本事实:
两点的所有连线中,线段最短.
连接两点间的线段的长度,叫做
这两点的距离.
?
?
A
B
你能举出这条性质在生活中的应用吗?
简单说成:两点之间,线段最短.
知识精讲
两点之间线段最短
1. 如图,这是 A,B 两地之间的公路,在公路工程改造计划时,为使 A,B 两地行程最短,应如何设计线路?请在图中画出,并说明理由.
.
B
A
.
实际应用
2. 把原来弯曲的河道改直,A,B 两地间的河道长度有什么变化?
A
B
A,B 两地间的河道长度变短.
实际应用
3. 如图,AB+BC AC,AC+BC AB,AB+AC BC (填“>”“<”或“=”). 其中蕴含的数学道理是 .
>
两点之间线段最短
>
>
A
B
C
实际应用
4. 在一条笔直的公路两侧,分别有 A,B 两个村庄, 如图,现在要在公路 l 上建一个汽车站 C,使汽车站到 A,B 两村庄的距离之和最小,请在图中画出汽车站的位置.
C
A
B
l
实际应用
1. 下列说法正确的是 ( )
A. 两点间距离的定义是指两点之间的线段
B. 两点之间的距离是指两点之间的直线
C. 两点之间的距离是指连接两点之间线段的长度
D. 两点之间的距离是两点之间的直线的长度
2. 如图,AC = DB,则图中另外两条相等的线段为_____________.
C
A C D B
AD=BC
达标检测
3.已知线段 AB = 6 cm,延长 AB 到 C,使 BC = 2 AB,若 D 为 AB 的中点,则线段 DC 的长为________.
C
A
D
B
15 cm
4.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若BC=5,则AC=_________.
1或9
达标检测
5. 如图,点C 是线段AB 的中点,若 AB = 8 cm,则 AC = cm.
4
C
A
C
B
6. 如图,下列说法,不能判断点C 是线段AB 的中点的是 ( )
A. AC = CB B. AB = 2 AC
C. AC + CB = AB D. CB = AB
A
C
B
达标检测
7.如图,AB=20cm,C为AB上的点,且AC=4cm,D是AC的中点,E是BC的中点,求线段DE的长.
解:∵AB=20cm,AC=4cm,
∴CB=AB-AC=20-4=16cm,
又∵D是AC中点,E是BC中点,
∴DC= 12AC= 12?×4=2cm,CE= 12?CB= 12?×18=8cm,
∴DE=DC+CE=2+8=10cm.
?
达标检测
8.已知,如图,B、C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6 cm,求线段MC的长.
解:∵B,C两点把线段AD分成2:4:3三部分,
∴设AB=2x,BC=4x,CD=3x,
∵CD=6cm,即3x=6cm,解得x=2cm,
∴AD=2x+4x+3x=9x=9×2=18cm,
∵M是AD的中点,
∴MD=0.5AD=0.5×18=9cm,
∴MC=MD-CD=9-6=3cm.
达标检测
线段的和差倍分
基本事实
线段的和差
中点
两点间的距离
思想方法
方程思想
分类思想
小结梳理
