人教版数学七年级上册4.3.2 角的平分线及相关运算课件(共16张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.2 角的平分线及相关运算课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 15:13:25 | ||
图片预览




文档简介
学习目标
理解角平分线的意义及数量关系,能够用几何语言进行相关表述.
灵活利用角平分线与角的和、差、倍、分的数量关系,解答相关问题.
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
复习回顾
B
A
O
C
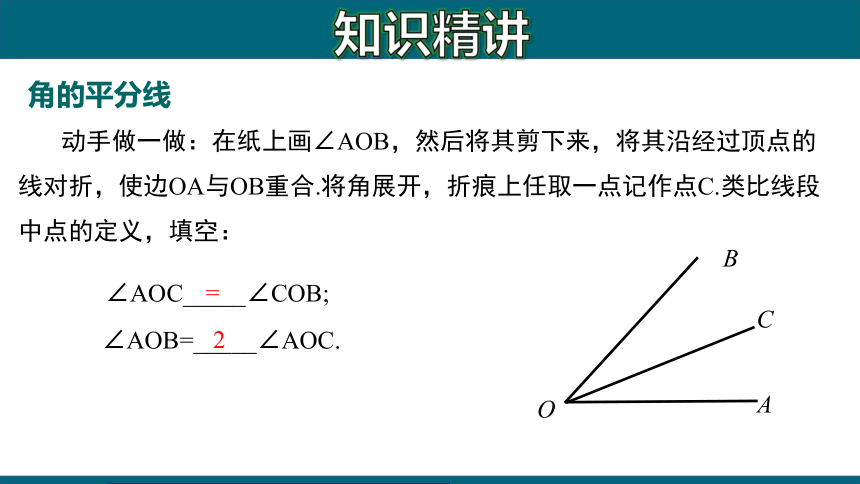
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
角的平分线
知识精讲
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
角的平分线
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
知识精讲
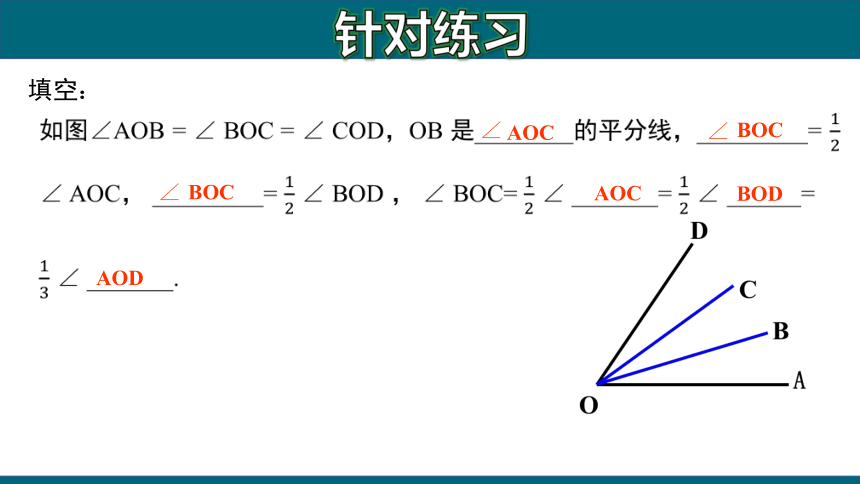
如图∠AOB = ∠ BOC = ∠ COD,OB 是________的平分线,_________= 12 ∠ AOC, _________= 12 ∠ BOD , ∠ BOC= 12 ∠ _______= 12 ∠ ______=
13 ∠ _______.
?
AOC
BOC
BOC
AOC
填空:
BOD
AOD
针对练习
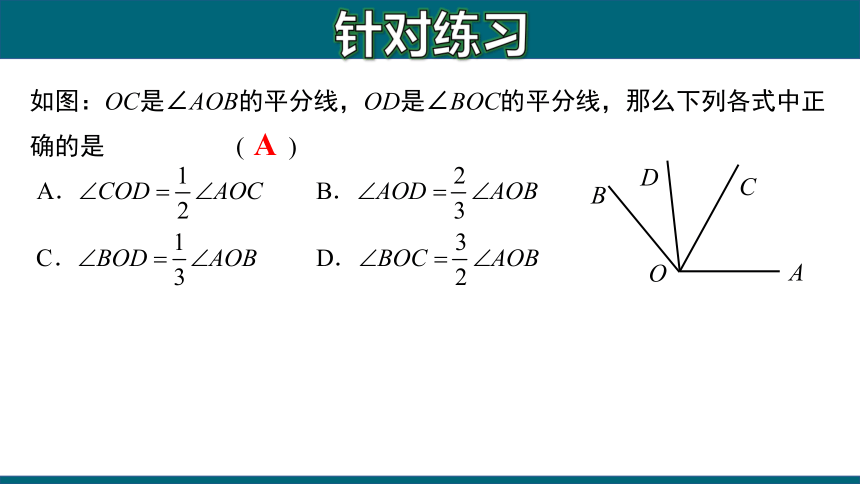
如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
针对练习
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以∠BOC= ∠AOC= ×80°=40°.
典例解析
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
O
A
B
C
D
E
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
典例解析
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
解:因为 ∠COD=30°, OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC= ×80°= 40°.
典例解析
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.
求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°
∴∠AOC=2x=2×8°=16°
∵OD平分∠AOB,
∴∠AOD=20°
∴∠COD=∠AOD-∠AOC=20°-16°=4°
C
D
?如图,OC在∠AOB内部,OD平分∠AOB,
典例解析
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.
求OC与∠AOB的平分线所成的角的度数.
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
?如图,OC在∠AOB外部,OD平分∠AOB,
∴OC与∠AOB的平分线所成的角的度数为4°或100°.
【点睛】涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
典例解析
如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
针对练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
针对练习
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
角的平分线
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
思想方法
方程思想
分类思想
小结梳理
理解角平分线的意义及数量关系,能够用几何语言进行相关表述.
灵活利用角平分线与角的和、差、倍、分的数量关系,解答相关问题.
A
a
a
M
B
M 是线段 AB 的中点
几何语言:∵ M 是线段 AB 的中点
∴ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
反之也成立:∵ AM = MB = AB
( 或 AB = 2 AM = 2 MB )
∴ M 是线段 AB 的中点
说明:在几何中我们可以把
因为用“∵”表示;所以用“∴”表示.
复习回顾
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
角的平分线
知识精讲
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
角的平分线
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
知识精讲
如图∠AOB = ∠ BOC = ∠ COD,OB 是________的平分线,_________= 12 ∠ AOC, _________= 12 ∠ BOD , ∠ BOC= 12 ∠ _______= 12 ∠ ______=
13 ∠ _______.
?
AOC
BOC
BOC
AOC
填空:
BOD
AOD
针对练习
如图:OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是 ( )
A
O
A
B
C
D
针对练习
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
(1) 如果∠AOC=80°,那么∠BOC 是多少度?
解:因为 OB 平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以∠BOC= ∠AOC= ×80°=40°.
典例解析
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
O
A
B
C
D
E
(2) 如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
解:因为 OB 平分∠AOC,
所以 ∠BOC=∠AOB = 40°.
因为 OD 平分∠COE,
所以∠COD=∠DOE = 30°,
所以∠BOD =∠BOC+∠COD = 40°+30°= 70°.
典例解析
例1 如图,OB 是∠AOC 的平分线,OD 是∠COE的平分线.
O
A
B
C
D
E
(3) 如果∠AOE=140°, ∠COD=30°,那么∠AOB是多少度?
解:因为 ∠COD=30°, OD 平分∠COE,
所以 ∠COE=2∠COD=60°,
所以 ∠AOC=∠AOE-∠COE
=140°-60°= 80°.
又因为 OB 平分∠AOC,
所以∠AOB= ∠AOC= ×80°= 40°.
典例解析
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.
求OC与∠AOB的平分线所成的角的度数.
O
A
B
解:分以下两种情况:
设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,∴2x+3x=40°,得x=8°
∴∠AOC=2x=2×8°=16°
∵OD平分∠AOB,
∴∠AOD=20°
∴∠COD=∠AOD-∠AOC=20°-16°=4°
C
D
?如图,OC在∠AOB内部,OD平分∠AOB,
典例解析
例2 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3.
求OC与∠AOB的平分线所成的角的度数.
∴设∠AOC=2x,∠COB=3x,
∵∠AOB=40°,
∴3x-2x=40°,得x=40°,
∴∠AOC=2x=2×40°=80°,
∵OD平分∠AOB,∴∠AOD=20°,
∴∠COD=∠AOC+∠AOD=80°+20°=100°.
O
A
B
C
D
?如图,OC在∠AOB外部,OD平分∠AOB,
∴OC与∠AOB的平分线所成的角的度数为4°或100°.
【点睛】涉及到角度的计算时,除常规的和差倍分计算外,通常还需运用方程思想和分类讨论思想解决问题.
典例解析
如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
(1) 求∠EOD的度数;
解:∵∠AOB=120°,
OD平分∠BOC,
OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC
= (∠BOC+∠AOC )
= ∠AOB= ×120°=60°.
针对练习
(2) 若∠BOC=90°,求∠AOE的度数.
解:∵∠AOB=120°,
∠BOC=90°,
∴∠AOC=120°-90°
=30°.
∵OE平分∠AOC,
∴∠AOE= ∠AOC= ×30°=15°.
如图,∠AOB=120°,OD平分∠BOC,OE平分∠AOC.
针对练习
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
O
B
A
C
角的平分线
∵ OC 是∠AOB 的角平分线,
∴ ∠AOC =∠BOC = ∠AOB,
∠AOB =2∠BOC =2∠AOC.
思想方法
方程思想
分类思想
小结梳理
