人教版数学七年级上册4.3.2 角的度量与单位换算课件(共15张PPT)
文档属性
| 名称 | 人教版数学七年级上册4.3.2 角的度量与单位换算课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 15:25:42 | ||
图片预览



文档简介
学习目标
认识角的单位,会进行度、分、秒之间的换算.
会正确使用量角器测量角的大小.
角的有关概念
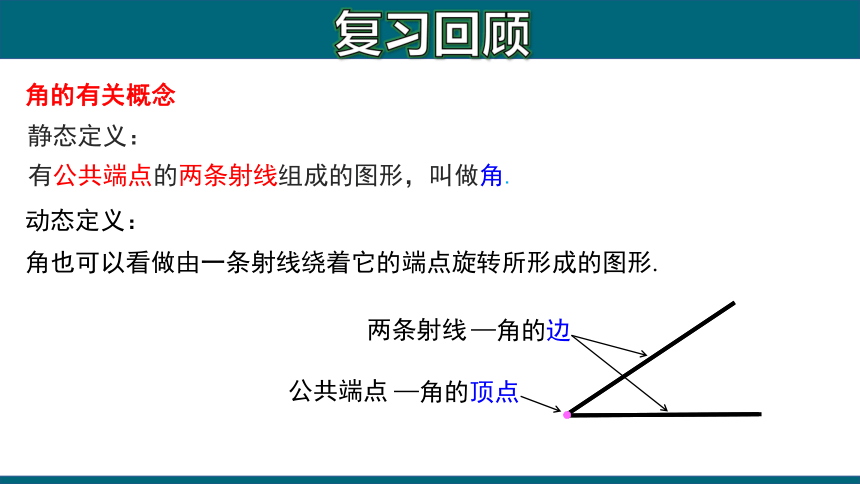
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
动态定义:
角也可以看做由一条射线绕着它的端点旋转所形成的图形.
复习回顾
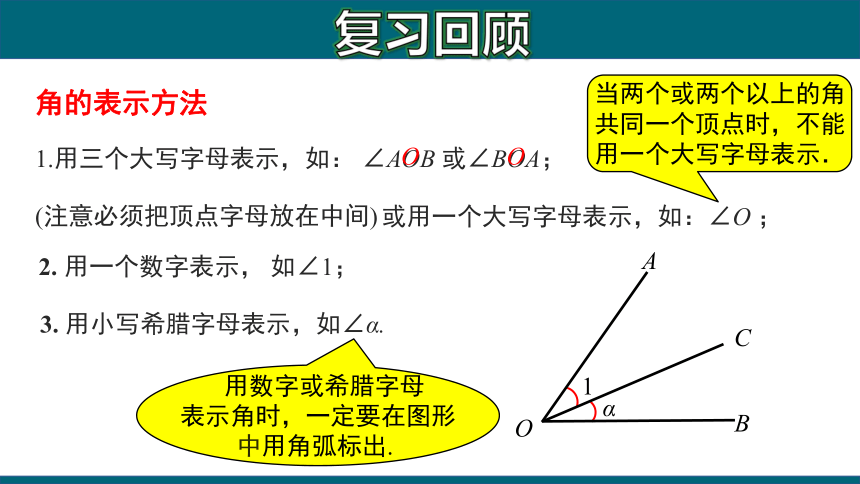
(注意必须把顶点字母放在中间)
1.用三个大写字母表示,如: ∠AOB 或∠BOA;
或用一个大写字母表示,如:∠O ;
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
O O
角的表示方法
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母
表示角时,一定要在图形
中用角弧标出.
复习回顾
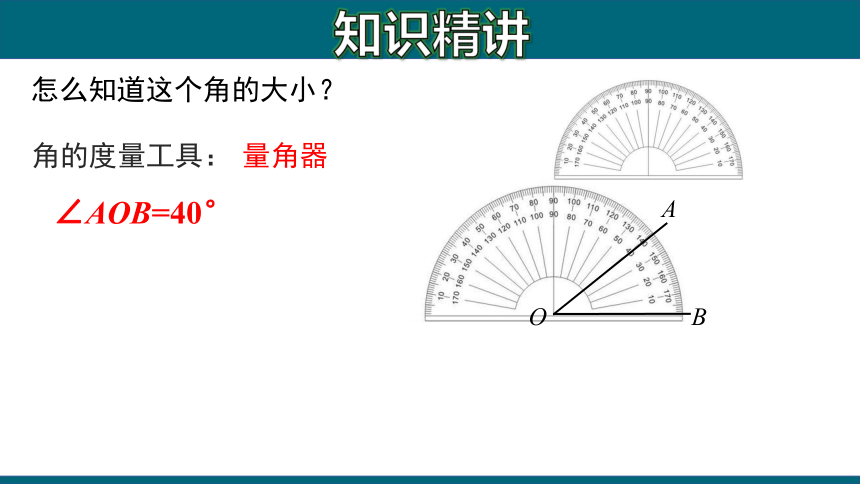
角的度量工具:
量角器
怎么知道这个角的大小?
A
B
O
∠AOB=40°
知识精讲
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分.
每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
知识精讲
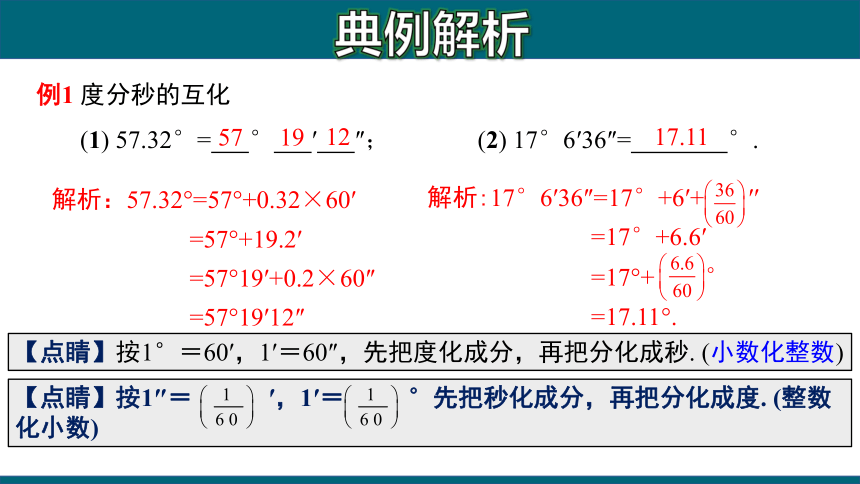
例1 度分秒的互化
(1) 57.32°= ° ′ ″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
【点睛】按1°=60′,1′=60″,先把度化成分,再把分化成秒. (小数化整数)
57
19
12
(2) 17°6′36″= °.
17.11
解析:17°6′36″=17°+6′+ ′′
=17°+6.6′
=17?+ °
=17.11?.
【点睛】按1″= ′,1′= °先把秒化成分,再把分化成度. (整数化小数)
典例解析
300
18000
38
9
0.6
0.01
38.25
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
度分秒的互化
针对练习
例2 如图,时钟显示为10:10时,时针与分针所夹角度是 ( )
A.90° B.100° C.105° D.115°
【分析】时针每小时旋转的夹角360°÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
典例解析
1.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲:“3时整和3时30分”
B.乙说“6时15分和6时45分”
C.丙说“9时整和12时15分”
D.丁说:“3时整和9时整”
D
针对练习
1.用度、分、秒表示91.34°为( )
A.91°20′24″ B.91°34′ C.91°20′4″ D.91°3′4″
A
2.下列各式成立的是 ( )
A.62.5°=62°50′ B.31°12′36″=31.21°
C.106°18′18″=106.33° D.62°24′=62.24°
B
达标检测
(1)把周角平均分成360份,每份就是____的角,1°=____ ′ ,1′=_____″;
(2)25.72°=____ °____ ′ _____″;
(3)15°48′36"=______ °;
(4)624"=______ ′.
3.填空:
达标检测
1°
60
60
25
43
12
15.81
10.4
4. 38°15′和38.15°相等吗?如不相等,请说明它们的大小关系.
解:∵ 38°15′ = 38.25°,
∴ 38°15′ > 38.15°.
你还有别的方法吗?
达标检测
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分.
每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
小结梳理
认识角的单位,会进行度、分、秒之间的换算.
会正确使用量角器测量角的大小.
角的有关概念
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
动态定义:
角也可以看做由一条射线绕着它的端点旋转所形成的图形.
复习回顾
(注意必须把顶点字母放在中间)
1.用三个大写字母表示,如: ∠AOB 或∠BOA;
或用一个大写字母表示,如:∠O ;
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示.
O O
角的表示方法
2. 用一个数字表示, 如∠1;
3. 用小写希腊字母表示,如∠α.
α
1
A
B
O
C
用数字或希腊字母
表示角时,一定要在图形
中用角弧标出.
复习回顾
角的度量工具:
量角器
怎么知道这个角的大小?
A
B
O
∠AOB=40°
知识精讲
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分.
每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
知识精讲
例1 度分秒的互化
(1) 57.32°= ° ′ ″;
解析:57.32?=57?+0.32×60′
=57?+19.2′
=57?19′+0.2×60″
=57?19′12″
【点睛】按1°=60′,1′=60″,先把度化成分,再把分化成秒. (小数化整数)
57
19
12
(2) 17°6′36″= °.
17.11
解析:17°6′36″=17°+6′+ ′′
=17°+6.6′
=17?+ °
=17.11?.
【点睛】按1″= ′,1′= °先把秒化成分,再把分化成度. (整数化小数)
典例解析
300
18000
38
9
0.6
0.01
38.25
5°= ′= ″;38.15°= ° ′;36″= ′= °;
38°15′= °.
度分秒的互化
针对练习
例2 如图,时钟显示为10:10时,时针与分针所夹角度是 ( )
A.90° B.100° C.105° D.115°
【分析】时针每小时旋转的夹角360°÷12=30°,故10分钟,时针旋转的角度为5°,即10:10时,时针与分针所夹角度为4×30°-5°=115°.
D
典例解析
1.甲、乙、丙、丁,四名学生在判断钟表的分针和时针互相垂直的时刻时,每人说了两个时刻,说法都对的是( )
A.甲:“3时整和3时30分”
B.乙说“6时15分和6时45分”
C.丙说“9时整和12时15分”
D.丁说:“3时整和9时整”
D
针对练习
1.用度、分、秒表示91.34°为( )
A.91°20′24″ B.91°34′ C.91°20′4″ D.91°3′4″
A
2.下列各式成立的是 ( )
A.62.5°=62°50′ B.31°12′36″=31.21°
C.106°18′18″=106.33° D.62°24′=62.24°
B
达标检测
(1)把周角平均分成360份,每份就是____的角,1°=____ ′ ,1′=_____″;
(2)25.72°=____ °____ ′ _____″;
(3)15°48′36"=______ °;
(4)624"=______ ′.
3.填空:
达标检测
1°
60
60
25
43
12
15.81
10.4
4. 38°15′和38.15°相等吗?如不相等,请说明它们的大小关系.
解:∵ 38°15′ = 38.25°,
∴ 38°15′ > 38.15°.
你还有别的方法吗?
达标检测
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角 360等分.
每一份就是 1 度的角,记作1°;
把 1 度的角 60 等分,每一份叫做1 分的角,记作 1′;把1分的角 60等分,每一份叫做1 秒的角,记作1″.
1周角= °;1平角= °.
360
180
1°= ′;1′= ″.
60
60
小结梳理
