人教版数学八年级上册15.3.2 分式方程的解的情况专题课课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册15.3.2 分式方程的解的情况专题课课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 17:32:36 | ||
图片预览






文档简介
学习目标
理解分式方程可能无解的原因.
能解决根据分式方程根的情况,确定字母的值或取值范围.
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去。
4.写出原方程的根.
简记为:“一化二解三检验”.
“去分母法”解分式方程的步骤
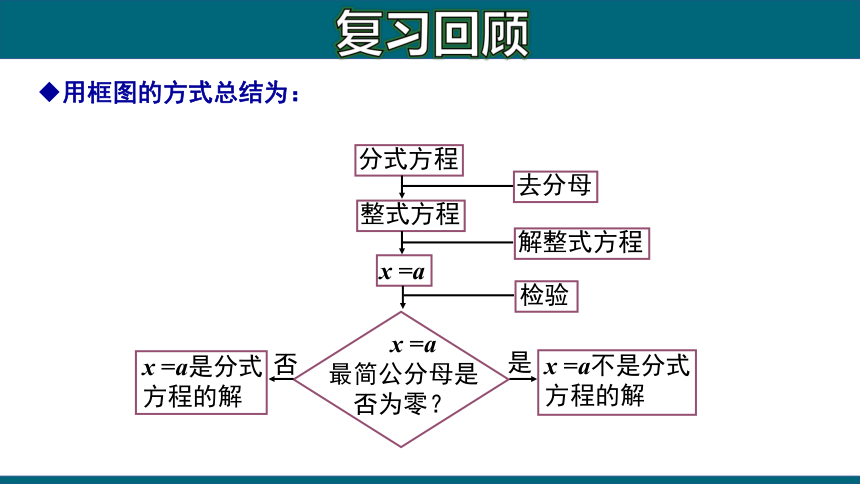
复习回顾
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
否
是
复习回顾
解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
复习回顾
例1
关于x的方程 的解是正数,则a的取值范围是____________.
解析:去分母得2x+a=x-1,解得x=-a-1,
∵关于x的方程 的解是正数,
∴x>0且x≠1,
∴-a-1>0且-a-1≠1,
解得a<-1且a≠-2,
∴a的取值范围是a<-1且a≠-2.
【点睛】求出方程的解(用未知字母表示),然后根据解的正负性,列关于未知字母的不等式求解,特别注意分母不能为0.
a<-1且a≠-2
典例解析
若关于x的分式方程 有非负数解,则a的取值范围是_______.
解:分式方程去分母得:2x=3a-4(x-1),
移项合并得:6x=3a+4,
解得:x=3????+46,
∵分式方程的解为非负数,
∴ 3????+46?≥0且3????+46?-1≠0,
解得:a≥-43且a≠23.
?
针对练习
解:去分母,得-3(x+1)+a(x-1)=8,
∵原方程有增根,
∴最简公分母(1-x)(x+1)=0,
解得x=1或-1,
当x=1时,-6=8,这是不可能的.
当x=-1时,-2a=8,此时a=-4.
由此可得方程的增根为-1.
若 有增根,则这个方程的增根是_______.
例2
典例解析
若关于x的方程 有增根,则m的值是_______.
解:方程两边都乘以(x-2)得,
2-x-m=2(x-2),
∵分式方程有增根,
∴x-2=0,
解得x=2,
∴2-2-m=2(2-2),
解得m=0.
针对练习
若关于x的分式方程 无解,求m的值.
例3
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
解:方程两边都乘以(x+2)(x-2)得2(x+2)+mx=3(x-2),
即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10得(m-1)×2=-10,m=-4;
当x=-2时,代入(m-1)x=-10得(m-1)×(-2)=-10,解得m=6,
∴m的值是1,-4或6.
典例解析
已知关于x的方程 无解,求m的值.
解:去分母,整理得
(m+3)x=4m+8,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即m+3=0,
而4m+8≠0,此时m=-3.
(2)方程①的根是增根,增根是x=3,把x=3代入方程①解得m=1.
因此,m的值为-3或1.
针对练习
方法总结:分式方程无解与分式方程有增根所表达的意义是不一样的.
分式方程有增根仅仅针对使最简公分母为0的数,分式方程无解不但包括使最简公分母为0的数,而且还包括分式方程化为整式方程后,使整式方程无解的数.
归纳总结
D
2. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
1.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
达标检测
3. 解分式方程 时,去分母后得到的整式方程是( )
A.2(x-8)+5x=16(x-7) B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7) D.2(x-8)-5x=8
A
4.若关于x的分式方程 无解,则m的值为 ( )
A.-1,5 B.1
C.-1.5或2 D.-0.5或-1.5
D
达标检测
5.已知关于x的分式方程 的解是非负数,则m的取值范围是( )
A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠3
C
6.若分式方程 有增根,则k=_______.
解:去分母得:2(x-2)+1-kx=-1,
整理得:(2-k)x=2,
∵分式方程有增根,
∴x-2=0,2-x=0,
解得:x=2,
把x=2代入(2-k)x=2得:k=1.
达标检测
理解分式方程可能无解的原因.
能解决根据分式方程根的情况,确定字母的值或取值范围.
1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去。
4.写出原方程的根.
简记为:“一化二解三检验”.
“去分母法”解分式方程的步骤
复习回顾
用框图的方式总结为:
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
否
是
复习回顾
解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
复习回顾
例1
关于x的方程 的解是正数,则a的取值范围是____________.
解析:去分母得2x+a=x-1,解得x=-a-1,
∵关于x的方程 的解是正数,
∴x>0且x≠1,
∴-a-1>0且-a-1≠1,
解得a<-1且a≠-2,
∴a的取值范围是a<-1且a≠-2.
【点睛】求出方程的解(用未知字母表示),然后根据解的正负性,列关于未知字母的不等式求解,特别注意分母不能为0.
a<-1且a≠-2
典例解析
若关于x的分式方程 有非负数解,则a的取值范围是_______.
解:分式方程去分母得:2x=3a-4(x-1),
移项合并得:6x=3a+4,
解得:x=3????+46,
∵分式方程的解为非负数,
∴ 3????+46?≥0且3????+46?-1≠0,
解得:a≥-43且a≠23.
?
针对练习
解:去分母,得-3(x+1)+a(x-1)=8,
∵原方程有增根,
∴最简公分母(1-x)(x+1)=0,
解得x=1或-1,
当x=1时,-6=8,这是不可能的.
当x=-1时,-2a=8,此时a=-4.
由此可得方程的增根为-1.
若 有增根,则这个方程的增根是_______.
例2
典例解析
若关于x的方程 有增根,则m的值是_______.
解:方程两边都乘以(x-2)得,
2-x-m=2(x-2),
∵分式方程有增根,
∴x-2=0,
解得x=2,
∴2-2-m=2(2-2),
解得m=0.
针对练习
若关于x的分式方程 无解,求m的值.
例3
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
解:方程两边都乘以(x+2)(x-2)得2(x+2)+mx=3(x-2),
即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10得(m-1)×2=-10,m=-4;
当x=-2时,代入(m-1)x=-10得(m-1)×(-2)=-10,解得m=6,
∴m的值是1,-4或6.
典例解析
已知关于x的方程 无解,求m的值.
解:去分母,整理得
(m+3)x=4m+8,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即m+3=0,
而4m+8≠0,此时m=-3.
(2)方程①的根是增根,增根是x=3,把x=3代入方程①解得m=1.
因此,m的值为-3或1.
针对练习
方法总结:分式方程无解与分式方程有增根所表达的意义是不一样的.
分式方程有增根仅仅针对使最简公分母为0的数,分式方程无解不但包括使最简公分母为0的数,而且还包括分式方程化为整式方程后,使整式方程无解的数.
归纳总结
D
2. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
1.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
达标检测
3. 解分式方程 时,去分母后得到的整式方程是( )
A.2(x-8)+5x=16(x-7) B.2(x-8)+5x=8
C.2(x-8)-5x=16(x-7) D.2(x-8)-5x=8
A
4.若关于x的分式方程 无解,则m的值为 ( )
A.-1,5 B.1
C.-1.5或2 D.-0.5或-1.5
D
达标检测
5.已知关于x的分式方程 的解是非负数,则m的取值范围是( )
A.m>2 B.m≥2 C.m≥2且m≠3 D.m>2且m≠3
C
6.若分式方程 有增根,则k=_______.
解:去分母得:2(x-2)+1-kx=-1,
整理得:(2-k)x=2,
∵分式方程有增根,
∴x-2=0,2-x=0,
解得:x=2,
把x=2代入(2-k)x=2得:k=1.
达标检测
