人教版数学八年级上册15.3.3 分式方程的应用(一)--工程问题课件(共15张PPT)
文档属性
| 名称 | 人教版数学八年级上册15.3.3 分式方程的应用(一)--工程问题课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 00:00:00 | ||
图片预览





文档简介
学习目标
在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.
理解工程问题数量关系正确列出分式方程.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
复习回顾
4.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有3种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)工程问题: 工作量=工时×工效以及它的两个变式;
(3)利润问题: 批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价.
复习回顾
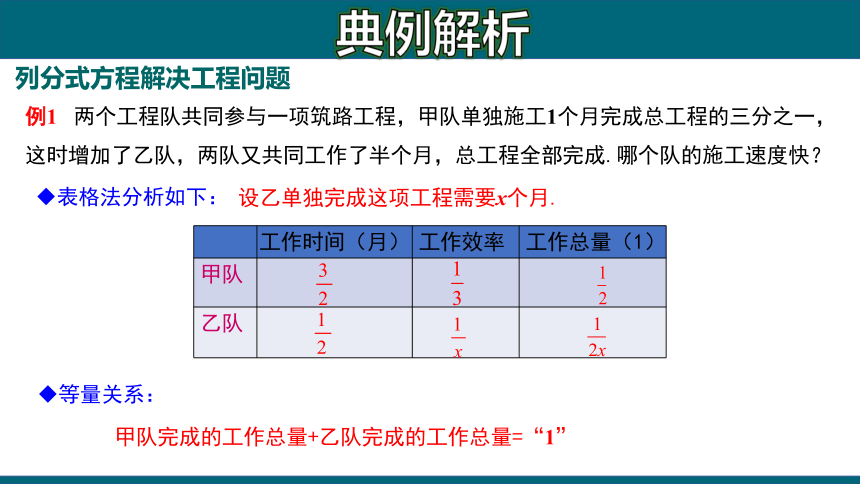
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工作时间(月)
工作效率
工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
列分式方程解决工程问题
典例解析
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
典例解析
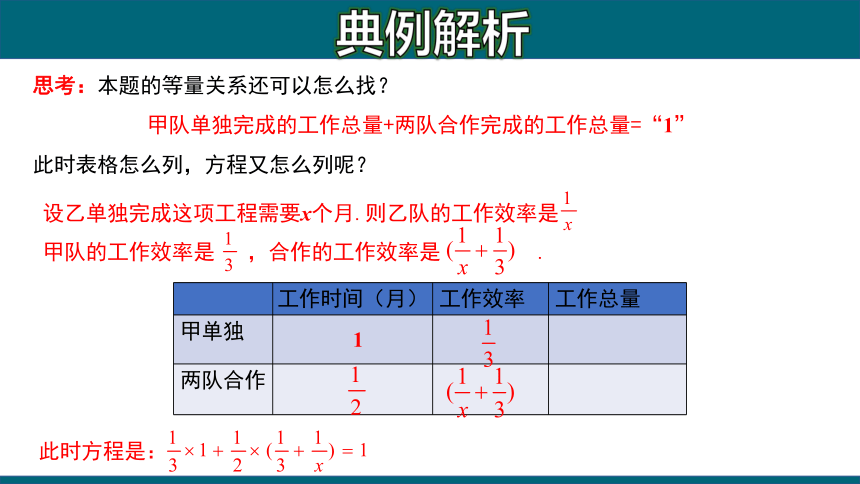
思考:本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
此时表格怎么列,方程又怎么列呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工作时间(月)
工作效率
工作总量
甲单独
两队合作
设乙单独完成这项工程需要x个月.则乙队的工作效率是 甲队的工作效率是 ,合作的工作效率是 .
此时方程是:
1
典例解析
工程问题
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如× ×单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2指该类问题中的“两个主人公”如甲队和乙队,或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
归纳总结
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.写:答案.
归纳总结
抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
解析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
针对练习
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时.
由题意得 .
解得x=6.
经检验x=6是方程的解.∴x+3=9.
答:甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
针对练习
1.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产x台机器,则可列方程为( )
A. B. C. D.
C
2.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为( )
A. B.
C. D.
B
达标检测
3.某厂一个车间计划在一定时间内加工560个零件,在加工120个零件后,改进了操作技术,每天能多加工15个零件,结果比原计划提前3天完成任务.求改进操作技术后每天加工的零件个数.
解:设改进操作技术后每天加工x个零件,则原来每天加工(x-15)个零件,根据题意列方程得,
即:x2-15x-2200=0.
解得:x1=55,x2=-40(舍去).
答:改进技术后每天加工55个.
达标检测
小结梳理
在不同的实际问题中能审明题意设未知数,列分式方程解决实际问题.
理解工程问题数量关系正确列出分式方程.
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.通常使用第一种方法.
复习回顾
4.我们现在所学过的应用题有哪几种类型?每种类型的基本公式是什么?
基本上有3种:
(1)行程问题: 路程=速度×时间以及它的两个变式;
(2)工程问题: 工作量=工时×工效以及它的两个变式;
(3)利润问题: 批发成本=批发数量×批发价;批发数量=批发成本÷批发价;打折销售价=定价×折数;销售利润=销售收入一批发成本;每本销售利润=定价一批发价;每本打折销售利润=打折销售价一批发价,利润率=利润÷进价.
复习回顾
例1 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队的施工速度快?
表格法分析如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工作时间(月)
工作效率
工作总量(1)
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
列分式方程解决工程问题
典例解析
解:设乙单独完成这项工程需要x个月.记工作总量为1,甲的工作效率是 ,根据题意得
即
方程两边都乘以2x,得
解得 x=1.
检验:当x=1时,6x≠0.
所以,原分式方程的解为x=1.
由上可知,若乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,所以乙队的施工速度快.
典例解析
思考:本题的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
此时表格怎么列,方程又怎么列呢?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
工作时间(月)
工作效率
工作总量
甲单独
两队合作
设乙单独完成这项工程需要x个月.则乙队的工作效率是 甲队的工作效率是 ,合作的工作效率是 .
此时方程是:
1
典例解析
工程问题
1.题中有“单独”字眼通常可知工作效率;
2.通常间接设元,如× ×单独完成需 x(单位时间),则可表示出其工作效率;
4.解题方法:可概括为“321”,即3指该类问题中三量关系,如工程问题有工作效率,工作时间,工作量;2指该类问题中的“两个主人公”如甲队和乙队,或“甲单独和两队合作”;1指该问题中的一个等量关系.如工程问题中等量关系是:两个主人公工作总量之和=全部工作总量.
3.弄清基本的数量关系.如本题中的“合作的工效=甲乙两队工作效率的和”.
归纳总结
列分式方程解应用题的一般步骤
1.审:清题意,并设未知数;
2.找:相等关系;
3.列:出方程;
4.解:这个分式方程;
5.验:根(包括两方面 :(1)是否是分式方程的根; (2)是否符合题意);
6.写:答案.
归纳总结
抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
解析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
针对练习
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时.
由题意得 .
解得x=6.
经检验x=6是方程的解.∴x+3=9.
答:甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
针对练习
1.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产x台机器,则可列方程为( )
A. B. C. D.
C
2.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为( )
A. B.
C. D.
B
达标检测
3.某厂一个车间计划在一定时间内加工560个零件,在加工120个零件后,改进了操作技术,每天能多加工15个零件,结果比原计划提前3天完成任务.求改进操作技术后每天加工的零件个数.
解:设改进操作技术后每天加工x个零件,则原来每天加工(x-15)个零件,根据题意列方程得,
即:x2-15x-2200=0.
解得:x1=55,x2=-40(舍去).
答:改进技术后每天加工55个.
达标检测
小结梳理
