人教版数学八年级上册第15章 分式章节复习课件(共37张PPT)
文档属性
| 名称 | 人教版数学八年级上册第15章 分式章节复习课件(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 14:26:34 | ||
图片预览











文档简介
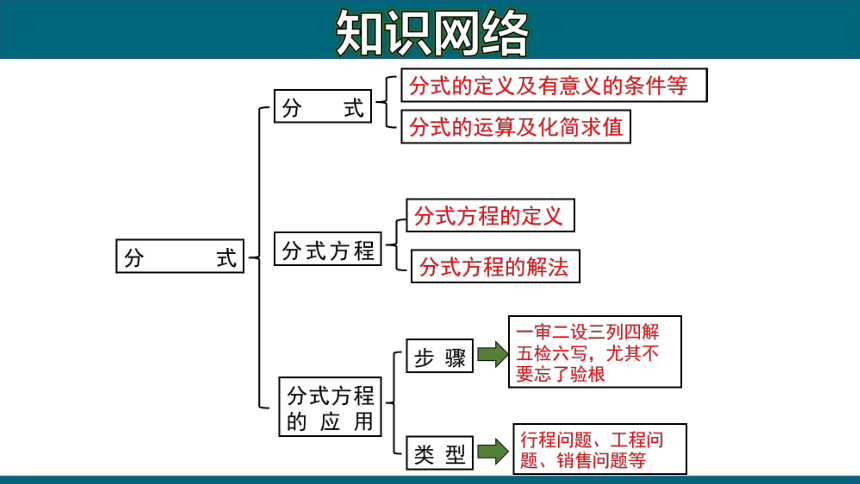
知识网络
一、分式
1.分式的概念:
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B为分式的分母.
2.分式有意义的条件:
对于分式 :
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
知识梳理
3.分式值为零的条件:
当___________时,分式 的值为零.
A=0且 B≠0
4.分式的基本性质:
知识梳理
5.分式的约分:
约分的定义
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式的定义
分子与分母没有公因式的式子,叫做最简分式
注意:分式的约分,一般要约去分子和分母所有的公因式,使所得的结果成为最简分式或整式.
知识梳理
约分的基本步骤
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
知识梳理
6.分式的通分:
分式的通分的定义
根据分式的基本性质,使分子、分母同乘适当的整式(即最简公分母),把分母不相同的分式变成分母相同的分式,这种变形叫分式的通分.
最简公分母
为通分先要确定各分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,叫做最简公分母.
知识梳理
二、分式的运算
1.分式的乘除法则:
2.分式的乘方法则:
知识梳理
3.分式的加减法则:
(1)同分母分式的加减法则:
(2)异分母分式的加减法则:
知识梳理
4.分式的混合运算:
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
知识梳理
三、分式方程
1.分式方程的定义
分母中含未知数的方程叫做分式方程.
2.分式方程的解法
(1)在方程的两边都乘以最简公分母,约去分母,化成整式方程.
(2)解这个整式方程.
(3)把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去.
知识梳理
3.分式方程的应用
列分式方程解应用题的一般步骤
(1)审:清题意,并设未知数;
(2)找:相等关系;
(3)列:出方程;
(4)解:这个分式方程;
(5)验:根(包括两方面 :?是否是分式方程的根; ?是否符合题意);
(5)写:答案.
知识梳理
【例1】 如果分式 的值为0,那么x的值为 .
考点解析
分式的有关概念
1
【解析】 如果分式的值为0,则分子等于0且分母不为0.
解:根据分式的值为0可得:
X2-1=0且x+1≠0
解得:x=1.
【点睛】分式有意义的条件是分母不为0,分式无意义的条件是分母的值为0;分式的值为0的条件是:分子为0而分母不为0.
1
2.如果分式 的值为零,则a的值为 .
1.若分式 无意义,则a的值 .
迁移应用
【解析】 如果分式无意义,则分母等于0.
-3
2
解:根据分式的值为0可得:
????-2=0且a+2≠0
解得:a=2.
?
【例2】如果把分式 中的x和y的值都扩大为原来的3倍,则分式的值( )
A.扩大为原来的3倍 B.不变
C.缩小为原来的 D.缩小为原来的
考点解析
分式的性质及有关计算
2
B
【解析】 因为????????????????+????????=????????????(????+????)=????????+????,所以把分式中的x和y的值都扩大为原来的3倍,分式的值不变.
?
3.下列变形正确的是( )
迁移应用
C
【例3】已知x= ,y= ,求 值.
【解析】本题中给出字母的具体取值,因此要先化简分式再代入求值.
考点解析
解原式=
当x=1-2,y=1+2时,原式=
?
【点睛】对于一个分式,如果给出其中字母的取值,我们可以先将分式进行化简,再把字母取值代入,即可求出分式的值.但对于某些分式的求值问题,却没有直接给出字母的取值,而只是给出字母满足的条件,这样的问题较复杂,需要根据具体情况选择适当的方法.
4.先化简,再求值: 再从-4<x<4的范围内选取一个合适的整数x代入求值.
解析:先计算括号里的减法运算,再把除法运算转化成乘法运算,进行约分化简,最后从x的取值范围内选取一数值代入即可.
迁移应用
【点睛】把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
迁移应用
【例4】
考点解析
解析:由已知发现a与1????互为倒数,可以得到a2+1????2的值,对所要求的代数式分子分母同时除以a2,然后整体代入即可求出答案.
?
解:由已知可得:a2+1????2=(????+1????)2?2=25-2=23.
对代数式分子分母同时除以a2,得:
1????2+1+1????2=123+1=124
?
【点睛】利用x和1????互为倒数的关系,沟通已知条件与所求未知代数式的关系,可以使一些分式求值问题的思路豁然开朗,使解题过程简洁.
?
5.已知x2-5x+1=0,求出 的值.
迁移应用
解:对已知进行变形,等号两边同时除以x可得:x+1????=5.
根据完全平方公式变形,得:
?
【例5】解方程
解: 方程两边乘x(x-3),得
2x=3x-9.
解得
x=9.
检验:当x=9时,x(x-3) ≠0.
所以,原分式方程的解为x=9.
分式方程的解法
3
解: 方程两边乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3.
解得
x=1.
检验:当x=1时, (x-1)(x+2) =0, 因此x=1不是原分式方程的解.
所以,原分式方程无解.
考点解析
【点睛】解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.
D
7. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
6.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
迁移应用
8.解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
迁移应用
根据分式方程的解的情况求参数
4
考点解析
【例6】
关于x的方程 的解是正数,则a的取值范围是____________.
解析:去分母得2x+a=x-1,解得x=-a-1,
∵关于x的方程 的解是正数,
∴x>0且x≠1,
∴-a-1>0且-a-1≠1,
解得a<-1且a≠-2,
∴a的取值范围是a<-1且a≠-2.
【点睛】求出方程的解(用未知字母表示),然后根据解的正负性,列关于未知字母的不等式求解,特别注意分母不能为0.
a<-1且a≠-2
迁移应用
9.若关于x的分式方程 有非负数解,则a的取值范围是_______.
解:分式方程去分母得:2x=3a-4(x-1),
移项合并得:6x=3a+4,
解得:x=3????+46,
∵分式方程的解为非负数,
∴ 3????+46?≥0且3????+46?-1≠0,
解得:a≥-43且a≠23.
?
解:去分母,得-3(x+1)+a(x-1)=8,
∵原方程有增根,
∴最简公分母(1-x)(x+1)=0,
解得x=1或-1,
当x=1时,-6=8,这是不可能的.
当x=-1时,-2a=8,此时a=-4.
由此可得方程的增根为-1.
若 有增根,则这个方程的增根是_______.
【例7】
考点解析
10.若关于x的方程 有增根,则m的值是_______.
解:方程两边都乘以(x-2)得,
2-x-m=2(x-2),
∵分式方程有增根,
∴x-2=0,
解得x=2,
∴2-2-m=2(2-2),
解得m=0.
迁移应用
若关于x的分式方程 无解,求m的值.
【例8】
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
解:方程两边都乘以(x+2)(x-2)得2(x+2)+mx=3(x-2),
即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10得(m-1)×2=-10,m=-4;
当x=-2时,代入(m-1)x=-10得(m-1)×(-2)=-10,解得m=6,
∴m的值是1,-4或6.
考点解析
11.已知关于x的方程 无解,求m的值.
解:去分母,整理得
(m+3)x=4m+8,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即m+3=0,
而4m+8≠0,此时m=-3.
(2)方程①的根是增根,增根是x=3,把x=3代入方程①解得m=1.
因此,m的值为-3或1.
迁移应用
【例9】从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
解析:(1)根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍,两数相乘即可;
分式方程的应用
5
考点解析
解:
400×1.3=520(千米)
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
解析:设普通列车的平均速度是x千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可.
考点解析
解:设普通列车的平均速度是x千米/时,那么高铁的平均速度2.5x千米/时,依题意得:
解得
x=120.
经检验,x=120是原方程的根.
由x=120得2.5x=300.
答:高铁的平均速度300千米/时.
12.农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的根.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
迁移应用
【例10】抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
解析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
考点解析
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时.
由题意得 .
解得x=6.
经检验x=6是方程的解.∴x+3=9.
答:甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
考点解析
13.某厂一个车间计划在一定时间内加工560个零件,在加工120个零件后,改进了操作技术,每天能多加工15个零件,结果比原计划提前3天完成任务.求改进操作技术后每天加工的零件个数.
解:设改进操作技术后每天加工x个零件,则原来每天加工(x-15)个零件,根据题意列方程得,
即:x2-15x-2200=0.
解得:x1=55,x2=-40(舍去).
答:改进技术后每天加工55个.
迁移应用
一、分式
1.分式的概念:
一般地,如果A、B都表示整式,且B中含有字母,那么称 为分式.其中A叫做分式的分子,B为分式的分母.
2.分式有意义的条件:
对于分式 :
当_______时分式有意义;
当_______时无意义.
B≠0
B=0
知识梳理
3.分式值为零的条件:
当___________时,分式 的值为零.
A=0且 B≠0
4.分式的基本性质:
知识梳理
5.分式的约分:
约分的定义
根据分式的基本性质,把一个分式的分子与分母的公因式约去,叫做分式的约分.
最简分式的定义
分子与分母没有公因式的式子,叫做最简分式
注意:分式的约分,一般要约去分子和分母所有的公因式,使所得的结果成为最简分式或整式.
知识梳理
约分的基本步骤
(1)若分子﹑分母都是单项式,则约去系数的最大公约数,并约去相同字母的最低次幂;
(2)若分子﹑分母含有多项式,则先将多项式分解因式,然后约去分子﹑分母所有的公因式.
知识梳理
6.分式的通分:
分式的通分的定义
根据分式的基本性质,使分子、分母同乘适当的整式(即最简公分母),把分母不相同的分式变成分母相同的分式,这种变形叫分式的通分.
最简公分母
为通分先要确定各分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,叫做最简公分母.
知识梳理
二、分式的运算
1.分式的乘除法则:
2.分式的乘方法则:
知识梳理
3.分式的加减法则:
(1)同分母分式的加减法则:
(2)异分母分式的加减法则:
知识梳理
4.分式的混合运算:
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
计算结果要化为最简分式或整式.
知识梳理
三、分式方程
1.分式方程的定义
分母中含未知数的方程叫做分式方程.
2.分式方程的解法
(1)在方程的两边都乘以最简公分母,约去分母,化成整式方程.
(2)解这个整式方程.
(3)把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则须舍去.
知识梳理
3.分式方程的应用
列分式方程解应用题的一般步骤
(1)审:清题意,并设未知数;
(2)找:相等关系;
(3)列:出方程;
(4)解:这个分式方程;
(5)验:根(包括两方面 :?是否是分式方程的根; ?是否符合题意);
(5)写:答案.
知识梳理
【例1】 如果分式 的值为0,那么x的值为 .
考点解析
分式的有关概念
1
【解析】 如果分式的值为0,则分子等于0且分母不为0.
解:根据分式的值为0可得:
X2-1=0且x+1≠0
解得:x=1.
【点睛】分式有意义的条件是分母不为0,分式无意义的条件是分母的值为0;分式的值为0的条件是:分子为0而分母不为0.
1
2.如果分式 的值为零,则a的值为 .
1.若分式 无意义,则a的值 .
迁移应用
【解析】 如果分式无意义,则分母等于0.
-3
2
解:根据分式的值为0可得:
????-2=0且a+2≠0
解得:a=2.
?
【例2】如果把分式 中的x和y的值都扩大为原来的3倍,则分式的值( )
A.扩大为原来的3倍 B.不变
C.缩小为原来的 D.缩小为原来的
考点解析
分式的性质及有关计算
2
B
【解析】 因为????????????????+????????=????????????(????+????)=????????+????,所以把分式中的x和y的值都扩大为原来的3倍,分式的值不变.
?
3.下列变形正确的是( )
迁移应用
C
【例3】已知x= ,y= ,求 值.
【解析】本题中给出字母的具体取值,因此要先化简分式再代入求值.
考点解析
解原式=
当x=1-2,y=1+2时,原式=
?
【点睛】对于一个分式,如果给出其中字母的取值,我们可以先将分式进行化简,再把字母取值代入,即可求出分式的值.但对于某些分式的求值问题,却没有直接给出字母的取值,而只是给出字母满足的条件,这样的问题较复杂,需要根据具体情况选择适当的方法.
4.先化简,再求值: 再从-4<x<4的范围内选取一个合适的整数x代入求值.
解析:先计算括号里的减法运算,再把除法运算转化成乘法运算,进行约分化简,最后从x的取值范围内选取一数值代入即可.
迁移应用
【点睛】把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分母不能为0.
迁移应用
【例4】
考点解析
解析:由已知发现a与1????互为倒数,可以得到a2+1????2的值,对所要求的代数式分子分母同时除以a2,然后整体代入即可求出答案.
?
解:由已知可得:a2+1????2=(????+1????)2?2=25-2=23.
对代数式分子分母同时除以a2,得:
1????2+1+1????2=123+1=124
?
【点睛】利用x和1????互为倒数的关系,沟通已知条件与所求未知代数式的关系,可以使一些分式求值问题的思路豁然开朗,使解题过程简洁.
?
5.已知x2-5x+1=0,求出 的值.
迁移应用
解:对已知进行变形,等号两边同时除以x可得:x+1????=5.
根据完全平方公式变形,得:
?
【例5】解方程
解: 方程两边乘x(x-3),得
2x=3x-9.
解得
x=9.
检验:当x=9时,x(x-3) ≠0.
所以,原分式方程的解为x=9.
分式方程的解法
3
解: 方程两边乘(x-1)(x+2),得
x(x+2)-(x-1)(x+2)=3.
解得
x=1.
检验:当x=1时, (x-1)(x+2) =0, 因此x=1不是原分式方程的解.
所以,原分式方程无解.
考点解析
【点睛】解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.
D
7. 要把方程 化为整式方程,方程两边可以同乘以( )
A. 3y-6 B. 3y
C. 3 (3y-6) D. 3y (y-2)
6.下列关于x的方程中,是分式方程的是( )
A. B.
C. D.
D
迁移应用
8.解方程:
解:去分母,得
解得
检验:把 代入
所以原方程的解为
迁移应用
根据分式方程的解的情况求参数
4
考点解析
【例6】
关于x的方程 的解是正数,则a的取值范围是____________.
解析:去分母得2x+a=x-1,解得x=-a-1,
∵关于x的方程 的解是正数,
∴x>0且x≠1,
∴-a-1>0且-a-1≠1,
解得a<-1且a≠-2,
∴a的取值范围是a<-1且a≠-2.
【点睛】求出方程的解(用未知字母表示),然后根据解的正负性,列关于未知字母的不等式求解,特别注意分母不能为0.
a<-1且a≠-2
迁移应用
9.若关于x的分式方程 有非负数解,则a的取值范围是_______.
解:分式方程去分母得:2x=3a-4(x-1),
移项合并得:6x=3a+4,
解得:x=3????+46,
∵分式方程的解为非负数,
∴ 3????+46?≥0且3????+46?-1≠0,
解得:a≥-43且a≠23.
?
解:去分母,得-3(x+1)+a(x-1)=8,
∵原方程有增根,
∴最简公分母(1-x)(x+1)=0,
解得x=1或-1,
当x=1时,-6=8,这是不可能的.
当x=-1时,-2a=8,此时a=-4.
由此可得方程的增根为-1.
若 有增根,则这个方程的增根是_______.
【例7】
考点解析
10.若关于x的方程 有增根,则m的值是_______.
解:方程两边都乘以(x-2)得,
2-x-m=2(x-2),
∵分式方程有增根,
∴x-2=0,
解得x=2,
∴2-2-m=2(2-2),
解得m=0.
迁移应用
若关于x的分式方程 无解,求m的值.
【例8】
解析:先把分式方程化为整式方程,再分两种情况讨论求解:一元一次方程无解与分式方程有增根.
解:方程两边都乘以(x+2)(x-2)得2(x+2)+mx=3(x-2),
即(m-1)x=-10.
①当m-1=0时,此方程无解,此时m=1;
②方程有增根,则x=2或x=-2,
当x=2时,代入(m-1)x=-10得(m-1)×2=-10,m=-4;
当x=-2时,代入(m-1)x=-10得(m-1)×(-2)=-10,解得m=6,
∴m的值是1,-4或6.
考点解析
11.已知关于x的方程 无解,求m的值.
解:去分母,整理得
(m+3)x=4m+8,①
由于原方程无解,故有以下两种情况:
(1)方程①无实数根,即m+3=0,
而4m+8≠0,此时m=-3.
(2)方程①的根是增根,增根是x=3,把x=3代入方程①解得m=1.
因此,m的值为-3或1.
迁移应用
【例9】从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
解析:(1)根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍,两数相乘即可;
分式方程的应用
5
考点解析
解:
400×1.3=520(千米)
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
解析:设普通列车的平均速度是x千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可.
考点解析
解:设普通列车的平均速度是x千米/时,那么高铁的平均速度2.5x千米/时,依题意得:
解得
x=120.
经检验,x=120是原方程的根.
由x=120得2.5x=300.
答:高铁的平均速度300千米/时.
12.农机厂到距工厂15千米的向阳村检修农机,一部分人骑自行车先走,过了40分钟,其余人乘汽车去,结果他们同时到达,已知汽车的速度是自行车的3倍,求两车的速度.
解:设自行车的速度为x千米/时,那么汽车的速度是3x千米/时,依题意得:
解得
x=15.
经检验,x=15是原方程的根.
由x=15得3x=45.
答:自行车的速度是15千米/时,汽车的速度是45千米/时.
迁移应用
【例10】抗洪抢险时,需要在一定时间内筑起拦洪大坝,甲队单独做正好按期完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲、乙两队合作2个小时后,甲队又有新任务,余下的由乙队单独做,刚好按期完成.求甲、乙两队单独完成全部工程各需多少小时?
解析:设甲队单独完成需要x小时,则乙队需要(x+3)小时,根据等量关系“甲工效×2+乙工效×甲队单独完成需要时间=1”列方程.
考点解析
解:设甲队单独完成需要x小时,则乙队需要(x+3)小时.
由题意得 .
解得x=6.
经检验x=6是方程的解.∴x+3=9.
答:甲单独完成全部工程需6小时,乙单独完成全部工程需9小时.
解决工程问题的思路方法:各部分工作量之和等于1,常从工作量和工作时间上考虑相等关系.
考点解析
13.某厂一个车间计划在一定时间内加工560个零件,在加工120个零件后,改进了操作技术,每天能多加工15个零件,结果比原计划提前3天完成任务.求改进操作技术后每天加工的零件个数.
解:设改进操作技术后每天加工x个零件,则原来每天加工(x-15)个零件,根据题意列方程得,
即:x2-15x-2200=0.
解得:x1=55,x2=-40(舍去).
答:改进技术后每天加工55个.
迁移应用
