2020-2021学年冀教版数学九年级上册 第26章 解直角三角形 易错题汇编(附解析)
文档属性
| 名称 | 2020-2021学年冀教版数学九年级上册 第26章 解直角三角形 易错题汇编(附解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 534.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第26章
解直角三角形
易错题汇编
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,AB=4,AC=1,那么∠B的余弦值为( )
A.
B.
C.
D.
2.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35°
B.mcos35°
C.
D.
4.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m
B.50m
C.50m
D.m
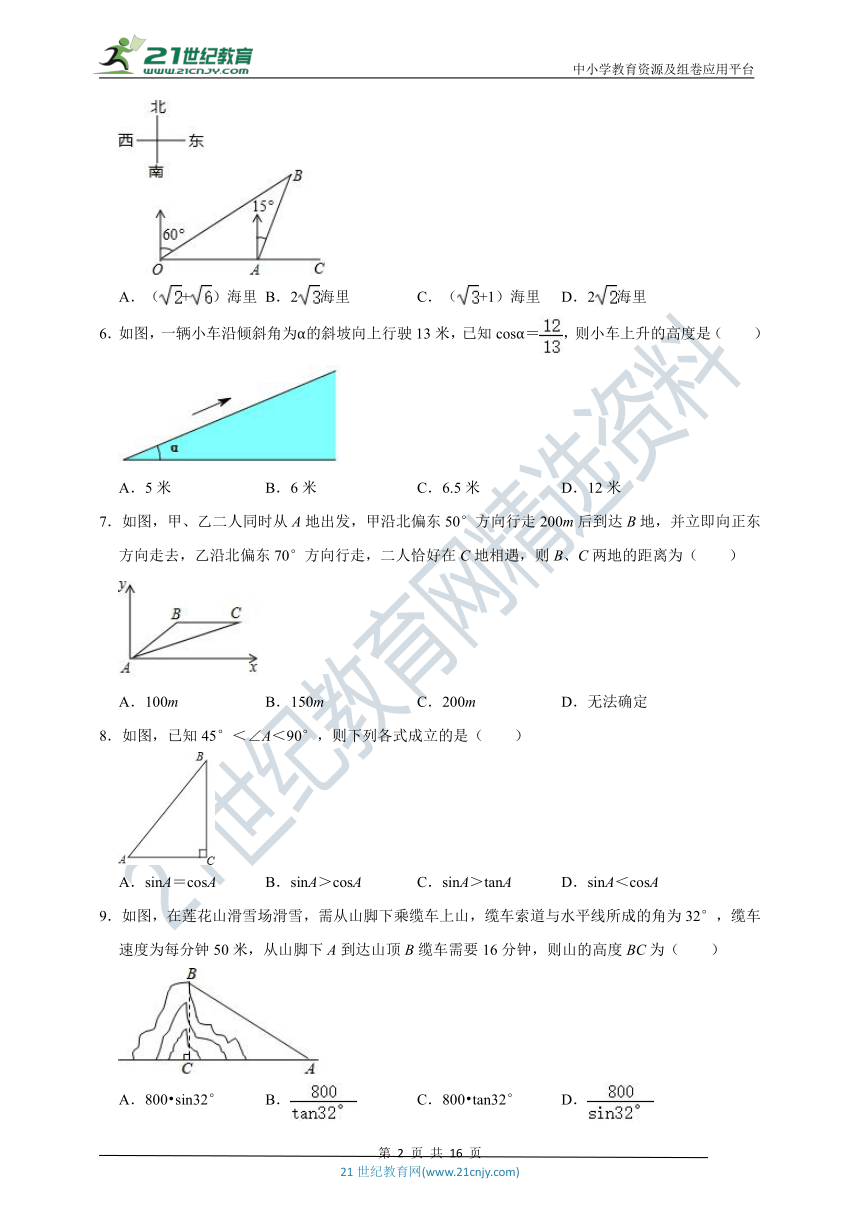
5.如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A.(+)海里
B.2海里
C.(+1)海里
D.2海里
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是( )
A.5米
B.6米
C.6.5米
D.12米
7.如图,甲、乙二人同时从A地出发,甲沿北偏东50°方向行走200m后到达B地,并立即向正东方向走去,乙沿北偏东70°方向行走,二人恰好在C地相遇,则B、C两地的距离为( )
A.100m
B.150m
C.200m
D.无法确定
8.如图,已知45°<∠A<90°,则下列各式成立的是( )
A.sinA=cosA
B.sinA>cosA
C.sinA>tanA
D.sinA<cosA
9.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为( )
A.800?sin32°
B.
C.800?tan32°
D.
10.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米
B.10米
C.20米
D.米
二.填空题(共6小题)
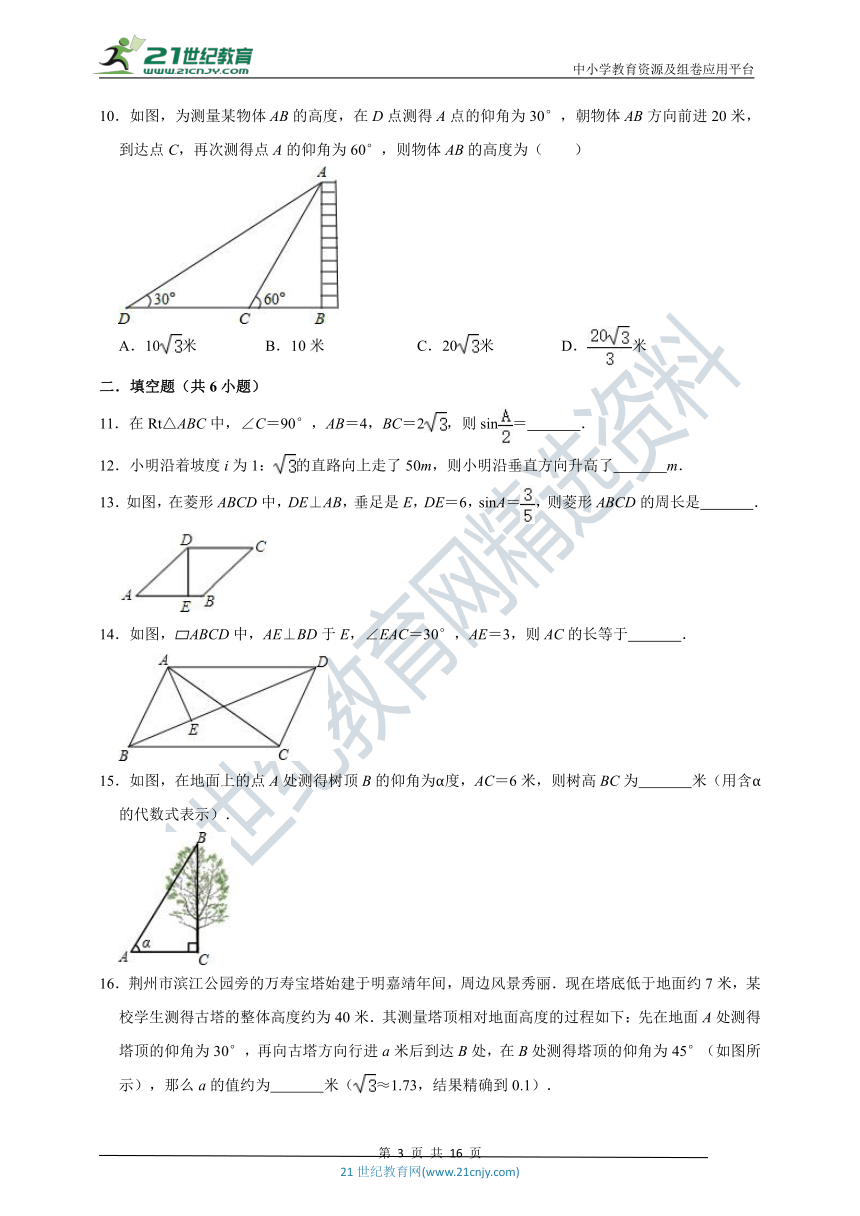
11.在Rt△ABC中,∠C=90°,AB=4,BC=2,则sin=
.
12.小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了
m.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是
.
14.如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于
.
15.如图,在地面上的点A处测得树顶B的仰角为α度,AC=6米,则树高BC为
米(用含α的代数式表示).
16.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为
米(≈1.73,结果精确到0.1).
三.解答题(共4小题)
17.计算题“
(1);
(2).
18.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
(1)若AD=10,sin∠ADC=,求AC的长和tanB的值;
(2)如图,若∠B=a,AD=BD=1,则可以利用该图求出sin2a与a的三角函数之间的等量关系(用sina和cosa的值表示).
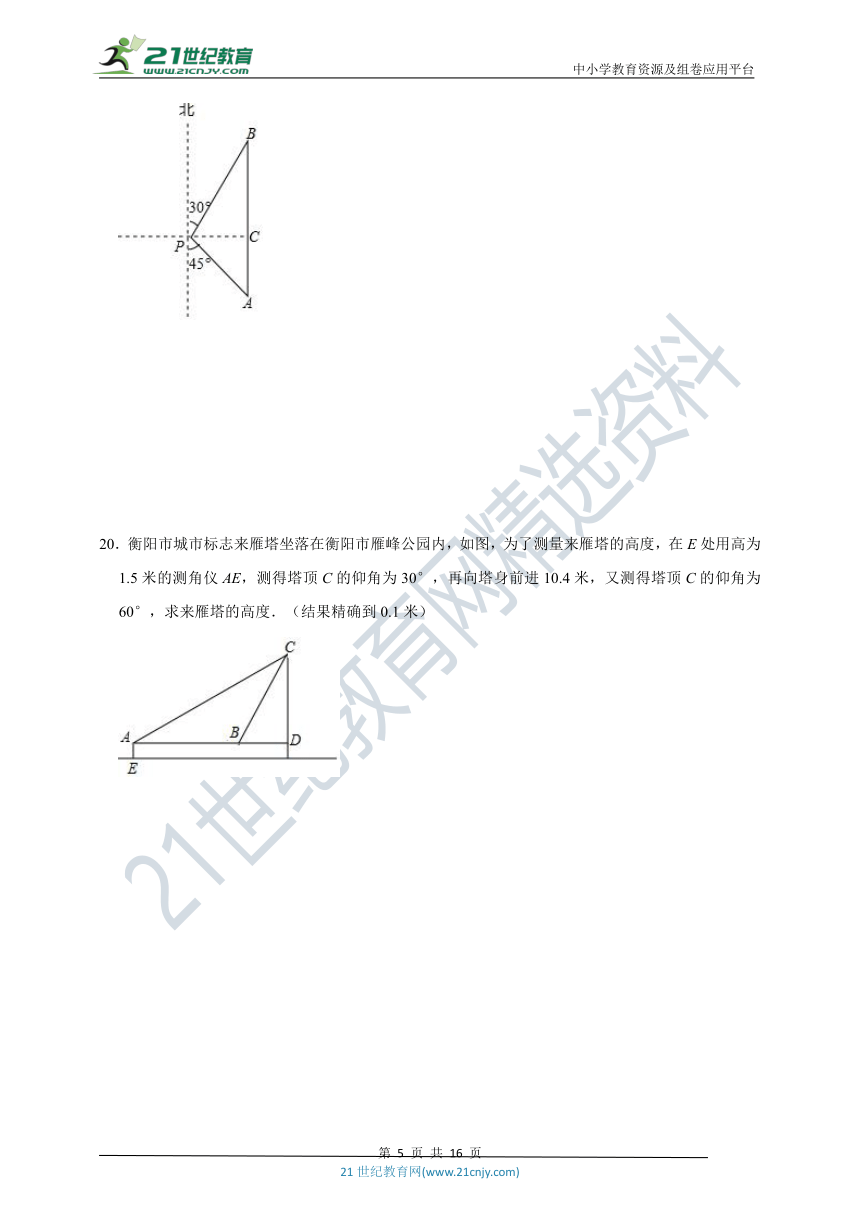
19.随着航母编队的成立,我国海军日益强大.2018年4月12日,中央军委在南海海域隆重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:≈1.414,≈1.732,结果精确到1海里).
20.衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
试题解析
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,AB=4,AC=1,那么∠B的余弦值为( )
A.
B.
C.
D.
解;由勾股定理得BC===,
cos∠B==,
故选:A.
2.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
解:由tan∠B=,得
AC=BC?tanB=5×tan26.
故选:D.
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35°
B.mcos35°
C.
D.
解:sin∠A=,
∵AB=m,∠A=35°,
∴BC=msin35°,
故选:A.
4.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m
B.50m
C.50m
D.m
解:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC===100(m).
故选:A.
5.如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A.(+)海里
B.2海里
C.(+1)海里
D.2海里
解:如图,作BD⊥OC于D,则船A离灯塔B的最近距离是BD的长.作AE⊥OB于E.
在直角△ABE中,∵∠AEB=90°,∠ABE=∠BAD﹣∠AOB=75°﹣30°=45°,AB=4,
∴AE=BE=AB=2.
在直角△AOE中,∵∠AEO=90°,∠AOE=30°,
∴OE===2,
∴OB=OE+BE=2+2.
在直角△BOD中,∵∠ODB=90°,∠BOD=30°,
∴BD=OB=+.
故选:A.
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是( )
A.5米
B.6米
C.6.5米
D.12米
解:如图AC=13,作CB⊥AB,
∵cosα==,
∴AB=12,
∴BC===5,
∴小车上升的高度是5m.
故选:A.
7.如图,甲、乙二人同时从A地出发,甲沿北偏东50°方向行走200m后到达B地,并立即向正东方向走去,乙沿北偏东70°方向行走,二人恰好在C地相遇,则B、C两地的距离为( )
A.100m
B.150m
C.200m
D.无法确定
解:延长CB交y轴于E.
∵∠AEB=90°,∠EAB=50°,
∴∠EBA=40°,
∵∠EAC=70°,
∴∠BAC=20°,
∵∠EBA=∠BAC+∠C,
∴∠C=∠BAC=20°,
∴BA=BC=200m,
故选:C.
8.如图,已知45°<∠A<90°,则下列各式成立的是( )
A.sinA=cosA
B.sinA>cosA
C.sinA>tanA
D.sinA<cosA
解:∵45°<∠A<90°,
∴AC<BC,
sinA=,cosA=,tanA=,
∴cosA<sinA<tanA,
故选:B.
9.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为( )
A.800?sin32°
B.
C.800?tan32°
D.
解:如图,作BC⊥AC,垂足为C.
在Rt△ABC中,∠ACB=90°,
∠BAC=32°,AB=50×16=800(米),
sin∠BAC=,
∴BC=sin∠BAC?AB=800?sin32°.
故选:A.
10.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米
B.10米
C.20米
D.米
解:∵在直角三角形ADB中,∠D=30°,
∴=tan30°
∴BD==AB
∵在直角三角形ABC中,∠ACB=60°,
∴BC==AB
∵CD=20
∴CD=BD﹣BC=AB﹣AB=20
解得:AB=10.
故选:A.
二.填空题(共6小题)
11.在Rt△ABC中,∠C=90°,AB=4,BC=2,则sin= .
解:∵在Rt△ABC中,∠C=90°,AB=4,BC=2,
∴sinA=,
∴∠A=60°,
∴sin=sin30°=,
故答案为:.
12.小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了 25 m.
解:如图,过点B作BE⊥AC于点E,
∵坡度:i=1:,
∴tan∠A=1:=,
∴∠A=30°,
∵AB=50m,
∴BE=AB=25(m).
∴他升高了25m.
故答案为:25.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是 40 .
解:已知如图DE⊥AB,垂足是E,
所以△AED为直角三角形,
则得:sinA=,
即:=,
∴AD=10,
∴菱形ABCD的周长为:10×4=40.
故答案为:40.
14.如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 4 .
解:∵在直角△AOE中,cos∠EAC=,
∴OA===2,
又∵四边形ABCD是平行四边形,
∴AC=2OA=4.
故答案是:4.
15.如图,在地面上的点A处测得树顶B的仰角为α度,AC=6米,则树高BC为 6tanα 米(用含α的代数式表示).
解:过点B作BC⊥AC于点C,
在Rt△ABC中,
∵AC=6,∠A=α,
∴BC=ACtanα=6tanα.
故答案为:6tanα
16.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为 24.1 米(≈1.73,结果精确到0.1).
解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,
∴CE=33,
∵∠CBE=45°=∠BCE,∠CAE=30°,
∴BE=CE=33,
∴AE=a+33,
∵tanA=,
∴tan30°=,即33=a+33,
解得a=33(﹣1)≈24.1,
∴a的值约为24.1米,
故答案为:24.1.
三.解答题(共4小题)
17.计算题“
(1);
(2).
解:(1)原式=1+﹣3=﹣;
(2)原式=+1﹣+1﹣=.
18.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
(1)若AD=10,sin∠ADC=,求AC的长和tanB的值;
(2)如图,若∠B=a,AD=BD=1,则可以利用该图求出sin2a与a的三角函数之间的等量关系(用sina和cosa的值表示).
解:(1)在Rt△ACD中,∵sin∠ADC==,
而AD=10,
∴AC=8;
∴CD==6,
∵AB的垂直平分线与BC,AB的交点分别为D,E,
∴DB=DA=10,
∴BC=CD+DB=16,
在Rt△ABC中,tanB===;
(2)∵DA=DB,
∴∠DAB=∠B=α,
∴∠ADC=2∠B=2α,
∵sin∠ADC=,
∴AC=sin2α,
在Rt△BDE中,∵cosB=,
∴BE=cosα,
∴AB=2BE=2cosα,
在Rt△ABC中,∵sinB=,
∴AC=ABsinB,
∴sin2α=2cosα?sinα.
19.随着航母编队的成立,我国海军日益强大.2018年4月12日,中央军委在南海海域隆重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:≈1.414,≈1.732,结果精确到1海里).
解:在△APC中,∠ACP=90°,∠APC=45°,则AC=PC.
∵AP=400海里,
∴由勾股定理知,AP2=AC2+PC2=2PC2,即4002=2PC2,
故PC=200海里.
又∵在直角△BPC中,∠PCB=90°,∠BPC=60°,
∴PB==2PC=400≈566(海里).
答:此时巡逻舰与观测点P的距离PB约为566海里.
20.衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
解:如图,由题意∠CAB=30°,∠CBD=60°,DF=AE=1.5米
∵∠CBD=∠CAB+∠ACB,
∴∠ACB=∠CAB=30°,
∴AB=BC=10.4米,
在Rt△CBD中,CD=BC?sin60°=10.4?≈9.0米,
∴来雁塔的高度=CD+DF=9.0+1.5=10.5米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第26章
解直角三角形
易错题汇编
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,AB=4,AC=1,那么∠B的余弦值为( )
A.
B.
C.
D.
2.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35°
B.mcos35°
C.
D.
4.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m
B.50m
C.50m
D.m
5.如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A.(+)海里
B.2海里
C.(+1)海里
D.2海里
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是( )
A.5米
B.6米
C.6.5米
D.12米
7.如图,甲、乙二人同时从A地出发,甲沿北偏东50°方向行走200m后到达B地,并立即向正东方向走去,乙沿北偏东70°方向行走,二人恰好在C地相遇,则B、C两地的距离为( )
A.100m
B.150m
C.200m
D.无法确定
8.如图,已知45°<∠A<90°,则下列各式成立的是( )
A.sinA=cosA
B.sinA>cosA
C.sinA>tanA
D.sinA<cosA
9.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为( )
A.800?sin32°
B.
C.800?tan32°
D.
10.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米
B.10米
C.20米
D.米
二.填空题(共6小题)
11.在Rt△ABC中,∠C=90°,AB=4,BC=2,则sin=
.
12.小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了
m.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是
.
14.如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于
.
15.如图,在地面上的点A处测得树顶B的仰角为α度,AC=6米,则树高BC为
米(用含α的代数式表示).
16.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为
米(≈1.73,结果精确到0.1).
三.解答题(共4小题)
17.计算题“
(1);
(2).
18.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
(1)若AD=10,sin∠ADC=,求AC的长和tanB的值;
(2)如图,若∠B=a,AD=BD=1,则可以利用该图求出sin2a与a的三角函数之间的等量关系(用sina和cosa的值表示).
19.随着航母编队的成立,我国海军日益强大.2018年4月12日,中央军委在南海海域隆重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:≈1.414,≈1.732,结果精确到1海里).
20.衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
试题解析
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,AB=4,AC=1,那么∠B的余弦值为( )
A.
B.
C.
D.
解;由勾股定理得BC===,
cos∠B==,
故选:A.
2.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A.
B.
C.
D.
解:由tan∠B=,得
AC=BC?tanB=5×tan26.
故选:D.
3.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A.msin35°
B.mcos35°
C.
D.
解:sin∠A=,
∵AB=m,∠A=35°,
∴BC=msin35°,
故选:A.
4.如图,某地修建高速公路,要从B地向C地修一座隧道(B、C在同一水平面上).为了测量B、C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升100m到达A处,在A处观察B地的俯角为30°,则B、C两地之间的距离为( )
A.100m
B.50m
C.50m
D.m
解:根据题意得:∠ABC=30°,AC⊥BC,AC=100m,
在Rt△ABC中,BC===100(m).
故选:A.
5.如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A.(+)海里
B.2海里
C.(+1)海里
D.2海里
解:如图,作BD⊥OC于D,则船A离灯塔B的最近距离是BD的长.作AE⊥OB于E.
在直角△ABE中,∵∠AEB=90°,∠ABE=∠BAD﹣∠AOB=75°﹣30°=45°,AB=4,
∴AE=BE=AB=2.
在直角△AOE中,∵∠AEO=90°,∠AOE=30°,
∴OE===2,
∴OB=OE+BE=2+2.
在直角△BOD中,∵∠ODB=90°,∠BOD=30°,
∴BD=OB=+.
故选:A.
6.如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=,则小车上升的高度是( )
A.5米
B.6米
C.6.5米
D.12米
解:如图AC=13,作CB⊥AB,
∵cosα==,
∴AB=12,
∴BC===5,
∴小车上升的高度是5m.
故选:A.
7.如图,甲、乙二人同时从A地出发,甲沿北偏东50°方向行走200m后到达B地,并立即向正东方向走去,乙沿北偏东70°方向行走,二人恰好在C地相遇,则B、C两地的距离为( )
A.100m
B.150m
C.200m
D.无法确定
解:延长CB交y轴于E.
∵∠AEB=90°,∠EAB=50°,
∴∠EBA=40°,
∵∠EAC=70°,
∴∠BAC=20°,
∵∠EBA=∠BAC+∠C,
∴∠C=∠BAC=20°,
∴BA=BC=200m,
故选:C.
8.如图,已知45°<∠A<90°,则下列各式成立的是( )
A.sinA=cosA
B.sinA>cosA
C.sinA>tanA
D.sinA<cosA
解:∵45°<∠A<90°,
∴AC<BC,
sinA=,cosA=,tanA=,
∴cosA<sinA<tanA,
故选:B.
9.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,则山的高度BC为( )
A.800?sin32°
B.
C.800?tan32°
D.
解:如图,作BC⊥AC,垂足为C.
在Rt△ABC中,∠ACB=90°,
∠BAC=32°,AB=50×16=800(米),
sin∠BAC=,
∴BC=sin∠BAC?AB=800?sin32°.
故选:A.
10.如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10米
B.10米
C.20米
D.米
解:∵在直角三角形ADB中,∠D=30°,
∴=tan30°
∴BD==AB
∵在直角三角形ABC中,∠ACB=60°,
∴BC==AB
∵CD=20
∴CD=BD﹣BC=AB﹣AB=20
解得:AB=10.
故选:A.
二.填空题(共6小题)
11.在Rt△ABC中,∠C=90°,AB=4,BC=2,则sin= .
解:∵在Rt△ABC中,∠C=90°,AB=4,BC=2,
∴sinA=,
∴∠A=60°,
∴sin=sin30°=,
故答案为:.
12.小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了 25 m.
解:如图,过点B作BE⊥AC于点E,
∵坡度:i=1:,
∴tan∠A=1:=,
∴∠A=30°,
∵AB=50m,
∴BE=AB=25(m).
∴他升高了25m.
故答案为:25.
13.如图,在菱形ABCD中,DE⊥AB,垂足是E,DE=6,sinA=,则菱形ABCD的周长是 40 .
解:已知如图DE⊥AB,垂足是E,
所以△AED为直角三角形,
则得:sinA=,
即:=,
∴AD=10,
∴菱形ABCD的周长为:10×4=40.
故答案为:40.
14.如图,?ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于 4 .
解:∵在直角△AOE中,cos∠EAC=,
∴OA===2,
又∵四边形ABCD是平行四边形,
∴AC=2OA=4.
故答案是:4.
15.如图,在地面上的点A处测得树顶B的仰角为α度,AC=6米,则树高BC为 6tanα 米(用含α的代数式表示).
解:过点B作BC⊥AC于点C,
在Rt△ABC中,
∵AC=6,∠A=α,
∴BC=ACtanα=6tanα.
故答案为:6tanα
16.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为 24.1 米(≈1.73,结果精确到0.1).
解:如图,设CD为塔身的高,延长AB交CD于E,则CD=40,DE=7,
∴CE=33,
∵∠CBE=45°=∠BCE,∠CAE=30°,
∴BE=CE=33,
∴AE=a+33,
∵tanA=,
∴tan30°=,即33=a+33,
解得a=33(﹣1)≈24.1,
∴a的值约为24.1米,
故答案为:24.1.
三.解答题(共4小题)
17.计算题“
(1);
(2).
解:(1)原式=1+﹣3=﹣;
(2)原式=+1﹣+1﹣=.
18.如图,在Rt△ABC中,∠C=90°,AB的垂直平分线与BC,AB的交点分别为D,E.
(1)若AD=10,sin∠ADC=,求AC的长和tanB的值;
(2)如图,若∠B=a,AD=BD=1,则可以利用该图求出sin2a与a的三角函数之间的等量关系(用sina和cosa的值表示).
解:(1)在Rt△ACD中,∵sin∠ADC==,
而AD=10,
∴AC=8;
∴CD==6,
∵AB的垂直平分线与BC,AB的交点分别为D,E,
∴DB=DA=10,
∴BC=CD+DB=16,
在Rt△ABC中,tanB===;
(2)∵DA=DB,
∴∠DAB=∠B=α,
∴∠ADC=2∠B=2α,
∵sin∠ADC=,
∴AC=sin2α,
在Rt△BDE中,∵cosB=,
∴BE=cosα,
∴AB=2BE=2cosα,
在Rt△ABC中,∵sinB=,
∴AC=ABsinB,
∴sin2α=2cosα?sinα.
19.随着航母编队的成立,我国海军日益强大.2018年4月12日,中央军委在南海海域隆重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:≈1.414,≈1.732,结果精确到1海里).
解:在△APC中,∠ACP=90°,∠APC=45°,则AC=PC.
∵AP=400海里,
∴由勾股定理知,AP2=AC2+PC2=2PC2,即4002=2PC2,
故PC=200海里.
又∵在直角△BPC中,∠PCB=90°,∠BPC=60°,
∴PB==2PC=400≈566(海里).
答:此时巡逻舰与观测点P的距离PB约为566海里.
20.衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
解:如图,由题意∠CAB=30°,∠CBD=60°,DF=AE=1.5米
∵∠CBD=∠CAB+∠ACB,
∴∠ACB=∠CAB=30°,
∴AB=BC=10.4米,
在Rt△CBD中,CD=BC?sin60°=10.4?≈9.0米,
∴来雁塔的高度=CD+DF=9.0+1.5=10.5米.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
