1.1探索勾股定理 同步练习(含解析)
文档属性
| 名称 | 1.1探索勾股定理 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-28 10:21:39 | ||
图片预览



文档简介
初中数学北师大版八年级上学期 第一章 1.1探索勾股定理
一、单选题
1.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB= ,则图中阴影部分的面积为(? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?5
2.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB的长为(??? )
A.?5??????????????????????????????????????????B.?25??????????????????????????????????????????C.?6??????????????????????????????????????????D.?
3.如图,以Rt△ ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3 , 若S1+S2+S3=16,则S1的值为( ???)
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
4.下列说法正确的是( )
A.?若 a、b、c是△ABC的三边,则a2+b2=c2
B.?若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.?若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.?若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
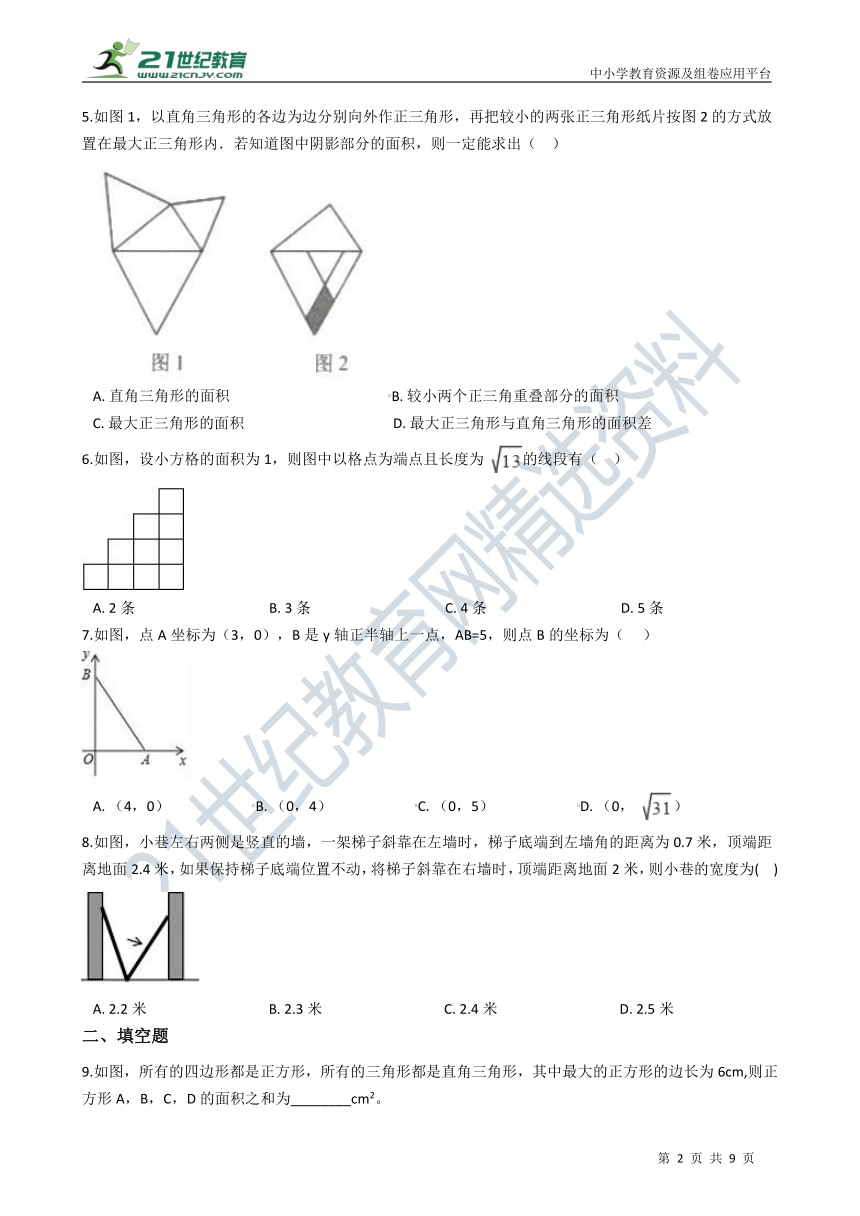
5.如图1,以直角三角形的各边为边分别向外作正三角形,再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出(?? )
A.?直角三角形的面积??????????????????????????????????????????????B.?较小两个正三角重叠部分的面积
C.?最大正三角形的面积???????????????????????????????????????????D.?最大正三角形与直角三角形的面积差
6.如图,设小方格的面积为1,则图中以格点为端点且长度为 的线段有(?? )
A.?2条???????????????????????????????????????B.?3条???????????????????????????????????????C.?4条???????????????????????????????????????D.?5条
7.如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( ???)
A.?(4,0)????????????????????????B.?(0,4)????????????????????????C.?(0,5)????????????????????????D.?(0, )
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为(?? )
A.?2.2米???????????????????????????????????B.?2.3米???????????????????????????????????C.?2.4米???????????????????????????????????D.?2.5米
二、填空题
9.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为6cm,则正方形A,B,C,D的面积之和为________cm2。
10.生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的 时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?________(填“能”或“不能”).
11.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为10 cm2和26 cm2 , 则正方形A的边长是________cm.
12.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
三、综合题
13.如图网格是由边长为1的小正方形组成,点A、B、C位置如图所示,在网格中确定点D,使以A、B、C、D为顶点的四边形的所有内角都相等。
(1)确定点D的位置,并画出以A、B、C、D为顶点的四边形,并说明理由;
(2)求出(1)中所画出的四边形的周长和面积。
14.如图,△ ABC中,CD是AB边上的高,CD=12,AC=20,BC=15,AE=AC,BF=BC,求EF的长.
15.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:
(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
答案解析部分
一、单选题
1.【答案】 D
解: ,
∵在Rt△ABC中,AB2=AC2+BC2= ,
∴AB2+AC2+BC2=10,
∴S阴影= ×10=5.
故答案为:D.
【分析】先用直角三角形的边长表示出阴影部分的面积,再根据勾股定理可得:AB2=AC2+BC2 , 进而可将阴影部分的面积求出.
2.【答案】 A
解:在Rt△ABC中,∠C=90°,
∴
故答案为:A.
【分析】利用勾股定理求解即可.
3.【答案】 B
解:根据勾股定理可知,AC2+BC2=AB2
∴S3+S2=S1
∵S3+S2+S1=16
∴2S1=16
∴S1=8
故答案为:B.
【分析】在直角三角形中,根据勾股定理,即可得到三个正方形面积的和为16,求出S1的答案即可。
4.【答案】 C
A. 若 a、b、c是△ABC的三边,但△ABC不一定是直角三角形,则a2+b2不一定等于c2 , 故本选项错误;
B. 若 a、b、c是Rt△ABC的三边,但不确定哪条边为斜边,则a2+b2不一定等于c2 , 故本选项错误;
C. 若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2 , 故本选项正确;
D. 若 a、b、c是Rt△ABC的三边, ,则c2+b2=a2 , 故本选项错误.
故答案为:C.
【分析】根据勾股定理:直角三角形中的两直角边的平方之和等于斜边的平方逐一判断即可.
5.【答案】 B
解:设直角三角形的斜边长为c,较短直角边长为a,较长直角边为b,
由勾股定理得:c2=a2+b2 ,
阴影部分的面积为:,
较小两个正三角形重叠部分的边长为:a+b-c,
则较小两个正三角形重叠部分的面积为:
,
∴知道图中阴影部分的面积,则一定能求出较小两个正三角形重叠部分的面积,即等于阴影部分的面积.
故答案为:B.
【分析】根据勾股定理得到c2=a2+b2 , 再根据正三角形的面积公式、平行四边形的面积公式推导计算即可.
6.【答案】 D
由题意和分析可画图如下:
故答案为:D.
【分析】根据勾股定理,可以将13分为4+9即22+32,只要找到边长为2和3的直角三角形即可.
7.【答案】 B
解:因为点A坐标为(3,0),B是y轴正半轴上一点,AB=5,
所以OB= =4 ,
所以点B的坐标为(0,4),
故答案为:B.
【分析】根据勾股定理算出OB的长,再根据点的坐标与图形的性质即可得出点B的坐标.
8.【答案】 A
解:如图,
在Rt△ACB中,
∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴
在Rt△A'BD中,
∵∠A'BD=90°,A'D=2米,
∴
∴
∵BD>0,
∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2米
即小巷的宽度为2.2米,
故答案为:A.
【分析】如图,在Rt△ACB中,genuine勾股定理表示出AB2 , 在Rt△A'BD中,利用勾股定理即可求出BD的长,进而根据CD=BC+BD算出答案.
二、填空题
9.【答案】 36
如右图所示,
根据勾股定理可知,
,
,
∴ ,
故答案为:36.
【分析】根据勾股定理有, , ,等量代换即可求四个小正方形的面积之和.
10.【答案】 不能
解:∵梯子底端离墙约为梯子长度的 ,且梯子的长度为9米,
∴梯子底端离墙约为梯子长度为9× =3米,
∴梯子的顶端距离地面的高度为: ,
∵ ,
∴梯子的顶端不能到达8.5米高的墙头.
故答案为:不能.
【分析】根据梯子的长度得到梯子距离墙面的距离,然后用勾股定理求出梯子的顶端距离地面的高度后与8.5比较即可作出判断.
11.【答案】 4
如图所示:
根据题意得: =26, =10,∠EFG=90°,
根据勾股定理得:
∴正方形A的边长为: .
故答案为: .
【分析】根据已知两正方形的面积分别得出直角三角形两直角边长的平方,利用勾股定理求出斜边长的平方,即可求出正方形A的面积.
12.【答案】 8
解:由题意得,斜边长AB= = =10米,
则少走(6+8-10)×2=8步路,
故答案为:8.
【分析】先根据勾股定理求出斜边的长,与直角边进行比较即可求得结果。
三、综合题
13.【答案】 (1)解:如图所示
AB= = =DC
BC= =2 =AD
所以,四边形ABCD是平行四边形。
又因为 ,所以
所以四边形ABCD是矩形,故四个内角相等。
(2)解:周长为(2 + )×2=6
面积为2 × =10
【分析】(1)根据题意可知,四边形的内角为直角,得到D点的位置即可;
(2)根据勾股定理计算得到AB和BC的长度,根据周长公式求出答案即可。
14.【答案】 解:∵CD是高
∴∠CDB=∠BDC=90°
在Rt△ADC中,,
在Rt△BDC中,,
∵AE=AC=20,
∴DE=AE-AD=20-16=4,
∵BF=BC=15,
∴DF=BF-BD=15-9=6,
∴EF=DE+DF=4+6=10.
【分析】利用三角形的高的定义,可知∠CDB=∠BDC=90°,再利用勾股定理求出AD,BD的长,利用已知条件求出DE,DF的长,然后根据EF=DE+DF,即可求出EF的长。
15.【答案】 (1)解:在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2 , AC2=AD2+CD2 ,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)解:∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2 ,
∴△ABC不是直角三角形.
【分析】(1)?已知AD、BD、CD,?在Rt△ABD和Rt△ACD中,分别由勾股定理求得AB和AC,BC=BD+DC长度可求,则 △ABC的周长可求;
(2)先找出最大边,再求较小两边的平方和,利用勾股定理的逆定理判断即可。
一、单选题
1.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB= ,则图中阴影部分的面积为(? )
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?????????????????????????????????????????D.?5
2.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则AB的长为(??? )
A.?5??????????????????????????????????????????B.?25??????????????????????????????????????????C.?6??????????????????????????????????????????D.?
3.如图,以Rt△ ABC的三边为边,分别向外作正方形,它们的面积分别为S1、S2、S3 , 若S1+S2+S3=16,则S1的值为( ???)
A.?7???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
4.下列说法正确的是( )
A.?若 a、b、c是△ABC的三边,则a2+b2=c2
B.?若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.?若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
D.?若 a、b、c是Rt△ABC的三边,,则a2+b2=c2
5.如图1,以直角三角形的各边为边分别向外作正三角形,再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出(?? )
A.?直角三角形的面积??????????????????????????????????????????????B.?较小两个正三角重叠部分的面积
C.?最大正三角形的面积???????????????????????????????????????????D.?最大正三角形与直角三角形的面积差
6.如图,设小方格的面积为1,则图中以格点为端点且长度为 的线段有(?? )
A.?2条???????????????????????????????????????B.?3条???????????????????????????????????????C.?4条???????????????????????????????????????D.?5条
7.如图,点A坐标为(3,0),B是y轴正半轴上一点,AB=5,则点B的坐标为( ???)
A.?(4,0)????????????????????????B.?(0,4)????????????????????????C.?(0,5)????????????????????????D.?(0, )
8.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为(?? )
A.?2.2米???????????????????????????????????B.?2.3米???????????????????????????????????C.?2.4米???????????????????????????????????D.?2.5米
二、填空题
9.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为6cm,则正方形A,B,C,D的面积之和为________cm2。
10.生活经验表明:靠墙摆放梯子时,若梯子底端离墙约为梯子长度的 时,则梯子比较稳定.现有一长度为9 m的梯子,当梯子稳定摆放时,它的顶端能到达8.5 m高的墙头吗?________(填“能”或“不能”).
11.如图,分别以直角三角形各边为一边向三角形外部作正方形,其中两个正方形的面积分别为10 cm2和26 cm2 , 则正方形A的边长是________cm.
12.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了________步路(假设2步为1米),却踩伤了花草.
三、综合题
13.如图网格是由边长为1的小正方形组成,点A、B、C位置如图所示,在网格中确定点D,使以A、B、C、D为顶点的四边形的所有内角都相等。
(1)确定点D的位置,并画出以A、B、C、D为顶点的四边形,并说明理由;
(2)求出(1)中所画出的四边形的周长和面积。
14.如图,△ ABC中,CD是AB边上的高,CD=12,AC=20,BC=15,AE=AC,BF=BC,求EF的长.
15.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
求:
(1)△ABC的周长;
(2)判断△ABC是否是直角三角形?为什么?
答案解析部分
一、单选题
1.【答案】 D
解: ,
∵在Rt△ABC中,AB2=AC2+BC2= ,
∴AB2+AC2+BC2=10,
∴S阴影= ×10=5.
故答案为:D.
【分析】先用直角三角形的边长表示出阴影部分的面积,再根据勾股定理可得:AB2=AC2+BC2 , 进而可将阴影部分的面积求出.
2.【答案】 A
解:在Rt△ABC中,∠C=90°,
∴
故答案为:A.
【分析】利用勾股定理求解即可.
3.【答案】 B
解:根据勾股定理可知,AC2+BC2=AB2
∴S3+S2=S1
∵S3+S2+S1=16
∴2S1=16
∴S1=8
故答案为:B.
【分析】在直角三角形中,根据勾股定理,即可得到三个正方形面积的和为16,求出S1的答案即可。
4.【答案】 C
A. 若 a、b、c是△ABC的三边,但△ABC不一定是直角三角形,则a2+b2不一定等于c2 , 故本选项错误;
B. 若 a、b、c是Rt△ABC的三边,但不确定哪条边为斜边,则a2+b2不一定等于c2 , 故本选项错误;
C. 若 a、b、c是Rt△ABC的三边, ,则a2+b2=c2 , 故本选项正确;
D. 若 a、b、c是Rt△ABC的三边, ,则c2+b2=a2 , 故本选项错误.
故答案为:C.
【分析】根据勾股定理:直角三角形中的两直角边的平方之和等于斜边的平方逐一判断即可.
5.【答案】 B
解:设直角三角形的斜边长为c,较短直角边长为a,较长直角边为b,
由勾股定理得:c2=a2+b2 ,
阴影部分的面积为:,
较小两个正三角形重叠部分的边长为:a+b-c,
则较小两个正三角形重叠部分的面积为:
,
∴知道图中阴影部分的面积,则一定能求出较小两个正三角形重叠部分的面积,即等于阴影部分的面积.
故答案为:B.
【分析】根据勾股定理得到c2=a2+b2 , 再根据正三角形的面积公式、平行四边形的面积公式推导计算即可.
6.【答案】 D
由题意和分析可画图如下:
故答案为:D.
【分析】根据勾股定理,可以将13分为4+9即22+32,只要找到边长为2和3的直角三角形即可.
7.【答案】 B
解:因为点A坐标为(3,0),B是y轴正半轴上一点,AB=5,
所以OB= =4 ,
所以点B的坐标为(0,4),
故答案为:B.
【分析】根据勾股定理算出OB的长,再根据点的坐标与图形的性质即可得出点B的坐标.
8.【答案】 A
解:如图,
在Rt△ACB中,
∵∠ACB=90°,BC=0.7米,AC=2.4米,
∴
在Rt△A'BD中,
∵∠A'BD=90°,A'D=2米,
∴
∴
∵BD>0,
∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2米
即小巷的宽度为2.2米,
故答案为:A.
【分析】如图,在Rt△ACB中,genuine勾股定理表示出AB2 , 在Rt△A'BD中,利用勾股定理即可求出BD的长,进而根据CD=BC+BD算出答案.
二、填空题
9.【答案】 36
如右图所示,
根据勾股定理可知,
,
,
∴ ,
故答案为:36.
【分析】根据勾股定理有, , ,等量代换即可求四个小正方形的面积之和.
10.【答案】 不能
解:∵梯子底端离墙约为梯子长度的 ,且梯子的长度为9米,
∴梯子底端离墙约为梯子长度为9× =3米,
∴梯子的顶端距离地面的高度为: ,
∵ ,
∴梯子的顶端不能到达8.5米高的墙头.
故答案为:不能.
【分析】根据梯子的长度得到梯子距离墙面的距离,然后用勾股定理求出梯子的顶端距离地面的高度后与8.5比较即可作出判断.
11.【答案】 4
如图所示:
根据题意得: =26, =10,∠EFG=90°,
根据勾股定理得:
∴正方形A的边长为: .
故答案为: .
【分析】根据已知两正方形的面积分别得出直角三角形两直角边长的平方,利用勾股定理求出斜边长的平方,即可求出正方形A的面积.
12.【答案】 8
解:由题意得,斜边长AB= = =10米,
则少走(6+8-10)×2=8步路,
故答案为:8.
【分析】先根据勾股定理求出斜边的长,与直角边进行比较即可求得结果。
三、综合题
13.【答案】 (1)解:如图所示
AB= = =DC
BC= =2 =AD
所以,四边形ABCD是平行四边形。
又因为 ,所以
所以四边形ABCD是矩形,故四个内角相等。
(2)解:周长为(2 + )×2=6
面积为2 × =10
【分析】(1)根据题意可知,四边形的内角为直角,得到D点的位置即可;
(2)根据勾股定理计算得到AB和BC的长度,根据周长公式求出答案即可。
14.【答案】 解:∵CD是高
∴∠CDB=∠BDC=90°
在Rt△ADC中,,
在Rt△BDC中,,
∵AE=AC=20,
∴DE=AE-AD=20-16=4,
∵BF=BC=15,
∴DF=BF-BD=15-9=6,
∴EF=DE+DF=4+6=10.
【分析】利用三角形的高的定义,可知∠CDB=∠BDC=90°,再利用勾股定理求出AD,BD的长,利用已知条件求出DE,DF的长,然后根据EF=DE+DF,即可求出EF的长。
15.【答案】 (1)解:在Rt△ABD和Rt△ACD中,
根据勾股定理得:AB2=AD2+BD2 , AC2=AD2+CD2 ,
又AD=12,BD=16,CD=5,
∴AB=20,AC=13,
△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
(2)解:∵AB=20,AC=13,BC=21,
AB2+AC2≠BC2 ,
∴△ABC不是直角三角形.
【分析】(1)?已知AD、BD、CD,?在Rt△ABD和Rt△ACD中,分别由勾股定理求得AB和AC,BC=BD+DC长度可求,则 △ABC的周长可求;
(2)先找出最大边,再求较小两边的平方和,利用勾股定理的逆定理判断即可。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
