人教版数学九年级上册22.3.2 实际问题与二次函数(二)——商品利润最大问题课件(共27张)
文档属性
| 名称 | 人教版数学九年级上册22.3.2 实际问题与二次函数(二)——商品利润最大问题课件(共27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 20:14:58 | ||
图片预览






文档简介
学习目标
能应用二次函数的性质解决商品销售过程中的最大利润问题.
弄清商品销售问题中的数量关系及确定自变量的取值范围.
在日常生活中存在着许许多多的与数学知识有关的实际问题.商品买卖过程中,作为商家追求利润最大化是永恒的追求.
如果你是商场经理,如何定价才能使商场获得最大利润呢?
情景引入
某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,则每星期销售额是 元,销售利润 元.
18000
6000
数量关系
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
情景引入
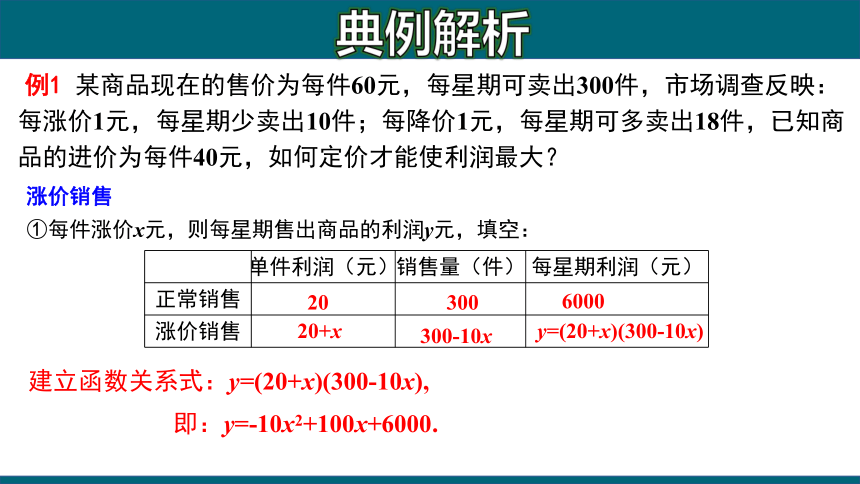
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
典例解析
1.自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
2.涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
典例解析
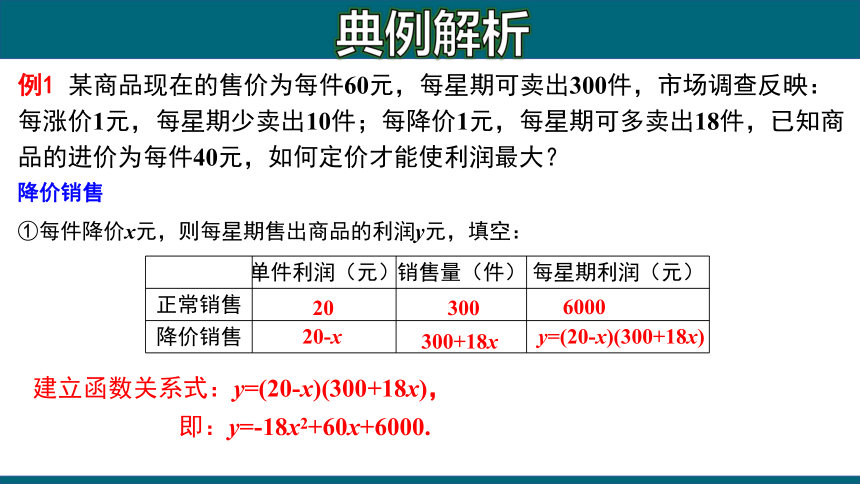
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
6000
典例解析
综合可知,应定价65元时,才能使利润最大.
1.自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
2.降价多少元时,利润最大,是多少?
当 时,
即定价57.5元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?
典例解析
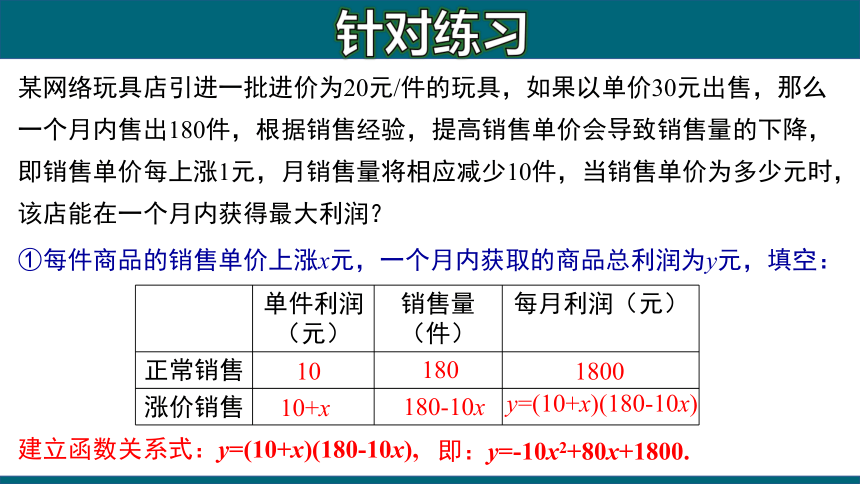
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?
①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每月利润(元)
正常销售
涨价销售
10
180
10+x
180-10x
y=(10+x)(180-10x)
1800
建立函数关系式:y=(10+x)(180-10x),
即:y=-10x2+80x+1800.
针对练习
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x ≥0,因此自变量的取值范围是x ≤18.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+80x+1800 = -10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960元.
答:当销售单价为34元时,该店在一个月内能获得最大利润1960元.
②自变量x的取值范围如何确定?
针对练习
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
归纳总结
例2 某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
典例解析
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
典例解析
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
典例解析
解:∵当40≤x≤50时, Q最大= 1200<1218
当50≤x≤70时, Q最大= 1250>1218
∴售价x应在50~70元之间.
∴令:-2(x-55)2 +1250=1218
解得:x1=51,x2=59
当x1=51时,y1=-2x+160=-2×51+160= 58(件)
当x2=59时,y2=-2x+160= -2×59+160= 42(件)
∴若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.
(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?
典例解析
变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:Q与x的函数关系式为:
60x-1800 (40≤x≤50 )
-2(x-55)2 + 1250 (50≤x≤70)
Q =
由例3可知:
若40≤x≤50, 则当x=50时,Q最大= 1200
若50≤x≤70, 则当x=55时,Q最大= 1250
∵1200<1250
∴售价x是55元时,获利最大,最大利润是1250元.
变式练习
(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,
∵Q最大= 1200<1218,
∴此情况不存在.
60x-1800 (40≤x≤50 )
-2(x-55)2 + 1250 (50≤x≤70)
Q =
变式练习
②当50≤x≤70时,
Q最大= 1250>1218,
令Q = 1218,得
-2(x-55)2 +1250=1218
解得:x1=51,x2=59
由Q = -2(x-55)2 +1250的
图象和性质可知:
当51≤x≤59时,Q≥1218
∴若该商品所获利润不低于1218元,
则售价x的取值范围为51≤x≤59.
x
Q
0
55
1218
59
51
1250
变式练习
(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得:
51≤x≤59
30 (-2 x +160)≥1620
解得:51≤x≤53
变式练习
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,
Q随x的增大而增大
∴当x最大 = 53时,Q最大= 1242
∴此时售价x应定为53元,
利润最大,最大利润是1242元.
x
Q
0
55
1242
53
51
变式练习
1.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为 元.
25
2.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
达标检测
3.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
达标检测
w=[12+2(x-1)][80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
解:设生产x档次的产品时,每天所获得的利润为w元,
则
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次产品,可使利润最大,
最大利润为1352.
达标检测
x
y
5
16
O
7
4. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
达标检测
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
达标检测
小结梳理
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
能应用二次函数的性质解决商品销售过程中的最大利润问题.
弄清商品销售问题中的数量关系及确定自变量的取值范围.
在日常生活中存在着许许多多的与数学知识有关的实际问题.商品买卖过程中,作为商家追求利润最大化是永恒的追求.
如果你是商场经理,如何定价才能使商场获得最大利润呢?
情景引入
某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,则每星期销售额是 元,销售利润 元.
18000
6000
数量关系
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
情景引入
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售
①每件涨价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
涨价销售
20
300
20+x
300-10x
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
6000
典例解析
1.自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
2.涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
当 时,y=-10×52+100×5+6000=6250.
即定价65元时,最大利润是6250元.
典例解析
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
降价销售
①每件降价x元,则每星期售出商品的利润y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每星期利润(元)
正常销售
降价销售
20
300
20-x
300+18x
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即:y=-18x2+60x+6000.
6000
典例解析
综合可知,应定价65元时,才能使利润最大.
1.自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
2.降价多少元时,利润最大,是多少?
当 时,
即定价57.5元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?
典例解析
某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?
①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
单件利润(元)
销售量(件)
每月利润(元)
正常销售
涨价销售
10
180
10+x
180-10x
y=(10+x)(180-10x)
1800
建立函数关系式:y=(10+x)(180-10x),
即:y=-10x2+80x+1800.
针对练习
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x ≥0,因此自变量的取值范围是x ≤18.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+80x+1800 = -10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960元.
答:当销售单价为34元时,该店在一个月内能获得最大利润1960元.
②自变量x的取值范围如何确定?
针对练习
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
归纳总结
例2 某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时,
Q = 60(x-30)= 60x-1800
∵ y = 60 > 0,Q随x的增大而增大
∴当x最大= 50时,Q最大= 1200
答:此时每月的总利润最多是1200元.
典例解析
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时,
设y与x函数关系式为y=kx+b,
∵线段过(50,60)和(70,20).
50k+b=60
70k+b=20
∴
∴y =-2x +160(50≤x≤70)
解得:
k =-2
b = 160
典例解析
∴y =-2x +160(50≤x≤70)
∴Q=(x-30)y
=(x-30)(-2x + 160)
=-2x2 + 220x- 4800
=-2(x-55)2 +1250 (50≤x≤70)
∵a = -2<0,图象开口向下,
∴当x = 55时,Q最大= 1250
∴当售价在50~70元时,售价x是55元时,获利最大,
最大利润是1250元.
典例解析
解:∵当40≤x≤50时, Q最大= 1200<1218
当50≤x≤70时, Q最大= 1250>1218
∴售价x应在50~70元之间.
∴令:-2(x-55)2 +1250=1218
解得:x1=51,x2=59
当x1=51时,y1=-2x+160=-2×51+160= 58(件)
当x2=59时,y2=-2x+160= -2×59+160= 42(件)
∴若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.
(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?
典例解析
变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:Q与x的函数关系式为:
60x-1800 (40≤x≤50 )
-2(x-55)2 + 1250 (50≤x≤70)
Q =
由例3可知:
若40≤x≤50, 则当x=50时,Q最大= 1200
若50≤x≤70, 则当x=55时,Q最大= 1250
∵1200<1250
∴售价x是55元时,获利最大,最大利润是1250元.
变式练习
(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,
∵Q最大= 1200<1218,
∴此情况不存在.
60x-1800 (40≤x≤50 )
-2(x-55)2 + 1250 (50≤x≤70)
Q =
变式练习
②当50≤x≤70时,
Q最大= 1250>1218,
令Q = 1218,得
-2(x-55)2 +1250=1218
解得:x1=51,x2=59
由Q = -2(x-55)2 +1250的
图象和性质可知:
当51≤x≤59时,Q≥1218
∴若该商品所获利润不低于1218元,
则售价x的取值范围为51≤x≤59.
x
Q
0
55
1218
59
51
1250
变式练习
(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
解:由题意得:
51≤x≤59
30 (-2 x +160)≥1620
解得:51≤x≤53
变式练习
∵Q=-2(x-55)2 +1250的顶点
不在51≤x≤53范围内,
又∵a =-2<0,
∴当51≤x≤53时 ,
Q随x的增大而增大
∴当x最大 = 53时,Q最大= 1242
∴此时售价x应定为53元,
利润最大,最大利润是1242元.
x
Q
0
55
1242
53
51
变式练习
1.某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为 元.
25
2.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
达标检测
3.一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
达标检测
w=[12+2(x-1)][80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
解:设生产x档次的产品时,每天所获得的利润为w元,
则
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次产品,可使利润最大,
最大利润为1352.
达标检测
x
y
5
16
O
7
4. 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75.其图象如图.
(1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:(1)由题中条件可求y=-x2+20x-75
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.
即销售单价定为10元时,销售利润最
大,为25元;
达标检测
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)由对称性知y=16时,x=7和13.
故销售单价在7 ≤x ≤13时,利润不低于16元.
达标检测
小结梳理
求解最大利润问题的一般步骤
1.建立利润与价格之间的函数关系式:
运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
2.结合实际意义,确定自变量的取值范围;
3.在自变量的取值范围内确定最大利润:
可以利用配方法或公式求出最大利润;也可以画出函数的简图,利用简图和性质求出.
同课章节目录
