人教版数学九年级上册23.1.2 旋转作图课件(共25张)
文档属性
| 名称 | 人教版数学九年级上册23.1.2 旋转作图课件(共25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 20:17:48 | ||
图片预览




文档简介
学习目标
深入理解旋转及旋转图形的概念及性质.
能够根据旋转的基本性质解决实际问题和进行简单作图.
回顾平移的特征
A
B
C
D
E
F
G
H
K
L
M
N
经过平移:
1.新图形与原图形的形状、大小及方向完全相同;
2.对应点所连的线段平行(或在一条直线上)且相等;
3.对应线段平行(或在一条直线上)且相等;
4.对应角相等.
复习回顾
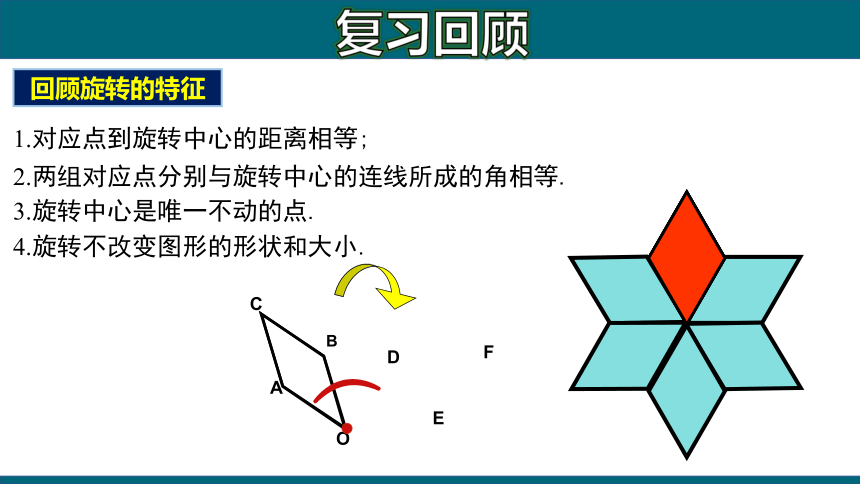
回顾旋转的特征
O
F
︵
A
B
C
D
E
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等.
3.旋转中心是唯一不动的点.
4.旋转不改变图形的形状和大小.
复习回顾
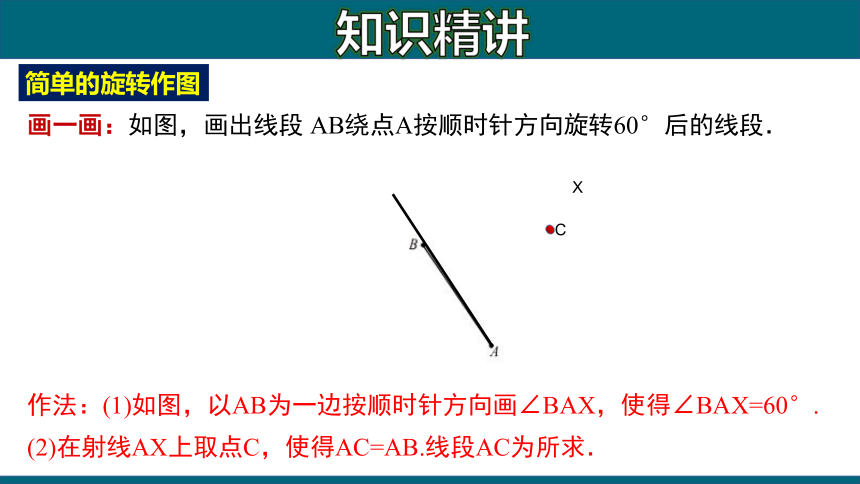
简单的旋转作图
画一画:如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
X
C
知识精讲
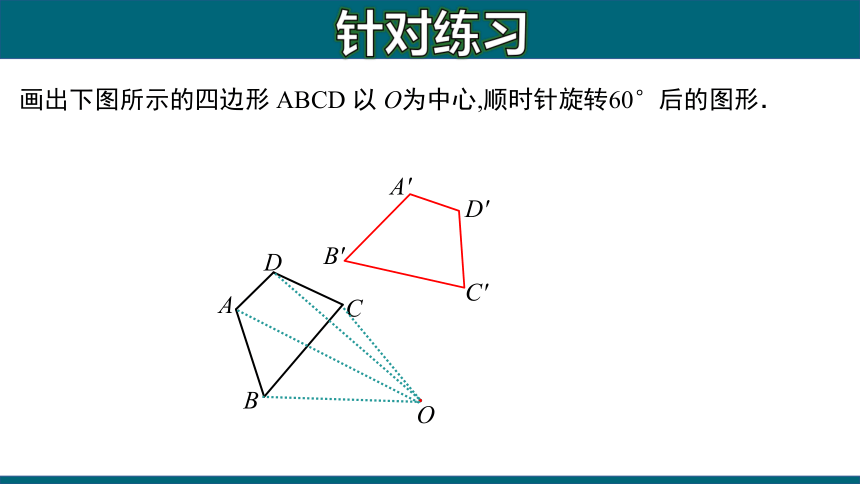
画出下图所示的四边形 ABCD 以 O为中心,顺时针旋转60°后的图形.
A
B
C
D
O
B'
A'
C'
D'
针对练习
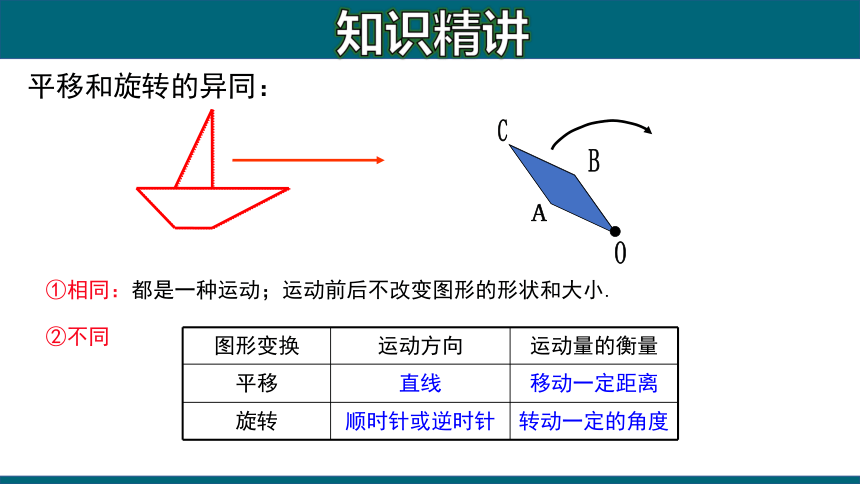
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
知识精讲
例1 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
作图关键-关键是确定点E的对应点E′
想一想:本题中作图的关键是什么?
A
B
C
D
E
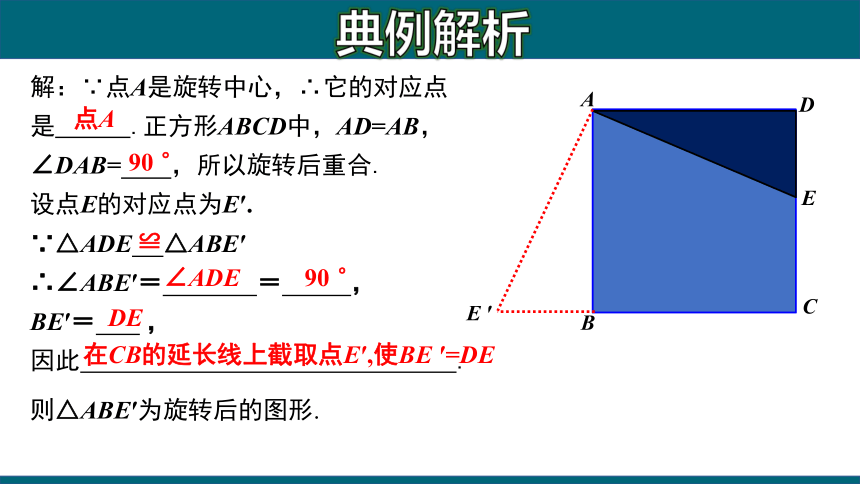
典例解析
解:∵点A是旋转中心,∴它的对应点是 .正方形ABCD中,AD=AB,∠DAB= ,所以旋转后重合.
设点E的对应点为E′.
∵△ADE △ABE′
∴∠ABE′= = ,
BE′= ,
因此 .
A
B
C
D
E
E ′
点A
90 °
≌
∠ADE
90 °
DE
在CB的延长线上截取点E′,使BE ′=DE
则△ABE′为旋转后的图形.
典例解析
答:延长CB,以点A为圆心,AE 的长为半径画弧,交CB的延长线于E',连接AE',则△ABE'为旋转后的图形.
A
B
C
D
E
思考:
还有其他方法确定点E的对应点E′吗?
(1)明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
归纳总结
D
E
B
F
C
A
考考你:
如图,如何确定它们的旋转中心位置?
答:找到两条对应点连线段的垂直平分线的交点.
O
知识精讲
A
B
O
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △O'A'B'吗?
A'
B'
针对练习
例2 怎样将甲图案变成乙图案?
甲
甲
乙
乙
A
B
B
A
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案.
还可以用什么方法把甲图案变成乙图案?
典例解析
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
平移:
平移的方向
平移的距离
仅靠平移无法得到
观察思考
旋转:
旋转中心
旋转角
旋转方向
O
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
整个图形可以看作是右边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的.
观察思考
平移、 旋转相结合:
先平移
后旋转
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
O
整个图形可以看作是右边的两个小“十字”先通过一次平移成图形左侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的.
观察思考
轴对称:
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
直线EF与GH相交于图形的中心O,且互相垂直,先把右边的两个“十字”作关于GH的轴对称图形,然后作这两部分关于EF的轴对称图形,这样就可以得到整个图形.
E
F
G
H
O
对称轴?
观察思考
如图,怎样将右边的图案变成左边的图案?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案.
针对练习
1.选择不同的__________、不同的______旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变, ______改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,产生了_______的旋转效果.
旋转中心
旋转角
旋转角
不同
旋转中心
不同
旋转设计作图
归纳总结
1.如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
针对练习
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD;
(4)连接EF,FG,GH,HE,
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
针对练习
2.如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
针对练习
小结梳理
深入理解旋转及旋转图形的概念及性质.
能够根据旋转的基本性质解决实际问题和进行简单作图.
回顾平移的特征
A
B
C
D
E
F
G
H
K
L
M
N
经过平移:
1.新图形与原图形的形状、大小及方向完全相同;
2.对应点所连的线段平行(或在一条直线上)且相等;
3.对应线段平行(或在一条直线上)且相等;
4.对应角相等.
复习回顾
回顾旋转的特征
O
F
︵
A
B
C
D
E
1.对应点到旋转中心的距离相等;
2.两组对应点分别与旋转中心的连线所成的角相等.
3.旋转中心是唯一不动的点.
4.旋转不改变图形的形状和大小.
复习回顾
简单的旋转作图
画一画:如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°.
(2)在射线AX上取点C,使得AC=AB.线段AC为所求.
X
C
知识精讲
画出下图所示的四边形 ABCD 以 O为中心,顺时针旋转60°后的图形.
A
B
C
D
O
B'
A'
C'
D'
针对练习
①相同:都是一种运动;运动前后不改变图形的形状和大小.
B
A
C
O
②不同
图形变换
运动方向
运动量的衡量
平移
直线
移动一定距离
旋转
顺时针或逆时针
转动一定的角度
平移和旋转的异同:
知识精讲
例1 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
作图关键-关键是确定点E的对应点E′
想一想:本题中作图的关键是什么?
A
B
C
D
E
典例解析
解:∵点A是旋转中心,∴它的对应点是 .正方形ABCD中,AD=AB,∠DAB= ,所以旋转后重合.
设点E的对应点为E′.
∵△ADE △ABE′
∴∠ABE′= = ,
BE′= ,
因此 .
A
B
C
D
E
E ′
点A
90 °
≌
∠ADE
90 °
DE
在CB的延长线上截取点E′,使BE ′=DE
则△ABE′为旋转后的图形.
典例解析
答:延长CB,以点A为圆心,AE 的长为半径画弧,交CB的延长线于E',连接AE',则△ABE'为旋转后的图形.
A
B
C
D
E
思考:
还有其他方法确定点E的对应点E′吗?
(1)明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
(2)找出关键点;
(3)作出关键点的对应点;
(4)作出新图形;
(5)写出结论.
归纳总结
D
E
B
F
C
A
考考你:
如图,如何确定它们的旋转中心位置?
答:找到两条对应点连线段的垂直平分线的交点.
O
知识精讲
A
B
O
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°, 你能画出△OAB 旋转后的图形 △O'A'B'吗?
A'
B'
针对练习
例2 怎样将甲图案变成乙图案?
甲
甲
乙
乙
A
B
B
A
可以先将甲图案绕图上的A点旋转,使得图案被“扶直”,然后,再沿AB方向将所得图案平移到B点位置,即可得到乙图案.
还可以用什么方法把甲图案变成乙图案?
典例解析
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
平移:
平移的方向
平移的距离
仅靠平移无法得到
观察思考
旋转:
旋转中心
旋转角
旋转方向
O
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
整个图形可以看作是右边的两个小“十字”绕着图案的中心旋转3次,分别旋转90°、180°、270°前后图形组成的.
观察思考
平移、 旋转相结合:
先平移
后旋转
下图由四部分组成,每部分都包括两个小“十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
O
整个图形可以看作是右边的两个小“十字”先通过一次平移成图形左侧的部分,然后左、右部分一起绕图形的中心旋转90°前后图形组成的.
观察思考
轴对称:
下图由四部分组成,每部分都包括两个小”十”字,红色部分能经过适当的旋转得到其他三部分吗?能经过平移吗?能经过轴对称吗?还有其他方式吗?
直线EF与GH相交于图形的中心O,且互相垂直,先把右边的两个“十字”作关于GH的轴对称图形,然后作这两部分关于EF的轴对称图形,这样就可以得到整个图形.
E
F
G
H
O
对称轴?
观察思考
如图,怎样将右边的图案变成左边的图案?
答:以右边图案的中心为旋转中心,将图案按逆时针方向旋转90°,然后平移,即可得到左边的图案.
针对练习
1.选择不同的__________、不同的______旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变, ______改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,产生了_______的旋转效果.
旋转中心
旋转角
旋转角
不同
旋转中心
不同
旋转设计作图
归纳总结
1.如图,四边形ABCD绕O点旋转后,顶点A的对应点为E,试确定B、C、D对应的点的位置,以及旋转后的四边形.
针对练习
解:(1)连接OA、OB、OC、OD、OE;
(2)分别以OB、OC、OD为一边作∠BOF, ∠COG, ∠DOH,使∠BOF= ∠COG= ∠DOH= ∠AOE;
(3)分别在射线OF,OG,OH上,截取OF=OB,OG=OC,OH=OD;
(4)连接EF,FG,GH,HE,
四边形EFGH就是四边形ABCD绕O点旋转后的图形.
针对练习
2.如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点D顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CD的
中点O旋转180°.
针对练习
小结梳理
同课章节目录
