人教版八年级上册数学第十一章《三角形》复习课件(共22张PPT)
文档属性
| 名称 | 人教版八年级上册数学第十一章《三角形》复习课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 663.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 20:05:27 | ||
图片预览








文档简介
(共22张PPT)
《三角形》复习用课件
知识点一:三角形的三边关系
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边;
知识点一:三角形的三边关系
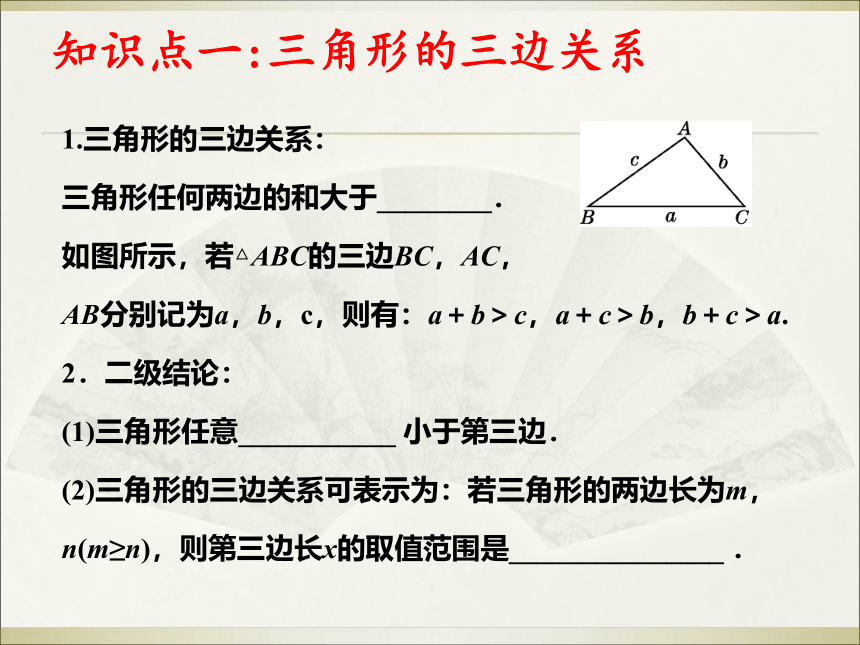
1.三角形的三边关系:
三角形任何两边的和大于________.
如图所示,若△ABC的三边BC,AC,
AB分别记为a,b,c,则有:a+b>c,a+c>b,b+c>a.
2.二级结论:
(1)三角形任意___________
小于第三边.
(2)三角形的三边关系可表示为:若三角形的两边长为m,
n(m≥n),则第三边长x的取值范围是_______________
.
知识点一:三角形的三边关系
例1.判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1).2,3,5
(2).2,3,6
(3).3,4,5
要判断三条线段能否组成三角形,依据“三角形任
何两边的和
大于第三边”,只要把最长的一条线段
与另外两条线段的和作比较.如果最
长的一条线段
小于另外两条线段的和,那么这三条线段就能组成
三角形;
如果最长的一条线段大于或等于另外两条
线段的和,那么这三条线段就不
能组成三角形.
答案(3)
知识点一:三角形的三边关系
例2.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
根据三角形的三边关系即可求出x的取值范围.
解答:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.∴选A.
知识点一:三角形的三边关系
变式练习:
1.若三角形三边长为2,4,m,则m的值不可以是(
)
A.3
B.4
C.5
D.6
2.若等腰三角形的两边长是3cm和5cm,则它的周长是(
)
A.11cm
B.13cm
C.11cm或13cm
D.无法确定
3.若等腰三角形的两边长是3cm和6cm,则它的周长是(
)
A.12cm
B.15cm
C.12cm或15cm
D.无法确定
4.若三角形的两边长是3cm和6cm,若第三边为奇数,则它的周长是(
)
A.12cm
B.13cm
14cm
D.15cm
知识点一:三角形的三边关系
变式练习:
1.若三角形三边长为2,4,m,则m的值不可以是(D)
A.3
B.4
C.5
D.6
2.若等腰三角形的两边长是3cm和5cm,则它的周长是(
C
)
A.11cm
B.13cm
C.11cm或13cm
D.无法确定
3.若等腰三角形的两边长是3cm和6cm,则它的周长是(
B
)
A.12cm
B.15cm
C.12cm或15cm
D.无法确定
4.若三角形的两边长是3cm和6cm,若第三边为奇数,则它的周长可能是(
C
)
A.12cm
B.13cm
C.
14cm
D.15cm
知识点二:三角形的内角和定理
三角形的内角和定理:
1.内容:三角形的内角和等于180°.
2.用途:三角形的内角和定理可以计算和证明图形中角的数量关系.
知识点二:三角形的内角和定理
例1:把△ABC沿DE方向剪去∠A后,形成四边形BCED.求证:∠1+∠2=180°+∠A.
知识点二:三角形的内角和定理
例1:把△ABC沿DE方向剪去∠A后,形成四边形BCED.求证:∠1+∠2=180°+∠A.
证明:∵∠1+∠ADE=180°,
∠2+∠AED=180°,
∴∠1=180°-∠ADE,
∠2=180°-∠AED,
∴∠1+∠2=360°-(∠ADE+∠AED),
又∵∠ADE+∠AED=180°-∠A
∴∠1+∠2=360°-(180°-∠A)=180°+∠A
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
2.已知:如图,BD平分∠ABC,CE平分∠ACB,BD与CE交于点I,
求证:∠BIC=90°+
∠A.
知识点三:三角形中的线段
1.三角形的高线:
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,AH⊥BC,垂足为点H,则线段AH是△ABC的BC边上的高.
知识点三:三角形中的线段
2.三角形的角平分线和中线
在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
如图1,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线.
在三角形中,连接一个顶点与它的对边中点的线段叫作三角形的中线.
如图2,BE=EC,则线段AE是△ABC的BC边上的中线.
知识点三:三角形中的线段
例1.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°;
(4)SΔABC=
.
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是中线,
BC-AC=5cm,
∴
ΔDBC的周长比ΔDAC的周长多5cm,
∴
ΔDAC=25cm—5cm=20cm.
知识点三:三角形中的线段
变式练习:
2.在△ABC中,已知AD是角平分线,∠B=50°,∠C=70°,∠BAD=
°.
知识点三:三角形中的线段
变式练习:
2.在△ABC中,已知AD是角平分线,∠B=50°,∠C=70°,∠BAD= 30 °.
知识点三:三角形中的线段
变式练习:
3.如图,△ABC中,
AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
解:∵AD是BC边上的高,∠EAD=5°,
∴∠A
ED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
?
《三角形》复习用课件
知识点一:三角形的三边关系
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边;
知识点一:三角形的三边关系
1.三角形的三边关系:
三角形任何两边的和大于________.
如图所示,若△ABC的三边BC,AC,
AB分别记为a,b,c,则有:a+b>c,a+c>b,b+c>a.
2.二级结论:
(1)三角形任意___________
小于第三边.
(2)三角形的三边关系可表示为:若三角形的两边长为m,
n(m≥n),则第三边长x的取值范围是_______________
.
知识点一:三角形的三边关系
例1.判断下列各组线段中,哪些首尾相接能组成三角形,哪些不能组成三角形,并说明理由.
(1).2,3,5
(2).2,3,6
(3).3,4,5
要判断三条线段能否组成三角形,依据“三角形任
何两边的和
大于第三边”,只要把最长的一条线段
与另外两条线段的和作比较.如果最
长的一条线段
小于另外两条线段的和,那么这三条线段就能组成
三角形;
如果最长的一条线段大于或等于另外两条
线段的和,那么这三条线段就不
能组成三角形.
答案(3)
知识点一:三角形的三边关系
例2.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
根据三角形的三边关系即可求出x的取值范围.
解答:∵三角形的三边长分别为4,7,x,
∴7-4<x<7+4,即3<x<11.∴选A.
知识点一:三角形的三边关系
变式练习:
1.若三角形三边长为2,4,m,则m的值不可以是(
)
A.3
B.4
C.5
D.6
2.若等腰三角形的两边长是3cm和5cm,则它的周长是(
)
A.11cm
B.13cm
C.11cm或13cm
D.无法确定
3.若等腰三角形的两边长是3cm和6cm,则它的周长是(
)
A.12cm
B.15cm
C.12cm或15cm
D.无法确定
4.若三角形的两边长是3cm和6cm,若第三边为奇数,则它的周长是(
)
A.12cm
B.13cm
14cm
D.15cm
知识点一:三角形的三边关系
变式练习:
1.若三角形三边长为2,4,m,则m的值不可以是(D)
A.3
B.4
C.5
D.6
2.若等腰三角形的两边长是3cm和5cm,则它的周长是(
C
)
A.11cm
B.13cm
C.11cm或13cm
D.无法确定
3.若等腰三角形的两边长是3cm和6cm,则它的周长是(
B
)
A.12cm
B.15cm
C.12cm或15cm
D.无法确定
4.若三角形的两边长是3cm和6cm,若第三边为奇数,则它的周长可能是(
C
)
A.12cm
B.13cm
C.
14cm
D.15cm
知识点二:三角形的内角和定理
三角形的内角和定理:
1.内容:三角形的内角和等于180°.
2.用途:三角形的内角和定理可以计算和证明图形中角的数量关系.
知识点二:三角形的内角和定理
例1:把△ABC沿DE方向剪去∠A后,形成四边形BCED.求证:∠1+∠2=180°+∠A.
知识点二:三角形的内角和定理
例1:把△ABC沿DE方向剪去∠A后,形成四边形BCED.求证:∠1+∠2=180°+∠A.
证明:∵∠1+∠ADE=180°,
∠2+∠AED=180°,
∴∠1=180°-∠ADE,
∠2=180°-∠AED,
∴∠1+∠2=360°-(∠ADE+∠AED),
又∵∠ADE+∠AED=180°-∠A
∴∠1+∠2=360°-(180°-∠A)=180°+∠A
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
1.把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为(
)
A.125°B.120°C.140°D.130°
解析:∵EF∥GH,∴∠FCD=∠2,
又∵∠FCD是△ABC的外角,
∴∠FCD=∠1+∠A=130°,
即∠2=130°,选D
知识点二:三角形的内角和定理
变式练习:
2.已知:如图,BD平分∠ABC,CE平分∠ACB,BD与CE交于点I,
求证:∠BIC=90°+
∠A.
知识点三:三角形中的线段
1.三角形的高线:
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线,简称三角形的高.
如图,AH⊥BC,垂足为点H,则线段AH是△ABC的BC边上的高.
知识点三:三角形中的线段
2.三角形的角平分线和中线
在三角形中,一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫作三角形的角平分线.
如图1,∠BAD=∠CAD,则线段AD是△ABC的一条角平分线.
在三角形中,连接一个顶点与它的对边中点的线段叫作三角形的中线.
如图2,BE=EC,则线段AE是△ABC的BC边上的中线.
知识点三:三角形中的线段
例1.如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°;
(4)SΔABC=
.
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
知识点三:三角形中的线段
变式练习:
1.在ΔABC中,CD是中线,已知BC-AC=5cm,
ΔDBC的周长为25cm,求ΔADC的周长.
A
D
B
C
解:∵CD是中线,
BC-AC=5cm,
∴
ΔDBC的周长比ΔDAC的周长多5cm,
∴
ΔDAC=25cm—5cm=20cm.
知识点三:三角形中的线段
变式练习:
2.在△ABC中,已知AD是角平分线,∠B=50°,∠C=70°,∠BAD=
°.
知识点三:三角形中的线段
变式练习:
2.在△ABC中,已知AD是角平分线,∠B=50°,∠C=70°,∠BAD= 30 °.
知识点三:三角形中的线段
变式练习:
3.如图,△ABC中,
AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
解:∵AD是BC边上的高,∠EAD=5°,
∴∠A
ED=85°,
∵∠B=50°,
∴∠BAE=∠AED﹣∠B=85°﹣50°=35°,
∵AE是∠BAC的角平分线,∴∠BAC=2∠BAE=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣50°﹣70°=60°.
?
