人教版数学九年级上册第23章 旋转章节复习课件(共22张)
文档属性
| 名称 | 人教版数学九年级上册第23章 旋转章节复习课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 21:01:13 | ||
图片预览






文档简介
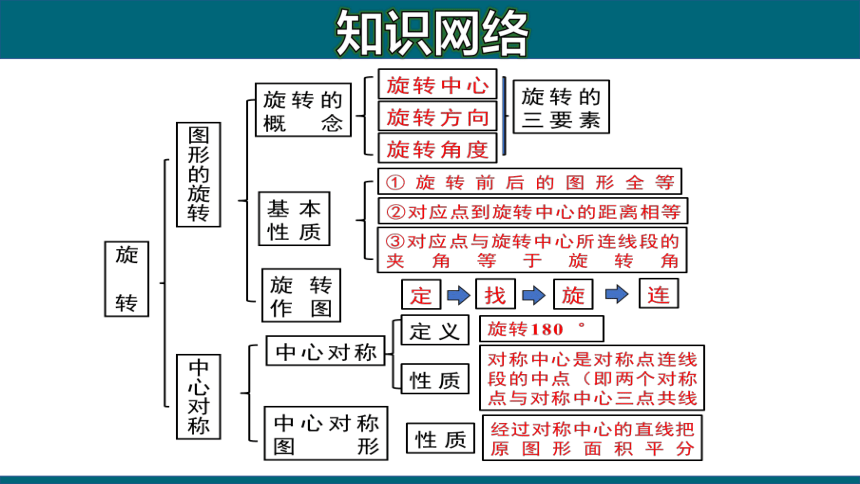
知识网络
一、旋转的特征
1.旋转过程中,图形上______________________按 旋转 .
2.任意一对对应点与旋转中心的连线所成的角都是________,对应点到旋转中心的距离都________.
3.旋转前后对应线段、对应角分别____,图形的大小、形状_________.
每一点都绕旋转中心
同一旋转方向
同样大小的角度
旋转角
相等
相等
不变
知识梳理
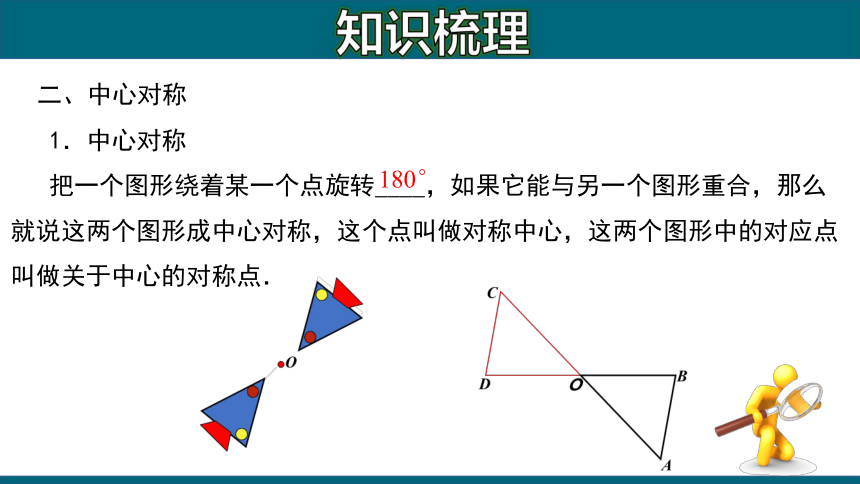
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
二、中心对称
知识梳理
2.中心对称的特征
中心对称的特征:在成中心对称的两个图形中,对应点所连线段都经过___________,并且被对称中心________.
3.中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称中心
平分
知识梳理
横坐标、纵坐标的符号都互为相反数,
三、关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
知识梳理
【例1】(1)如图a,将三角形AOB绕点O按逆时针方向旋转60 °后得到三角形COD,若∠AOB=15 °,则∠AOD的度数是( )
A. 15 ° B. 60 °
C. 45 ° D. 75 °
A
B
O
D
C
图a
C
【解析】关键找出旋转角∠BOD=60 °;
考点解析
旋转的概念及性质的应用
1
(2) 如图b ,4 ×4的正方形网格中, 三角形MNP绕某点旋转一定的角度,得到三角形M1N1P1,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
B
【解析】作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
考点解析
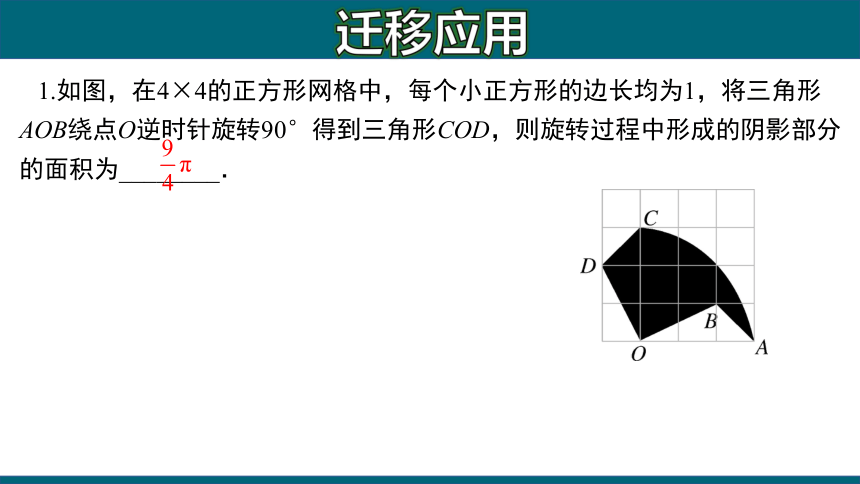
1.如图,在4×4的正方形网格中,每个小正方形的边长均为1,将三角形AOB绕点O逆时针旋转90°得到三角形COD,则旋转过程中形成的阴影部分的面积为________.
迁移应用
2.如图,在正方形网格中,三角形ABC的顶点都在格点(小正方形的顶点)上,将三角形ABC绕点A按逆时针方向旋转90°得到三角形AB1C1.请你作出三角形AB1C1.
【解析】作∠CAC′=90°,且AC=AC′,得到C的对应点C′,由同样的方法得到其余各点的对应点.
解:如图所示:
【点睛】 (1)画旋转后的图形,要善于抓住图形特点,作出特殊点的对应点;(2)旋转作图时要明确三个方面:旋转中心、旋转角度及旋转方向(顺时针或逆时针).
迁移应用
【例2】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【解析】(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
旋转变换
2
考点解析
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
考点解析
3.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 .
A
B
C
D
E
O
4
迁移应用
【例3】如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
考点解析
x
y
O
A
B
A1
B1
A2
B2
【解析】(1)因为旋转角90 °,故用直角三角板及圆规可快速确定对应点的位置;(2)先根据关于原点对称的点的坐标确定对称顶点的坐标,再依次连结得到所要画的图形.
解:(1)如图所示;
(2)如图所示,点A2的坐标为(-3,-2),
B2的坐标为(-1,-3).
考点解析
【例4】如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它把纸片分成面积相等的两部分.
l
考点解析
4.如图,从前一个农民有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间池塘也平分.财主的两个儿子不知怎么做,你能想个办法吗?
解析 先找到平行四边形对角线的交点A,过点A、B两点作一条直线可以了.
A
B
迁移应用
【例5】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
中心对称
3
考点解析
【点睛】中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
5.下列说法不正确的是( )
A.任何一个具有对称中心的四边形都是平行四边形
B.平行四边形既是轴对称图形,又是中心对称图形
C.线段、平行四边形、矩形、菱形、正方形都是中心对称图形
D.正三角形、矩形、菱形、正方形都是轴对称图形,且对称轴都不止一条.
B
迁移应用
【例6】如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法.
m
图形变换的简单应用
4
考点解析
解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是 .
m
考点解析
一、旋转的特征
1.旋转过程中,图形上______________________按 旋转 .
2.任意一对对应点与旋转中心的连线所成的角都是________,对应点到旋转中心的距离都________.
3.旋转前后对应线段、对应角分别____,图形的大小、形状_________.
每一点都绕旋转中心
同一旋转方向
同样大小的角度
旋转角
相等
相等
不变
知识梳理
1.中心对称
把一个图形绕着某一个点旋转____,如果它能与另一个图形重合,那么就说这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
180°
二、中心对称
知识梳理
2.中心对称的特征
中心对称的特征:在成中心对称的两个图形中,对应点所连线段都经过___________,并且被对称中心________.
3.中心对称图形
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
对称中心
平分
知识梳理
横坐标、纵坐标的符号都互为相反数,
三、关于原点对称的点的坐标关系特点
简记为:“关于谁,谁不变,关于原点都改变”.
即:
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
知识梳理
【例1】(1)如图a,将三角形AOB绕点O按逆时针方向旋转60 °后得到三角形COD,若∠AOB=15 °,则∠AOD的度数是( )
A. 15 ° B. 60 °
C. 45 ° D. 75 °
A
B
O
D
C
图a
C
【解析】关键找出旋转角∠BOD=60 °;
考点解析
旋转的概念及性质的应用
1
(2) 如图b ,4 ×4的正方形网格中, 三角形MNP绕某点旋转一定的角度,得到三角形M1N1P1,其旋转中心是( )
A. 点A B. 点B C. 点C D. 点D
B
【解析】作线段MM1与PP1 的垂直平分线,交点便是旋转中心.
考点解析
1.如图,在4×4的正方形网格中,每个小正方形的边长均为1,将三角形AOB绕点O逆时针旋转90°得到三角形COD,则旋转过程中形成的阴影部分的面积为________.
迁移应用
2.如图,在正方形网格中,三角形ABC的顶点都在格点(小正方形的顶点)上,将三角形ABC绕点A按逆时针方向旋转90°得到三角形AB1C1.请你作出三角形AB1C1.
【解析】作∠CAC′=90°,且AC=AC′,得到C的对应点C′,由同样的方法得到其余各点的对应点.
解:如图所示:
【点睛】 (1)画旋转后的图形,要善于抓住图形特点,作出特殊点的对应点;(2)旋转作图时要明确三个方面:旋转中心、旋转角度及旋转方向(顺时针或逆时针).
迁移应用
【例2】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.
【解析】(1)根据题意,找准旋转中心,旋转方向及旋转角度,补全图形即可;
(2)由旋转的性质得∠DCF为直角,由EF与CD平行,得到∠EFC为直角,利用SAS得到△BDC与△EFC全等,利用全等三角形对应角相等即可得证.
旋转变换
2
考点解析
F
解:(1)补全图形,如图所示;
(2)由旋转的性质得,DC=FC,∠DCF=90°,
∴∠DCE+∠ECF=90°.
∵∠ACB=90°,
∴∠DCE+∠BCD=90°,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=180°,
∴∠EFC=90°,
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=90°.
考点解析
3.如图,在等腰Rt△ABC中,点O是AB的中点,AC=4, 将一块边长足够大的三角板的直角顶点放在O点处,将三角板绕点O旋转,始终保持三角板的直角边与AC相交,交点为D,另一条直角边与BC相交,交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 .
A
B
C
D
E
O
4
迁移应用
【例3】如图,在边长为1的正方形组成的网格中,每个正方形的顶点称为格点.已知△AOB的顶点均在格点上,建立如图所示的平面直角坐标系,点A、B的坐标分别是A(3,2) 、B(1,3).
x
y
O
A
B
(1)将△AOB绕点O逆时针旋转90 °后得到△A1OB1,画出旋转后的图形;
(2)画出△AOB关于原点O对称的图形△A2OB2,并写出点A2,B2的坐标.
考点解析
x
y
O
A
B
A1
B1
A2
B2
【解析】(1)因为旋转角90 °,故用直角三角板及圆规可快速确定对应点的位置;(2)先根据关于原点对称的点的坐标确定对称顶点的坐标,再依次连结得到所要画的图形.
解:(1)如图所示;
(2)如图所示,点A2的坐标为(-3,-2),
B2的坐标为(-1,-3).
考点解析
【例4】如图,有一张不规则纸片,若连接EB,则纸片被分为矩形FABE和菱形EBCD,请你用无刻度的直尺画一条直线把这张纸片分成面积相等的两部分,并说明理由.
A
B
C
F
E
D
解: 矩形FABE是中心对称图形,矩形 BCDE也是中心对称图形,所以经过它们中心的直线把图形分成全等的两部分,面积相等.如图直线l既经过矩形FABE的中心,又经过菱形BCDE的中心,所以它把纸片分成面积相等的两部分.
l
考点解析
4.如图,从前一个农民有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间池塘也平分.财主的两个儿子不知怎么做,你能想个办法吗?
解析 先找到平行四边形对角线的交点A,过点A、B两点作一条直线可以了.
A
B
迁移应用
【例5】下列图形中,既是轴对称图形,又是中心对称图形的是( )
A B C D
D
【解析】 图A.图B都是轴对称图形,图C是中心对称图形,图D既是中心对称图形也是轴对称图形.
中心对称
3
考点解析
【点睛】中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另一个是沿一条直线对折.这是易错点,也是辨别它们不同的关键.
5.下列说法不正确的是( )
A.任何一个具有对称中心的四边形都是平行四边形
B.平行四边形既是轴对称图形,又是中心对称图形
C.线段、平行四边形、矩形、菱形、正方形都是中心对称图形
D.正三角形、矩形、菱形、正方形都是轴对称图形,且对称轴都不止一条.
B
迁移应用
【例6】如图所示的图案是一个轴对称图形(不考虑颜色),直线m是它的一条对称轴.已知图中圆的半径为r,求你能借助轴对称的方法求出图中阴影部分的面积吗?说说你的做法.
m
图形变换的简单应用
4
考点解析
解:以直线m为对称轴,把m左边绿色部分反射到m的右边,那么它们的像恰好填补了右边的白色部分,所以图中的绿色部分面积等于半个圆的面积,也就是 .
m
考点解析
同课章节目录
