人教版数学九年级上册24.3 正多边形和圆课件(共24张)
文档属性
| 名称 | 人教版数学九年级上册24.3 正多边形和圆课件(共24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 21:17:30 | ||
图片预览




文档简介
学习目标
了解正多边形和圆的有关概念.
理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
会应用正多边形和圆的有关知识解决实际问题.
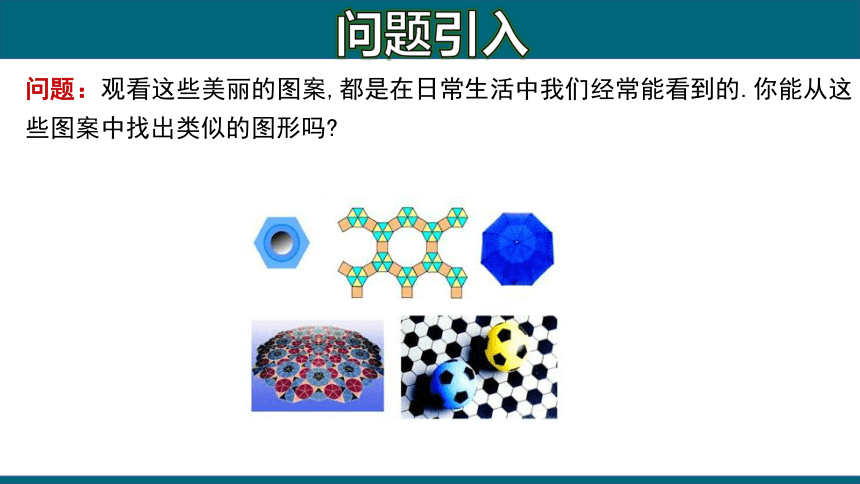
问题:观看这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
问题引入
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
知识精讲
强调
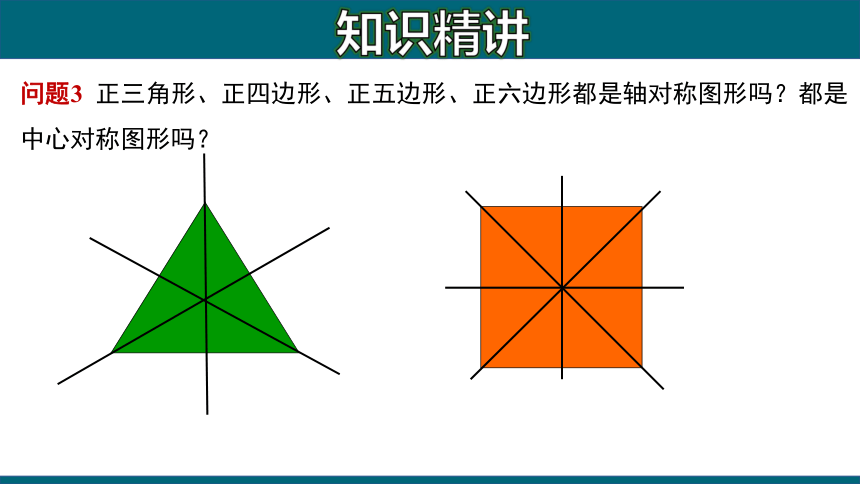
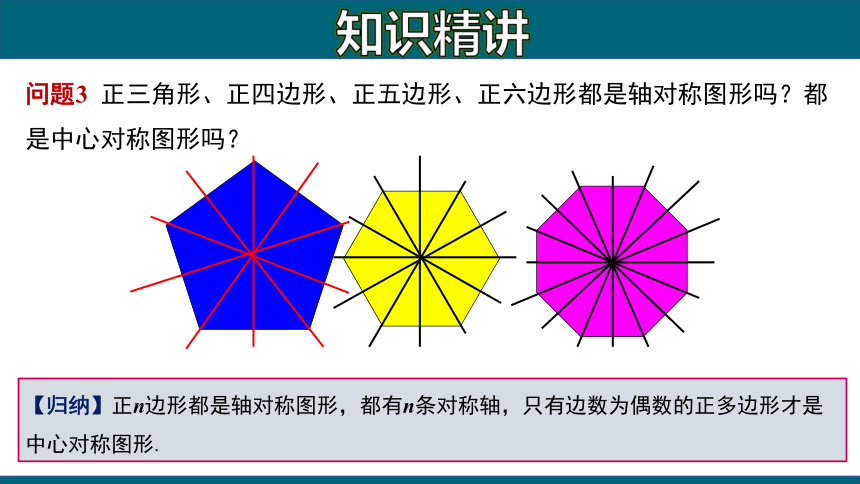
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
知识精讲
【归纳】正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
问题1
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
知识精讲
O
A
B
C
D
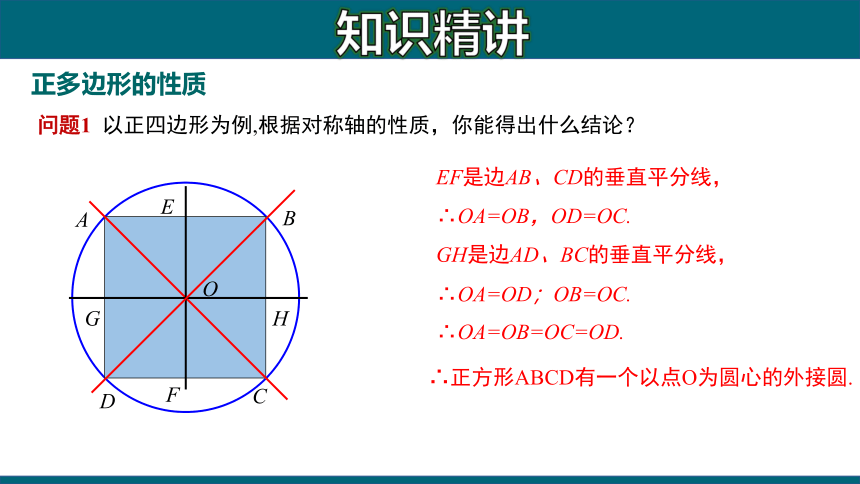
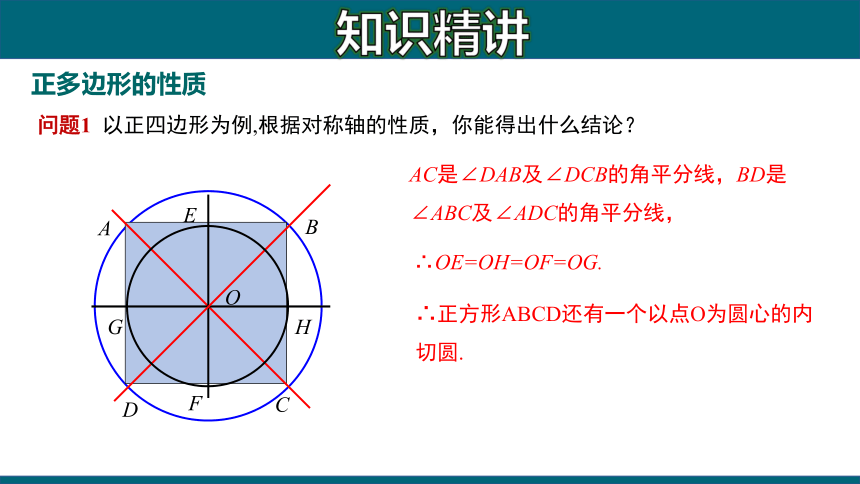
问题1 以正四边形为例,根据对称轴的性质,你能得出什么结论?
E
F
G
H
EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD、BC的垂直平分线,
∴OA=OD;OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
正多边形的性质
知识精讲
O
A
B
C
D
E
F
G
H
AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
问题1 以正四边形为例,根据对称轴的性质,你能得出什么结论?
正多边形的性质
知识精讲
所有的正多边形是不是也都有一个外接圆和一个内切圆?
任何正多边形都有一个外接圆和一个内切圆.
想一想
知识精讲
O
A
B
C
D
E
F
G
H
R
r
正多边形的外接圆和内切圆的公共圆心,叫作正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
知识要点
正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于
知识精讲
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0} 正多边
形边数
内角
中心角
外角
3
4
6
n
60 °
120 °
120 °
90 °
90 °
90 °
120 °
60 °
60 °
正多边形的外角=中心角
练一练
完成下面的表格:
针对练习
如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度 ;
② OC BC (填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是
△OBC面积的 倍.
⑤圆内接正n边形面积公式:_______________________.
60
=
等边
6
正多边形的有关计算
知识精讲
问题1 正n边形的中心角怎么计算?
问题2 正n边形的边长a,半径R,边心距r之间有什么关系?
问题3 边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
正多边形的有关计算
知识精讲
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
C
M
中心角一半
知识精讲
例1:有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
抽象成
典例解析
B
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OMB中,OB=4, MB=
4m
O
A
B
C
D
E
F
M
r
解:过点O作OM⊥BC于M.
典例解析
∴BC=2MB=4,周长为4×6=24m
正多边形边数
半径
边长
边心距
周长
面积
3
4
1
6
1. 填表
2
1
2
8
4
2
2
12
2. 若正多边形的边心距与半径的比为1:2,则这个多边形的边数是 .
3
达标检测
3.如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是 ( )
A.60° B.45° C. 36° D. 30°
·
A
B
C
D
E
O
C
达标检测
5. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要 cm.
4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为 度.(不取近似值)
达标检测
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
解:∵正方形的面积等于4,
则半径为
∴⊙O的面积为
∴正方形的边长AB=2.
达标检测
A
B
C
D
E
F
P
7.如图,正六边形ABCDEF的边长为 ,点P为六边形内任一点.则点P到各边距离之和是多少?
∴点P到各边距离之和=3BD=3×6=18.
解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G.
G
H
K
∴P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形
∴AB∥DE,AF∥CD,BC∥EF,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,BD∥HK,且BD=HK.
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=6.
达标检测
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON= ;
图③中∠MON= ;
(2)试探究∠MON的度数与正n边形的边数n的关系.
A
B
C
D
E
A
B
C
D
.
A
B
C
M
N
M
N
M
N
O
O
O
90 °
72 °
120 °
图①
图②
图③
达标检测
小结梳理
了解正多边形和圆的有关概念.
理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
会应用正多边形和圆的有关知识解决实际问题.
问题:观看这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
问题引入
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
正多边形
各边相等
各角相等
缺一不可
知识精讲
强调
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
知识精讲
【归纳】正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
问题1
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
知识精讲
O
A
B
C
D
问题1 以正四边形为例,根据对称轴的性质,你能得出什么结论?
E
F
G
H
EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.
GH是边AD、BC的垂直平分线,
∴OA=OD;OB=OC.
∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
正多边形的性质
知识精讲
O
A
B
C
D
E
F
G
H
AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
问题1 以正四边形为例,根据对称轴的性质,你能得出什么结论?
正多边形的性质
知识精讲
所有的正多边形是不是也都有一个外接圆和一个内切圆?
任何正多边形都有一个外接圆和一个内切圆.
想一想
知识精讲
O
A
B
C
D
E
F
G
H
R
r
正多边形的外接圆和内切圆的公共圆心,叫作正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
知识要点
正多边形每一条边所对的圆心角,叫做正多边形的中心角.正多边形的每个中心角都等于
知识精讲
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0} 正多边
形边数
内角
中心角
外角
3
4
6
n
60 °
120 °
120 °
90 °
90 °
90 °
120 °
60 °
60 °
正多边形的外角=中心角
练一练
完成下面的表格:
针对练习
如图,已知半径为4的圆内接正六边形ABCDEF:
①它的中心角等于 度 ;
② OC BC (填>、<或=);
③△OBC是 三角形;
④圆内接正六边形的面积是
△OBC面积的 倍.
⑤圆内接正n边形面积公式:_______________________.
60
=
等边
6
正多边形的有关计算
知识精讲
问题1 正n边形的中心角怎么计算?
问题2 正n边形的边长a,半径R,边心距r之间有什么关系?
问题3 边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
正多边形的有关计算
知识精讲
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
O
边心距r
边长一半
半径R
C
M
中心角一半
知识精讲
例1:有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
抽象成
典例解析
B
利用勾股定理,可得边心距
亭子地基的面积
在Rt△OMB中,OB=4, MB=
4m
O
A
B
C
D
E
F
M
r
解:过点O作OM⊥BC于M.
典例解析
∴BC=2MB=4,周长为4×6=24m
正多边形边数
半径
边长
边心距
周长
面积
3
4
1
6
1. 填表
2
1
2
8
4
2
2
12
2. 若正多边形的边心距与半径的比为1:2,则这个多边形的边数是 .
3
达标检测
3.如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是 ( )
A.60° B.45° C. 36° D. 30°
·
A
B
C
D
E
O
C
达标检测
5. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要 cm.
4.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为 度.(不取近似值)
达标检测
6.如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
解:∵正方形的面积等于4,
则半径为
∴⊙O的面积为
∴正方形的边长AB=2.
达标检测
A
B
C
D
E
F
P
7.如图,正六边形ABCDEF的边长为 ,点P为六边形内任一点.则点P到各边距离之和是多少?
∴点P到各边距离之和=3BD=3×6=18.
解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G.
G
H
K
∴P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形
∴AB∥DE,AF∥CD,BC∥EF,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,BD∥HK,且BD=HK.
∵CG⊥BD,
∴BD=2BG=2×BC×cos∠CBD=6.
达标检测
8.如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON=_______;图②中∠MON= ;
图③中∠MON= ;
(2)试探究∠MON的度数与正n边形的边数n的关系.
A
B
C
D
E
A
B
C
D
.
A
B
C
M
N
M
N
M
N
O
O
O
90 °
72 °
120 °
图①
图②
图③
达标检测
小结梳理
同课章节目录
