人教版数学九年级上册25.2.1 运用直接列举或列表法求概率课件(共24张)
文档属性
| 名称 | 人教版数学九年级上册25.2.1 运用直接列举或列表法求概率课件(共24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-27 21:29:03 | ||
图片预览







文档简介
学习目标
知道什么时候采用“直接列举法”和“列表法” .
会正确“列表”表示出所有可能出现的结果.
知道如何利用“列表法”求随机事件的概率.
我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.
情景引入
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
知识精讲
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
知识精讲
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
知识精讲
解:
(1)两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形;所以学生赢的概率是
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形;所以老师赢的概率是
∵P(学生赢)=P(老师赢).
∴这个游戏是公平的.
知识精讲
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
知识精讲
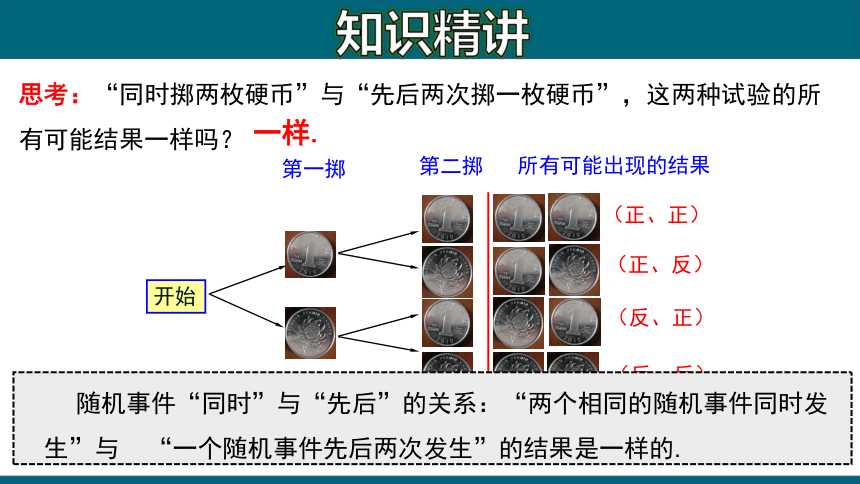
思考:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样.
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
知识精讲
问题1 同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
还有别的方法求下列事件的概率吗?
方法一:直接列举法
知识精讲
①
①
①
②
②
①
①
②
②
②
①
②
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
还可以用列表法求概率
知识精讲
问题2 怎样列表格?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
知识精讲
例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
典例解析
{5940675A-B579-460E-94D1-54222C63F5DA}
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
典例解析
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
典例解析
例2 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
典例解析
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
典例解析
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
变式练习
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
达标检测
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
达标检测
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)=
达标检测
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
第
一
张
第
二
张
达标检测
解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =
小结梳理
知道什么时候采用“直接列举法”和“列表法” .
会正确“列表”表示出所有可能出现的结果.
知道如何利用“列表法”求随机事件的概率.
我们在日常生活中经常会做一些游戏,游戏规则制定是否公平,对游戏者来说非常重要,其实这是一个游戏双方获胜概率大小的问题.
情景引入
老师向空中抛掷两枚同样的一元硬币,如果落地后一正一反,老师赢;如果落地后两面一样,你们赢.请问,你们觉得这个游戏公平吗?
我们一起来做游戏
知识精讲
同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
①
②
知识精讲
“掷两枚硬币”所有结果如下:
正正
正反
反正
反反
①
②
①
②
①
②
①
②
知识精讲
解:
(1)两枚硬币两面一样包括两面都是正面,两面都是反面,共两种情形;所以学生赢的概率是
(2)一枚硬币正面朝上,一枚硬币反面朝上,共有反正,正反两种情形;所以老师赢的概率是
∵P(学生赢)=P(老师赢).
∴这个游戏是公平的.
知识精讲
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
【适用范围】直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
知识精讲
思考:“同时掷两枚硬币”与“先后两次掷一枚硬币”,这两种试验的所有可能结果一样吗?
开始
第一掷
第二掷
所有可能出现的结果
(正、正)
(正、反)
(反、正)
(反、反)
一样.
随机事件“同时”与“先后”的关系:“两个相同的随机事件同时发生”与 “一个随机事件先后两次发生”的结果是一样的.
知识精讲
问题1 同时掷两枚硬币,试求下列事件的概率:
(1)两枚两面一样;
(2)一枚硬币正面朝上,一枚硬币反面朝上;
还有别的方法求下列事件的概率吗?
方法一:直接列举法
知识精讲
①
①
①
②
②
①
①
②
②
②
①
②
第1枚硬币
第
2
枚硬币
反
正
正
反
正
正
反
正
正
反
反
反
还可以用列表法求概率
知识精讲
问题2 怎样列表格?
一个因素所包含的可能情况
另一个因素所包含的可能情况
两个因素所组合的所有可能情况,即n
列表法中表格构造特点:
说明:如果第一个因素包含2种情况;第二个因素包含3种情况;那么所有情况n=2×3=6.
知识精讲
例1 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
典例解析
{5940675A-B579-460E-94D1-54222C63F5DA}
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
典例解析
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
典例解析
例2 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
典例解析
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
典例解析
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
变式练习
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
达标检测
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
达标检测
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)=
达标检测
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
第
一
张
第
二
张
达标检测
解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =
小结梳理
同课章节目录
