七年级上册数学人教版1.5.2科学计数法课件(26张ppt)
文档属性
| 名称 | 七年级上册数学人教版1.5.2科学计数法课件(26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-30 00:00:00 | ||
图片预览







文档简介
知识回顾
3、式子 表示的意义是_________。
2、 在 中,a叫做____,n叫做____,
底数
指数
幂
n个a相乘
4. (-4)8 __ 0 (-4)9__ 0
>
<
1、什么运算叫乘方?什么叫幂?
求几个相同因数积的运算叫做乘方.
乘方的结果叫做
生活中的一些数字
北京故宫的占地面积约为721 000m?.
生活中,我们经常会接触一些较大的数,
生活中的一些数字
2008年北京奥运会体育场——“鸟巢”能容纳91 000位观众。
生活中的一些数字
第六次人口普查时,中国人口约为:
1,370,000,000人
可见:
象这样较大的数据,书写和阅读都有一定困难,那么有没有一种表示方法,使得这些大数易写,易读,易计算呢?
太阳的半径为 696 000 000千米;
光的速度为 300 000 000 米/秒;
“鸟巢”能容纳91 000位观众。.
… …
我国人口已达1 370 000 000人;
这就是本节课我们要学习的内容——科学记数法.
1、能用科学记数法表示较大数。(重点)
2、能将用科学记数法表示的数还原成原数。(重点)
3、科学记数法在实际生活中的应用。
学习目标
你知道 分别等于多少吗? 的意义和规律是什么?
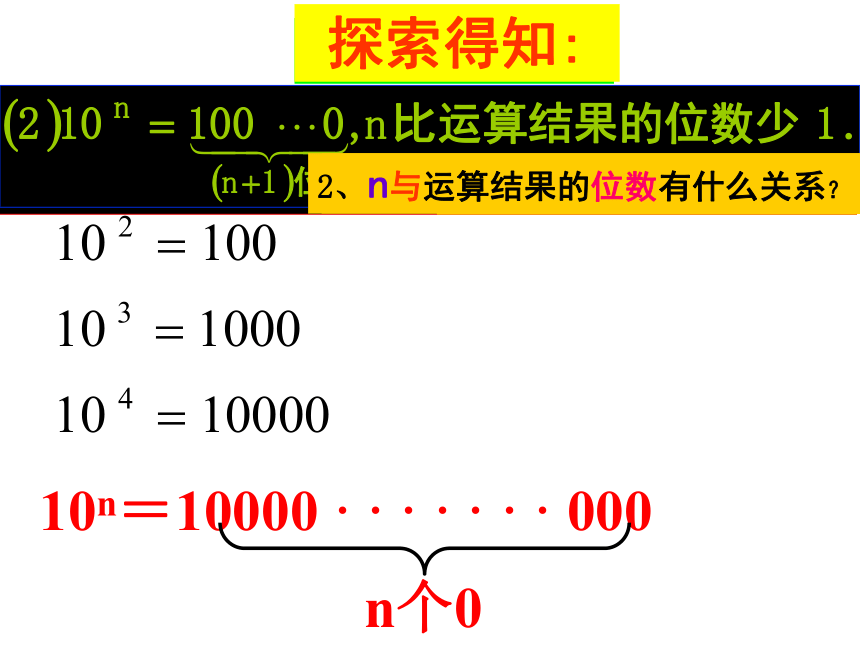
10n=10000 · · · · · · · 000
n个0
研究10n的特征
探索得知:
10n中的n表示n个10相乘
1、n与运算结果中0的个数有什么关系?
2、n与运算结果的位数有什么关系?
试一试:
1.把下列各数写成10的幂的形式.
(1)10 000
(2)10 000 000
(3)100 000 000
2.指出下列各数原数是几位数.
(1)102 (2)104 (3)1021 (4)10100
=104
=107
=108
3位数
22位数
101位数
5位数
① n=原数的整数位数-1 (或者)
在1的后面有几个0,n就是几。
② 原数的整数位数=n的次数+1。
100=10×10=__; 1000=___;
10000=__; 100000=__。
观察思考:把100……0这样的数,写成10n的形式有什么规律?
总结发现:在1的后面有几个0,n就是几。
所以,我们就猜想能不能用10的乘方的形式也来表示一些大数呢?
102
103
104
105
如:3.5×10 00000=35 00000=3.5×106
(把下列数写成幂的形式.)
在小学里我们学过的关于小数点移动的知识,通过移动小数点位置可以把一个大数表示成整数部分的位数是一位的数乘以10的n次幂的形式.这样呀大数就变得读、写都简单了。
(1) 6 100 000 000
6100000000
6100000000 = 6.1 × 109
小数点原来的位置
小数点最后的位置
小数点向左移了9次
注意: 6.1是原数保留一位整数得来的
n=原数的整数位数-1
讨论、点拨、更正
任何一个数都可以表示成整数部分的位数是一位的数乘以10的n次幂的形式.
= 6.1× 1 000 000 000
= 6.1× 109
方法:先将小数点向左移动n位后,去0,再补
234500.82
小数点最后的位置
小数点向左移了5次
小数点原来的位置
2.3450082X105
234500.82=
(2) 234500.82
= 2.3450082× 100 000
= 2.3450082× 105
讨论、点拨、更正
任何一个数都可以表示成整数部分的位数是一位的数乘以10的n次幂的形式.
思考:你会借用乘方的形式表示下面的大数吗?
1 370 000 000 可表示成_____________
64 00 000 可表示成__________
300 000 000 可表示成__________
1.37×109
6.4×106
3×108
一般形式: a×10n
把一个大数表示成a×10n的形式,大数就变得简单了,那么a和n如何确定呢?
a表示:整数位数只有一位的数。
指数n表示:正整数。
一、定义(概念):
像上面这样,把一个大于10 的数表示成整数位数只有一位的数×10n的形式,这种记数的方法称为科学记数法。
(其中整数位数只有一位的数用字母a表示,指数用字母n表示)
科学记数法
简记为:
a×10n
(1)1≤|a|<10
(2) n是正整数
5 6 7 0 0 0 0 0 0 =5.67×
-7 0 0 0 0 = -7×
像这样,把一个大于10的数可以表示成 a×10n的形式,
a是整数数位只有一位的数,即1≤|a|<10.
其中n是正整数,
科学记数法:
.
.
.
.
小数点向左移动8位,
小数点向左移动4位,
去0,
去0,
补
再补
方法:先将小数点向左移动n位后,去0,再补
结论:科学记数法中的n就是原数变为a时小数点向左移动的位数。
例题:
用科学记数法表示下列各数:
(1)1 000 000;(2)57 000 000;
(3)123 000 000 000
解(1)1000000=
106
(2)57000000=
5.7 × 10 000 000=
(3)123 000 000 000
=1.23 × 100 000 000 000
=1.23 × 1011
观察与思考:
1、上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
2、用科学记数法表示一个m位整数,其中10的指数是 。
m-1
5.7 × 107
即n=m-1
关键:①a的确定1≤a<10 ;②n的确定n=m-1
科学记数法
将下列数值写成科学记数法 a × 10n 。
100 000 = 105
10 000 = 104
1 000 = 103
100 = 102
10 = 101
(a) 400 000
= 4 × 100 000
= 4 × 105
400 000
= 40 × 10 000
= 40 × 104
此答案有何问题?
此数不可大于或等于10!
此数亦不可小于1!
n 是整数
1 ? a? 10
1000 000
= 10
6
57 000 000
= 5.7×10
7
123 000 000 000
=1.23×10
11
思考:
下面的式子中, 等号右边10的指数和等号左边整数的位数,它们存在什么关系?
a×10n 中10的指数n=整数的位数-1.
用科学记数法表示一个n位整数的数,那10的指数应是_________.
n-1
试一试:
如果一个数有9位整数,那10的指数是_______.
8
下面信息中的大数已经用科学记数法表示了,你知道原数是谁吗?
练一练:
(2)某市去年总共缺水6.2×10 吨;
原数是____________________吨,
6
(1)一口痰大约含有细菌1.3×10 个;
原数是___________________个,
8
(3)据中国电监会统计,我国今年预计将缺电6×10 千瓦时;
原数是___________________千瓦时,
130 000 000
6 200 000
60 000 000 000
(4) -2.4×10 =________________.
4
-24000
把用科学记数法表示的a×10 形式的数还原成原数时,则整数部分的位数为n+1。
是___位数
是___位数
是___位数
是___位数
9
7
11
5
n
10
在下列各大数的表示方法中,是科学记数法的是( )
C、-9 976 000=-99.76×105
D、10 000 000=10×106
此数不能小于1
B、45 000 000=0.45×108
此数也不能大于或等于10
A、5 629 000=5.629×106
此数的绝对值只能小于10
在以下的各数中,最大的数为( )
(A)7.2 × (B)2.5×
(C)9.9 × (D)1×
在下列各数中最小的为( )
(A)3.14 × (B)3.1×
(C)3.2× (D)3.142×
比较大小
中国森林面积约为1.2863×108公顷
解:1.2863×108=128 630 000公顷
原来的数是多少呢?
据测算,我国每天因土地沙漠化造成
的经济损失为1.5亿元,按一年365天计算,
我国一年因土地沙漠化造成的经济损失是
多少元?(用科学记数法表示)
解:150000000×365
=54750000000
=5.475×1010(元)
答:我国一年因土地沙漠化造成的经济损失是5.475×1010元。
我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水。据测试,没拧紧的水龙头每秒钟会滴下2滴水,每滴水约 0.05毫升。小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴了多少毫升水.(结果用科学记数法表示)
解:
2×0.05×60×60×4
=1.44×103(毫升)
答:水龙头滴了1.44×103毫升水。
=1440
1. 科学记数法如何来表示?
(3)第三招:通过小数点的移动得到原数(
).
一般形式:a×10n(1≤|a|<10,n为正整数)
2.三招学好科学记数法.
(2)第二招:弄清n与原数的整数位数的关系(
);
整数的位数
为n+1次
(1)第一招:牢记a的取值范围( );
1≤|a|<10
a的小数点向右移动n位
a是原数保留一位整数得来的
n=原数的整数位数-1
3. 科学记数法的还原。
① 根据a×10n 中10的指数n来确定, n是几,就将小数点向右移动几位,把10n去掉即可。
② 原数的整数位数=n的次数+1。
1.生活中的数学小常识:
百: 千: 万:
百万: 亿:
2.用科学记数法表示3.14× 的整数位有( )
B、n位
D、(n+2)位
C、(n+1)位
A、(n-1)位
C
3.水星与太阳的平均距离约为57 900 000千米.
______________;
5.79×10
7
3、式子 表示的意义是_________。
2、 在 中,a叫做____,n叫做____,
底数
指数
幂
n个a相乘
4. (-4)8 __ 0 (-4)9__ 0
>
<
1、什么运算叫乘方?什么叫幂?
求几个相同因数积的运算叫做乘方.
乘方的结果叫做
生活中的一些数字
北京故宫的占地面积约为721 000m?.
生活中,我们经常会接触一些较大的数,
生活中的一些数字
2008年北京奥运会体育场——“鸟巢”能容纳91 000位观众。
生活中的一些数字
第六次人口普查时,中国人口约为:
1,370,000,000人
可见:
象这样较大的数据,书写和阅读都有一定困难,那么有没有一种表示方法,使得这些大数易写,易读,易计算呢?
太阳的半径为 696 000 000千米;
光的速度为 300 000 000 米/秒;
“鸟巢”能容纳91 000位观众。.
… …
我国人口已达1 370 000 000人;
这就是本节课我们要学习的内容——科学记数法.
1、能用科学记数法表示较大数。(重点)
2、能将用科学记数法表示的数还原成原数。(重点)
3、科学记数法在实际生活中的应用。
学习目标
你知道 分别等于多少吗? 的意义和规律是什么?
10n=10000 · · · · · · · 000
n个0
研究10n的特征
探索得知:
10n中的n表示n个10相乘
1、n与运算结果中0的个数有什么关系?
2、n与运算结果的位数有什么关系?
试一试:
1.把下列各数写成10的幂的形式.
(1)10 000
(2)10 000 000
(3)100 000 000
2.指出下列各数原数是几位数.
(1)102 (2)104 (3)1021 (4)10100
=104
=107
=108
3位数
22位数
101位数
5位数
① n=原数的整数位数-1 (或者)
在1的后面有几个0,n就是几。
② 原数的整数位数=n的次数+1。
100=10×10=__; 1000=___;
10000=__; 100000=__。
观察思考:把100……0这样的数,写成10n的形式有什么规律?
总结发现:在1的后面有几个0,n就是几。
所以,我们就猜想能不能用10的乘方的形式也来表示一些大数呢?
102
103
104
105
如:3.5×10 00000=35 00000=3.5×106
(把下列数写成幂的形式.)
在小学里我们学过的关于小数点移动的知识,通过移动小数点位置可以把一个大数表示成整数部分的位数是一位的数乘以10的n次幂的形式.这样呀大数就变得读、写都简单了。
(1) 6 100 000 000
6100000000
6100000000 = 6.1 × 109
小数点原来的位置
小数点最后的位置
小数点向左移了9次
注意: 6.1是原数保留一位整数得来的
n=原数的整数位数-1
讨论、点拨、更正
任何一个数都可以表示成整数部分的位数是一位的数乘以10的n次幂的形式.
= 6.1× 1 000 000 000
= 6.1× 109
方法:先将小数点向左移动n位后,去0,再补
234500.82
小数点最后的位置
小数点向左移了5次
小数点原来的位置
2.3450082X105
234500.82=
(2) 234500.82
= 2.3450082× 100 000
= 2.3450082× 105
讨论、点拨、更正
任何一个数都可以表示成整数部分的位数是一位的数乘以10的n次幂的形式.
思考:你会借用乘方的形式表示下面的大数吗?
1 370 000 000 可表示成_____________
64 00 000 可表示成__________
300 000 000 可表示成__________
1.37×109
6.4×106
3×108
一般形式: a×10n
把一个大数表示成a×10n的形式,大数就变得简单了,那么a和n如何确定呢?
a表示:整数位数只有一位的数。
指数n表示:正整数。
一、定义(概念):
像上面这样,把一个大于10 的数表示成整数位数只有一位的数×10n的形式,这种记数的方法称为科学记数法。
(其中整数位数只有一位的数用字母a表示,指数用字母n表示)
科学记数法
简记为:
a×10n
(1)1≤|a|<10
(2) n是正整数
5 6 7 0 0 0 0 0 0 =5.67×
-7 0 0 0 0 = -7×
像这样,把一个大于10的数可以表示成 a×10n的形式,
a是整数数位只有一位的数,即1≤|a|<10.
其中n是正整数,
科学记数法:
.
.
.
.
小数点向左移动8位,
小数点向左移动4位,
去0,
去0,
补
再补
方法:先将小数点向左移动n位后,去0,再补
结论:科学记数法中的n就是原数变为a时小数点向左移动的位数。
例题:
用科学记数法表示下列各数:
(1)1 000 000;(2)57 000 000;
(3)123 000 000 000
解(1)1000000=
106
(2)57000000=
5.7 × 10 000 000=
(3)123 000 000 000
=1.23 × 100 000 000 000
=1.23 × 1011
观察与思考:
1、上面的式子中,等号左边整数的位数与右边10的指数有什么关系?
2、用科学记数法表示一个m位整数,其中10的指数是 。
m-1
5.7 × 107
即n=m-1
关键:①a的确定1≤a<10 ;②n的确定n=m-1
科学记数法
将下列数值写成科学记数法 a × 10n 。
100 000 = 105
10 000 = 104
1 000 = 103
100 = 102
10 = 101
(a) 400 000
= 4 × 100 000
= 4 × 105
400 000
= 40 × 10 000
= 40 × 104
此答案有何问题?
此数不可大于或等于10!
此数亦不可小于1!
n 是整数
1 ? a? 10
1000 000
= 10
6
57 000 000
= 5.7×10
7
123 000 000 000
=1.23×10
11
思考:
下面的式子中, 等号右边10的指数和等号左边整数的位数,它们存在什么关系?
a×10n 中10的指数n=整数的位数-1.
用科学记数法表示一个n位整数的数,那10的指数应是_________.
n-1
试一试:
如果一个数有9位整数,那10的指数是_______.
8
下面信息中的大数已经用科学记数法表示了,你知道原数是谁吗?
练一练:
(2)某市去年总共缺水6.2×10 吨;
原数是____________________吨,
6
(1)一口痰大约含有细菌1.3×10 个;
原数是___________________个,
8
(3)据中国电监会统计,我国今年预计将缺电6×10 千瓦时;
原数是___________________千瓦时,
130 000 000
6 200 000
60 000 000 000
(4) -2.4×10 =________________.
4
-24000
把用科学记数法表示的a×10 形式的数还原成原数时,则整数部分的位数为n+1。
是___位数
是___位数
是___位数
是___位数
9
7
11
5
n
10
在下列各大数的表示方法中,是科学记数法的是( )
C、-9 976 000=-99.76×105
D、10 000 000=10×106
此数不能小于1
B、45 000 000=0.45×108
此数也不能大于或等于10
A、5 629 000=5.629×106
此数的绝对值只能小于10
在以下的各数中,最大的数为( )
(A)7.2 × (B)2.5×
(C)9.9 × (D)1×
在下列各数中最小的为( )
(A)3.14 × (B)3.1×
(C)3.2× (D)3.142×
比较大小
中国森林面积约为1.2863×108公顷
解:1.2863×108=128 630 000公顷
原来的数是多少呢?
据测算,我国每天因土地沙漠化造成
的经济损失为1.5亿元,按一年365天计算,
我国一年因土地沙漠化造成的经济损失是
多少元?(用科学记数法表示)
解:150000000×365
=54750000000
=5.475×1010(元)
答:我国一年因土地沙漠化造成的经济损失是5.475×1010元。
我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水。据测试,没拧紧的水龙头每秒钟会滴下2滴水,每滴水约 0.05毫升。小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后水龙头滴了多少毫升水.(结果用科学记数法表示)
解:
2×0.05×60×60×4
=1.44×103(毫升)
答:水龙头滴了1.44×103毫升水。
=1440
1. 科学记数法如何来表示?
(3)第三招:通过小数点的移动得到原数(
).
一般形式:a×10n(1≤|a|<10,n为正整数)
2.三招学好科学记数法.
(2)第二招:弄清n与原数的整数位数的关系(
);
整数的位数
为n+1次
(1)第一招:牢记a的取值范围( );
1≤|a|<10
a的小数点向右移动n位
a是原数保留一位整数得来的
n=原数的整数位数-1
3. 科学记数法的还原。
① 根据a×10n 中10的指数n来确定, n是几,就将小数点向右移动几位,把10n去掉即可。
② 原数的整数位数=n的次数+1。
1.生活中的数学小常识:
百: 千: 万:
百万: 亿:
2.用科学记数法表示3.14× 的整数位有( )
B、n位
D、(n+2)位
C、(n+1)位
A、(n-1)位
C
3.水星与太阳的平均距离约为57 900 000千米.
______________;
5.79×10
7
