人教版数学七年级上册:1.3.2有理数的减法 课件(28张ppt)
文档属性
| 名称 | 人教版数学七年级上册:1.3.2有理数的减法 课件(28张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 969.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-28 08:46:20 | ||
图片预览



文档简介
1.3.2 有理数的减法
有理数的减法
1.3.2
1、理解并掌握有理数的减法法则,能进行有理数的减法运算。
2、能正确完成减法到加法的转化,培养自身的观察能力和思维能力
异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
一个数与0相加,仍得这个数.
(1) ( +4) + (+16) =
(2)(–2)+(–27)=
(3)(–9)+ 10 =
(4) 45 +(–60)=
(5)(–7)+ 7 =
(6) 16 + 0 =
(7) 0 + (–8) =
20
–29
1
–15
16
–8
同号两数相加,取与加数相同的符号,并把绝对值相加.
0
互为相反数的两个数相加得0.
温故而知新
0
1
2
3
-1
-2
-3
-4
4
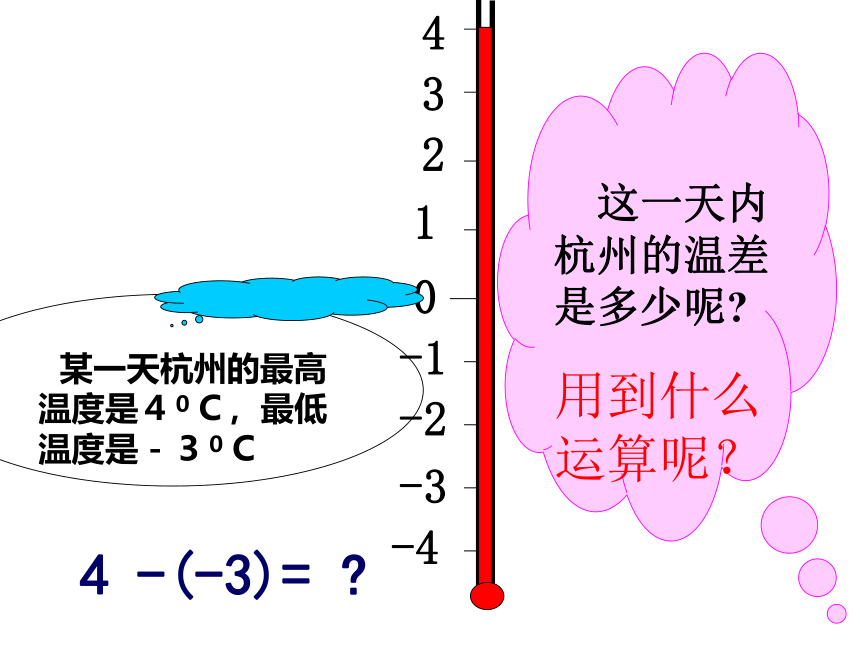
这一天内杭州的温差是多少呢?
某一天杭州的最高温度是40C,最低温度是-30C
用到什么运算呢?
4 -(-3)= ?
0
1
2
3
-1
-2
-3
-4
4
0
1
2
3
-1
-2
-3
-4
4
0
1
2
3
-1
-2
-3
-4
4
4
3
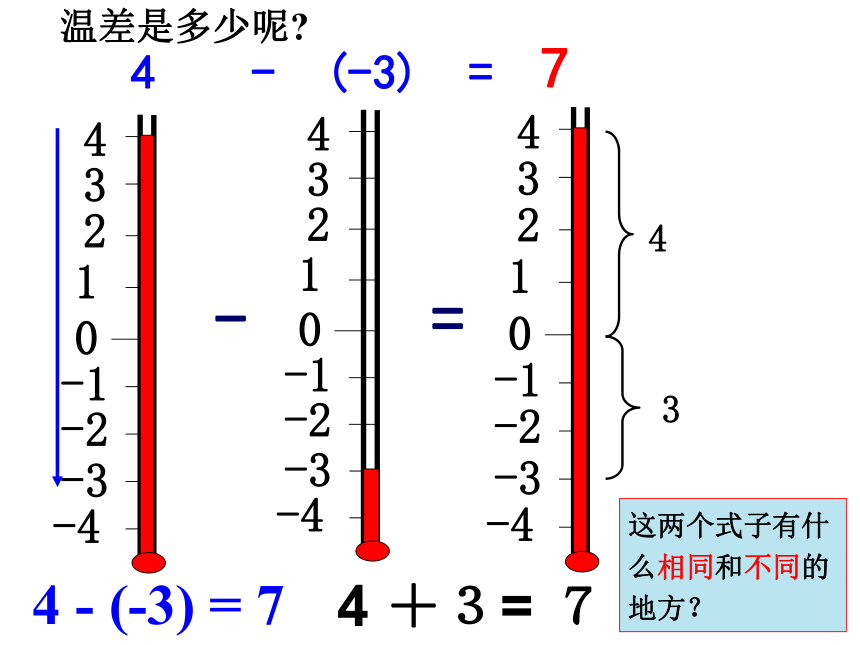
4 +3= 7
4 - (-3) = ?
7
-
=
温差是多少呢?
4 - (-3) = 7
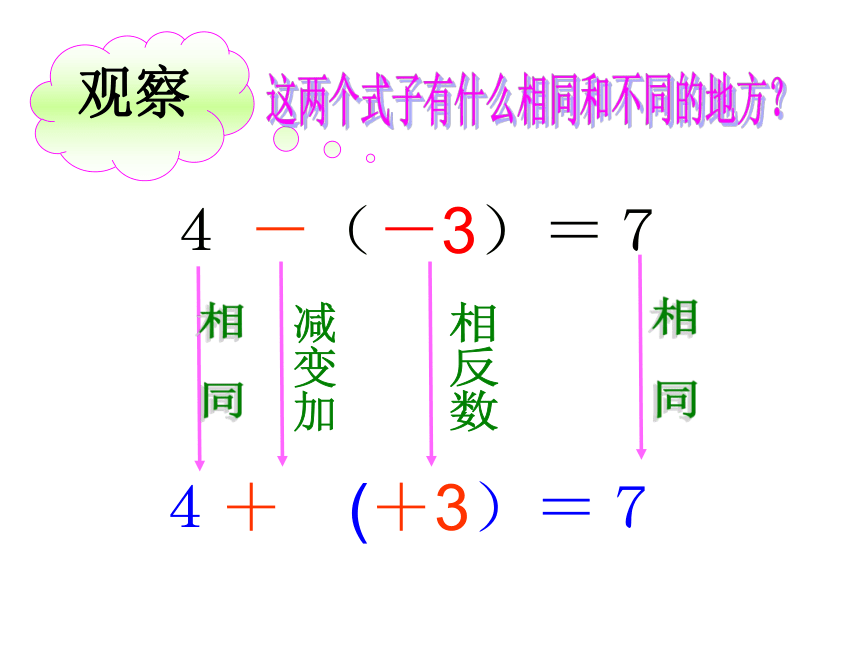
这两个式子有什么相同和不同的地方?
4 -(-3)=7
4+ (+3)=7
观察
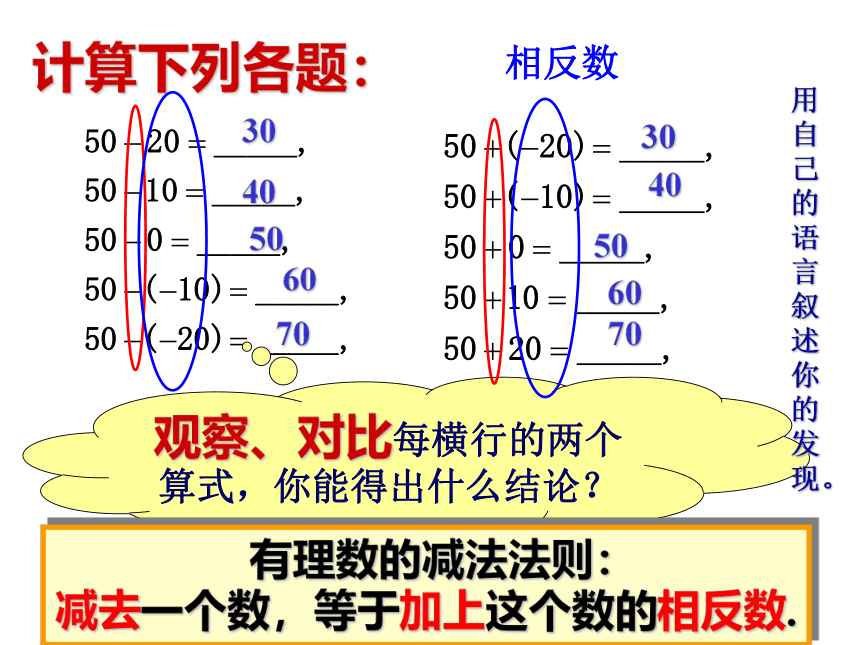
计算下列各题:
30
30
40
40
50
60
70
50
60
70
观察、对比每横行的两个算式,你能得出什么结论?
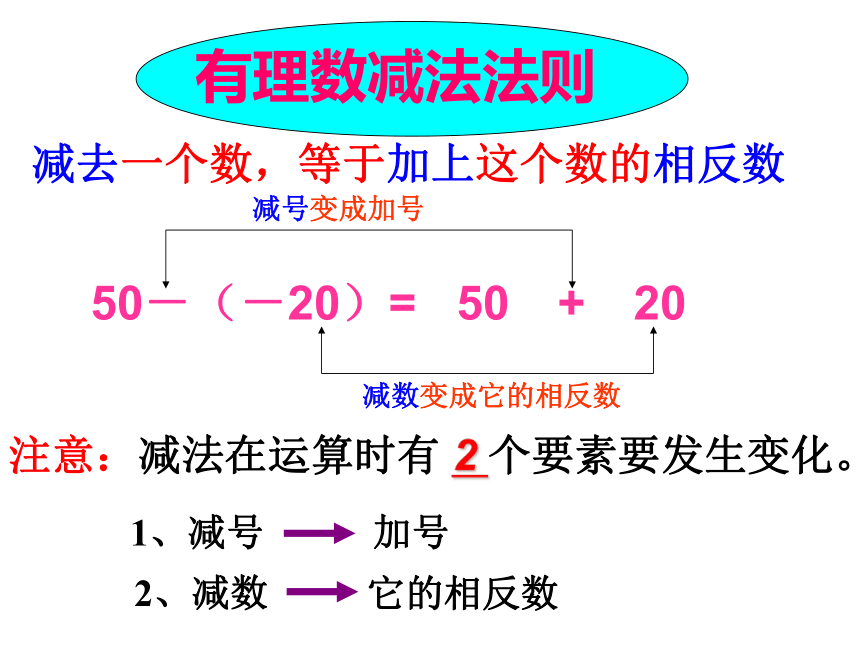
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
用自己的语言叙述你的发现。
相反数
减去一个数,等于加上这个数的相反数
有理数减法法则
注意:减法在运算时有 2 个要素要发生变化。
1、减号
加号
它的相反数
2、减数
50-(-20)= 50 + 20
减号变成加号
减数变成它的相反数
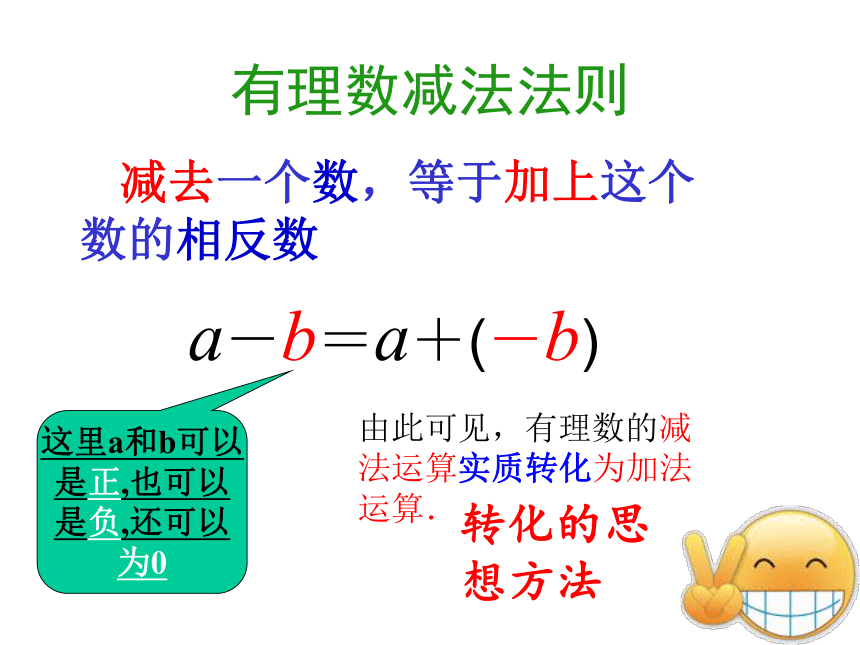
有理数减法法则
减去一个数,等于加上这个数的相反数
a-b=a+(-b)
这里a和b可以
是正,也可以
是负,还可以
为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
1.根据有理数减法的法则,将下面甲乙两组相同结果的算式连线。
(4)-3-(-4)
(1)3-(-4)
(2) 3-4
(3) (-3)-4
(D)-3+(-4)
(A) 3+ (-4)
(B) (-3)+4
(C) 3+4
甲
乙
练一练
2. 下列括号内各应填什么数?
(1) (+2)-(-3)=(+2)+( );
(2) 0 - (-4)= 0 + ( );
(3) (-6) - 3 =(-6)+( );
(4) 1- ( ) = 1 +( -39);
(5) 6 – 22 = 6 +( );
(6)(-2)-( )=(-2)+(+7);
+3
+4
-3
+39
-22
-7
(4)
=
解:(1)9-(-5)= 9 +(+ 5)
= 14
减去(-5)等于加 -5 的相反数,变成做加法.
(2)(-3)- 1 =(-3)+(-1)
= -4
减去1等于加 1 的相反数,变成做加法.
(3) 7.2 – (-4.8) = 7.2 +4.8
= 12
减-4.8等于加4.8
例1 计算下列各题:
(1) 9 -(-5) (2) (-3)- 1
(3) 7.2 – (-4.8) (4)
例1、计算下列各题:
(1)5-(-5) (2)0-7-5
有理数的减法法则
减去一个数,等于加上这个数的相反数.
解法指导:
先把减法变加法,
再依加法法则计算.
做题时要想着法则
解:5-(-5)
=5 + 5
=10
(2)0-7-5
=0+(-7)+(-5)
=-7+(-5)
=-12
=(-1.3)+2.1
=2.1-1.3
=0.8
例1、计算下列各题:
(3)(-1.3)-(-2.1) (4)
1、口算:
(1)3-5=___;(2)3-(-5)=___;
(3)(-3)-5=______;(4)(-3)-(-5)=____;
=3+(-5)
=-2
=3+5
=8
=(-3)+(-5)
=-8
=(-3)+5
=2
(5)-6-(-6)=______;(6)-7-0=___;
(7)0-(-7)=______;(8)(-6)- 6=_____;
(9) 9 -(-11)=___;
=-6+6
=0
=-7+0
=-7
=0+7
=7
=(-6)+(-6)
=-12
=9+11
=20
(1)(+3)-(-2) (2)(-1)-(+2)
(3)0-(-3) (4)1-5
(5)(-23)-(-12) (6)(-1.3)-2.6
=(+3)+2
=+5
=(-1)+(-2)
=-3
=0+3
=+3
=1+(-5)
=-4
=(-23)+12
=-11
=(-1.3)+(-2.6)
=-3.9
随堂练习
(7)已知一个数与3的和是-10,求这个数.
(-10)-(+3)
=(-10)+(-3)
=-13
计算
(1) 6 - 9
(2) (+4) - (-7)
(3) (-5) - (-8)
(4) 0 - (-5)
(5) (-2.5) - 5.9
(6) 1.9 – (-0.6)
课堂练习:
1.计算:(1) 3 - 5 ; (2) 3 -(- 5);
(3) (-3)-5; (4)(-3)-(-5);
(5) - 6 -(-6); (6) - 7 - 0;
(7) 0 -(-7); (8)(-6)- 6;
(9) 9 -(-11)-(-20);
(10)(-5)-(-5)-(+5);
3. 选择题:
(1)较小的数减去较大的数,所得的数一定是( )
A 0 B 正数 C 负数 D 0或负数
(2)下列说法正确的是( )
A 减去一个 负数,差一定大于被减数;
B 减去一个正数,差不一定小于被减数;
C 0 减去任何数,差都是负数;
D 两个数之差一定小于被减数;
A
C
畅谈所得 感悟提升
1、通过上面的练习,你能总结出有理数减法与小学里学过的减法的不同点吗?
(1)被减数可以小于减数.如: 1-5 ;
(2)差可以大于被减数,如:(+3)-(-2);
(3)有理数相减,差仍为有理数;
(4)大数减小数,差为正数;小数减大数,差为负数;
2、根据有理数减法的法则,一切加法和减法的运算,都可以统一成加法运算.
课堂小结
有理数的减法法则
减去一个数,等于加上这个数的相反数.
数学思想方法
转化的思想方法
a-b=a+(-b)
计算:
(1) (-72) -(-37) -(-22) -17
(2) (-16) -(-12) -24- (-18)
(3) 〔7+(-5) 〕- 12
(4) 3/2 -〔(-1.7)+ 0.7〕
机动
1.已知有理数a、b在数轴上的位置如图,试表示下列各式的符号:
⑴a+b__0; ⑵a-b___0;
⑶b-a___0; ⑷(b-a)-(a+b)___0
a
b
0
A.正数 B.负数 C.0 D.以上都有可能
B
3.两个有理数的差是-5,这两个有理数各是多少?请按下列要求,分别写出一个具体的算式:
(1)两个有理数都是正数;
(2)两个有理数都是负数;
(3)两个有理数异号.
在数轴上,点A、B、C、D表示的有理数分别是+1,+5,-2,-3,请问以下两点间的距离是多少:
(1)A、B两点;
(2)C、D两点;
(3)A、D两点;
两点所表示的有理数的差与两点间的距离有什么关系吗?
?
有理数的减法
1.3.2
1、理解并掌握有理数的减法法则,能进行有理数的减法运算。
2、能正确完成减法到加法的转化,培养自身的观察能力和思维能力
异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
一个数与0相加,仍得这个数.
(1) ( +4) + (+16) =
(2)(–2)+(–27)=
(3)(–9)+ 10 =
(4) 45 +(–60)=
(5)(–7)+ 7 =
(6) 16 + 0 =
(7) 0 + (–8) =
20
–29
1
–15
16
–8
同号两数相加,取与加数相同的符号,并把绝对值相加.
0
互为相反数的两个数相加得0.
温故而知新
0
1
2
3
-1
-2
-3
-4
4
这一天内杭州的温差是多少呢?
某一天杭州的最高温度是40C,最低温度是-30C
用到什么运算呢?
4 -(-3)= ?
0
1
2
3
-1
-2
-3
-4
4
0
1
2
3
-1
-2
-3
-4
4
0
1
2
3
-1
-2
-3
-4
4
4
3
4 +3= 7
4 - (-3) = ?
7
-
=
温差是多少呢?
4 - (-3) = 7
这两个式子有什么相同和不同的地方?
4 -(-3)=7
4+ (+3)=7
观察
计算下列各题:
30
30
40
40
50
60
70
50
60
70
观察、对比每横行的两个算式,你能得出什么结论?
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
用自己的语言叙述你的发现。
相反数
减去一个数,等于加上这个数的相反数
有理数减法法则
注意:减法在运算时有 2 个要素要发生变化。
1、减号
加号
它的相反数
2、减数
50-(-20)= 50 + 20
减号变成加号
减数变成它的相反数
有理数减法法则
减去一个数,等于加上这个数的相反数
a-b=a+(-b)
这里a和b可以
是正,也可以
是负,还可以
为0
由此可见,有理数的减法运算实质转化为加法运算.
转化的思想方法
1.根据有理数减法的法则,将下面甲乙两组相同结果的算式连线。
(4)-3-(-4)
(1)3-(-4)
(2) 3-4
(3) (-3)-4
(D)-3+(-4)
(A) 3+ (-4)
(B) (-3)+4
(C) 3+4
甲
乙
练一练
2. 下列括号内各应填什么数?
(1) (+2)-(-3)=(+2)+( );
(2) 0 - (-4)= 0 + ( );
(3) (-6) - 3 =(-6)+( );
(4) 1- ( ) = 1 +( -39);
(5) 6 – 22 = 6 +( );
(6)(-2)-( )=(-2)+(+7);
+3
+4
-3
+39
-22
-7
(4)
=
解:(1)9-(-5)= 9 +(+ 5)
= 14
减去(-5)等于加 -5 的相反数,变成做加法.
(2)(-3)- 1 =(-3)+(-1)
= -4
减去1等于加 1 的相反数,变成做加法.
(3) 7.2 – (-4.8) = 7.2 +4.8
= 12
减-4.8等于加4.8
例1 计算下列各题:
(1) 9 -(-5) (2) (-3)- 1
(3) 7.2 – (-4.8) (4)
例1、计算下列各题:
(1)5-(-5) (2)0-7-5
有理数的减法法则
减去一个数,等于加上这个数的相反数.
解法指导:
先把减法变加法,
再依加法法则计算.
做题时要想着法则
解:5-(-5)
=5 + 5
=10
(2)0-7-5
=0+(-7)+(-5)
=-7+(-5)
=-12
=(-1.3)+2.1
=2.1-1.3
=0.8
例1、计算下列各题:
(3)(-1.3)-(-2.1) (4)
1、口算:
(1)3-5=___;(2)3-(-5)=___;
(3)(-3)-5=______;(4)(-3)-(-5)=____;
=3+(-5)
=-2
=3+5
=8
=(-3)+(-5)
=-8
=(-3)+5
=2
(5)-6-(-6)=______;(6)-7-0=___;
(7)0-(-7)=______;(8)(-6)- 6=_____;
(9) 9 -(-11)=___;
=-6+6
=0
=-7+0
=-7
=0+7
=7
=(-6)+(-6)
=-12
=9+11
=20
(1)(+3)-(-2) (2)(-1)-(+2)
(3)0-(-3) (4)1-5
(5)(-23)-(-12) (6)(-1.3)-2.6
=(+3)+2
=+5
=(-1)+(-2)
=-3
=0+3
=+3
=1+(-5)
=-4
=(-23)+12
=-11
=(-1.3)+(-2.6)
=-3.9
随堂练习
(7)已知一个数与3的和是-10,求这个数.
(-10)-(+3)
=(-10)+(-3)
=-13
计算
(1) 6 - 9
(2) (+4) - (-7)
(3) (-5) - (-8)
(4) 0 - (-5)
(5) (-2.5) - 5.9
(6) 1.9 – (-0.6)
课堂练习:
1.计算:(1) 3 - 5 ; (2) 3 -(- 5);
(3) (-3)-5; (4)(-3)-(-5);
(5) - 6 -(-6); (6) - 7 - 0;
(7) 0 -(-7); (8)(-6)- 6;
(9) 9 -(-11)-(-20);
(10)(-5)-(-5)-(+5);
3. 选择题:
(1)较小的数减去较大的数,所得的数一定是( )
A 0 B 正数 C 负数 D 0或负数
(2)下列说法正确的是( )
A 减去一个 负数,差一定大于被减数;
B 减去一个正数,差不一定小于被减数;
C 0 减去任何数,差都是负数;
D 两个数之差一定小于被减数;
A
C
畅谈所得 感悟提升
1、通过上面的练习,你能总结出有理数减法与小学里学过的减法的不同点吗?
(1)被减数可以小于减数.如: 1-5 ;
(2)差可以大于被减数,如:(+3)-(-2);
(3)有理数相减,差仍为有理数;
(4)大数减小数,差为正数;小数减大数,差为负数;
2、根据有理数减法的法则,一切加法和减法的运算,都可以统一成加法运算.
课堂小结
有理数的减法法则
减去一个数,等于加上这个数的相反数.
数学思想方法
转化的思想方法
a-b=a+(-b)
计算:
(1) (-72) -(-37) -(-22) -17
(2) (-16) -(-12) -24- (-18)
(3) 〔7+(-5) 〕- 12
(4) 3/2 -〔(-1.7)+ 0.7〕
机动
1.已知有理数a、b在数轴上的位置如图,试表示下列各式的符号:
⑴a+b__0; ⑵a-b___0;
⑶b-a___0; ⑷(b-a)-(a+b)___0
a
b
0
A.正数 B.负数 C.0 D.以上都有可能
B
3.两个有理数的差是-5,这两个有理数各是多少?请按下列要求,分别写出一个具体的算式:
(1)两个有理数都是正数;
(2)两个有理数都是负数;
(3)两个有理数异号.
在数轴上,点A、B、C、D表示的有理数分别是+1,+5,-2,-3,请问以下两点间的距离是多少:
(1)A、B两点;
(2)C、D两点;
(3)A、D两点;
两点所表示的有理数的差与两点间的距离有什么关系吗?
?
