2019-2020学年黑龙江省绥化市肇东七中、十一中联考八年级下学期期末数学试卷(五四学制) ( word版,含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省绥化市肇东七中、十一中联考八年级下学期期末数学试卷(五四学制) ( word版,含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 697.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-28 06:28:37 | ||
图片预览



文档简介
2019-2020学年黑龙江省绥化市肇东七中、十一中联考八年级第二学期期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.关于x的一元二次方程x2﹣ax=5的一个根是﹣1,则a的值是( )
A.﹣1 B.1 C.4 D.﹣4
3.下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起
B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0
D.打开电视机,正在播放广告
4.已知⊙O的半径为3,圆心O到直线L的距离为4,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
5.二次函数y=(x+2)2﹣1的图象大致为( )
A. B.
C. D.
6.在平面直角坐标系中,将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
7.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B. C. D.
8.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
9.在图中,函数y=﹣ax2与y=ax+b的图象可能是( )
A. B.
C. D.
10.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.5π B.2.5π C.5+2.5π D.10
二.填空题(共10小题).
11.已知二次函数y=1﹣5x+3x2,则二次项系数a= ,一次项系数b= ,常数项c= .
12.关于x的方程xa﹣1+2x﹣5=0是一元二次方程,则a= .
13.如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
①AC=BC,②=,③=,④OC=CN
上述结论中,正确的有 (填序号)
14.二次函数y=2(x﹣3)2+4的最小值为 .
15.已知点A(a,1)与点B(5,b)是关于原点O的对称点,则a+b= .
16.已知点A(4,y1),B(﹣2,y2)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2的大小关系是 .(用“<”连接)
17.一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 cm2(用含π的式子表示)
18.不透明袋子中装有7个球,其中有3个红球,4个黄球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是红球的概率是 .
19.若抛物线y=ax2+bx+c的顶点是A(2,﹣1),且经过点B(1,0),则抛物线的函数关系式为 .
20.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .
三.解答题(共60分每小题10分)
21.用适当的方法解下列方程
(1)(x+3)2=5(x+3)
(2)2x2﹣x+3=0.
22.掷一个质地均匀的骰子,观察向下的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于6.
23.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB'C'.
(1)在正方形网格中,画出△AB'C';
(2)计算线段AB在旋转过程中所扫过的面积.
24.如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率.
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
26.如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
参考答案
一.选择题(共10小题).
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形与中心对称图形的概念判断即可.
解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、是轴对称图形,也是中心对称图形,故此选项符合题意;
C、是轴对称图形,不是中心对称图形,故此选项不合题意;
D、不是轴对称图形,是中心对称图形,故此选项不合题意.
故选:B.
2.关于x的一元二次方程x2﹣ax=5的一个根是﹣1,则a的值是( )
A.﹣1 B.1 C.4 D.﹣4
【分析】由方程的解的定义,将x=﹣1代入方程,得到关于a的方程,解方程即可求得a的值.
解:∵关于x的一元二次方程x2﹣ax=5的一个根是﹣1,
∴1+a=5,
解得a=4.
故选:C.
3.下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起
B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0
D.打开电视机,正在播放广告
【分析】直接利用随机事件以及必然事件、不可能事件的定义分析得出答案.
解:A、明天的早晨,太阳从东方升起,是必然事件,不合题意;
B、13人中至少有两人同生肖,是必然事件,不合题意;
C、抛出一枚骰子,点数为0,是不可能事件,不合题意;
D、打开电视机,正在播放广告,是随机事件,符合题意.
故选:D.
4.已知⊙O的半径为3,圆心O到直线L的距离为4,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
【分析】欲求直线1与圆O的位置关系,关键是比较圆心到直线的距离d与圆半径r的大小关系.若d<r,则直线与圆相交;若d=r,则直线与圆相切;若d>r,则直线与圆相离.
解:∵圆半径r=3,圆心到直线的距离d=4.
故r=3<d=4,
∴直线与圆的位置关系是相离.
故选:C.
5.二次函数y=(x+2)2﹣1的图象大致为( )
A. B.
C. D.
【分析】根据函数解析式判断出抛物线的对称轴、开口方向和顶点坐标即可.
解:a=1>0,抛物线开口向上,
由解析式可知对称轴为x=﹣2,顶点坐标为(﹣2,﹣1).
故选:D.
6.在平面直角坐标系中,将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
【分析】根据图象的平移规律,可得答案.
解:将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,得到的抛物线的解析式是将抛物线y=(x﹣2+3)2+1+2,即:y=(x+1)2+3.
故选:C.
7.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B. C. D.
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
解:设圆锥底面的半径为r,
扇形的弧长为:=π,
∵圆锥的底面周长等于它的侧面展开图的弧长,
∴根据题意得2πr=π,
解得:r=.
故选:A.
8.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
【分析】观察图形可知,黑白图形都是互相对称的,故其面积相等,则图中阴影部分的面积即是长方形面积的一半.
解:根据题意观察图形可知,
长方形的面积=10×4=40cm2,
再根据中心对称的性质得:
图中阴影部分的面积即是长方形面积的一半,
则图中阴影部分的面积=×40=20cm2.
故选:A.
9.在图中,函数y=﹣ax2与y=ax+b的图象可能是( )
A. B.
C. D.
【分析】根据每一个选项中函数的图象,分别判断两个函数式a的符号是否相符,作出判断.
解:根据图象判断两函数式中,a的符号是否相符;
A、由函数y=﹣ax2的图象知a<0,由函数y=ax+b的图象知a>0,不相符;
B、由函数y=﹣ax2的图象知a>0,由函数y=ax+b的图象知a<0,不相符;
C、由函数y=﹣ax2的图象知a>0,由函数y=ax+b的图象知a<0,不相符;
D、由函数y=﹣ax2的图象知a<0,由函数y=ax+b的图象知a<0,相符.
故选:D.
10.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.5π B.2.5π C.5+2.5π D.10
【分析】如图,圆心O运动路径的长度=OE+弧EO的长,根据弧长公式计算即可.
解:如图,圆心O运动路径的长度=OE+弧EO的长=?2π?5+?2π?5=5π.
故选:A.
二.填空题(共30分)
11.已知二次函数y=1﹣5x+3x2,则二次项系数a= 3 ,一次项系数b= ﹣5 ,常数项c= 1 .
【分析】根据二次函数的定义,可得答案.
解:二次函数y=1﹣5x+3x2,则二次项系数a=3,一次项系数b=﹣5,常数项c=1,
故答案为:3,﹣5,1.
12.关于x的方程xa﹣1+2x﹣5=0是一元二次方程,则a= 3 .
【分析】根据一元二次方程的定义可得a﹣1=2,再解即可.
解:∵关于x的方程xa﹣1+2x﹣5=0是一元二次方程,
∴a﹣1=2,
解得:a=3,
故答案为:3.
13.如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
①AC=BC,②=,③=,④OC=CN
上述结论中,正确的有 ①②③ (填序号)
【分析】根据垂径定理对各小题进行逐一分析即可.
解:∵在⊙O中,MN是直径,AB是弦,且MN⊥AB,
∴AC=BC,=,=,故①②③真确;
∵AB不一定过ON的中点,
∴OC与CN的关系不能确定.
故答案为:①②③.
14.二次函数y=2(x﹣3)2+4的最小值为 4 .
【分析】根据二次函数的顶点式直接写出即可.
解:二次函数y=2(x﹣3)2+4的最小值为4.
故答案为:4.
15.已知点A(a,1)与点B(5,b)是关于原点O的对称点,则a+b= ﹣6 .
【分析】根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可直接得到a、b的值,再算出a+b即可.
解:∵点A(a,1)与点B(5,b)是关于原点O的对称点,
∴a=﹣5,b=﹣1,
∴a+b=﹣6.
故答案为:﹣6.
16.已知点A(4,y1),B(﹣2,y2)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2的大小关系是 y1<y2 .(用“<”连接)
【分析】分别计算自变量为4和﹣2时的函数值,然后比较函数值的大小即可.
解:当x=4时,y1=(x﹣2)2﹣1=3;当x=﹣2时,y2=(x﹣2)2﹣1=15,
所以y1<y2.
故答案为y1<y2.
17.一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 3π cm2(用含π的式子表示)
【分析】利用扇形面积公式计算即可得到结果.
解:根据题意得:S=Rl=×2π×3=3π,
则此扇形的面积为3πcm2,
故答案为:3π
18.不透明袋子中装有7个球,其中有3个红球,4个黄球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是红球的概率是 .
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解:∵袋子中共有7个球,其中红球有3个,
∴从袋子中随机取出1个球,它是红球的概率是,
故答案为:.
19.若抛物线y=ax2+bx+c的顶点是A(2,﹣1),且经过点B(1,0),则抛物线的函数关系式为 y=x2﹣4x+3 .
【分析】设抛物线的解析式为y=a(x﹣2)2﹣1,将点B(1,0)代入解析式即可求出a的值,从而得到二次函数解析式.
解:设抛物线的解析式为y=a(x﹣2)2﹣1,
将B(1,0)代入y=a(x﹣2)2﹣1得,
a=1,
函数解析式为y=(x﹣2)2﹣1,
展开得y=x2﹣4x+3.
故答案为:y=x2﹣4x+3.
20.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= 20° .
【分析】根据切线的性质可知∠PAC=90°,由切线长定理得PA=PB,∠P=40°,求出∠PAB的度数,用∠PAC﹣∠PAB得到∠BAC的度数.
解:∵PA是⊙O的切线,AC是⊙O的直径,
∴∠PAC=90°.
∵PA,PB是⊙O的切线,
∴PA=PB,
∵∠P=40°,
∴∠PAB=(180°﹣∠P)÷2=(180°﹣40°)÷2=70°,
∴∠BAC=∠PAC﹣∠PAB=90°﹣70°=20°.
故答案是:20°.
三.解答题(共60分每小题10分)
21.用适当的方法解下列方程
(1)(x+3)2=5(x+3)
(2)2x2﹣x+3=0.
【分析】(1)方程整理后,利用因式分解法求出解即可;
(2)方程利用公式法求出解即可.
解:(1)方程移项得:(x+3)2﹣5(x+3)=0,
分解因式得:(x+3)(x+3﹣5)=0,
解得:x1=﹣3,x2=2;
(2)2x2﹣x+3=0,
∵a=2,b=﹣1,c=3,
∴b2﹣4ac=1﹣24=﹣23<0,
则此方程无解.
22.掷一个质地均匀的骰子,观察向下的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于6.
【分析】根据概率的求法,找准两点:
1、全部情况的总数;
2、符合条件的情况数目;二者的比值就是其发生的概率.
解:(1)P(点数为2)=;
(2)点数为奇数的有3种可能,即点数为1,3,5,则P(点数为奇数)==;
(3)点数大于2且小于6的有3种可能,即点数为3,4,5,
则P(点数大于2且小于6)==.
23.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB'C'.
(1)在正方形网格中,画出△AB'C';
(2)计算线段AB在旋转过程中所扫过的面积.
【分析】(1)分别作出点B、C绕点A按顺时针方向旋转90°得到的对应点,再顺次连接可得;
(2)根据扇形的面积公式列式计算可得.
解:(1)如图所示,△AB'C'即为所求;
(2)因为AB==5,
所以线段AB在旋转过程中所扫过的面积为=π.
24.如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
【分析】(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
【解答】(1)证明:如图,连接OC.
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)解:在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD==5,
∴BD=OD﹣OB=5﹣3=2.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率.
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
【分析】(1)根据增长率问题应用题的等量关系列出方程即可求解;
(2)根据(1)所求得月平均增长率即可求得六月份的快递件数.
解:(1)设该快递公司投递总件数的月平均增长率为x,
根据题意,得
10(1+x)2=12.1
解方程得,
x1=0.1,x2=﹣2.1(不符合题意,舍去)
答:该快递公司投递总件数的月平均增长率为10%.
(2)该公司六月份的快递件数为:12.1(1+10%)=13.31(万件).
答:该公司六月份的快递件数将达到13.31万件.
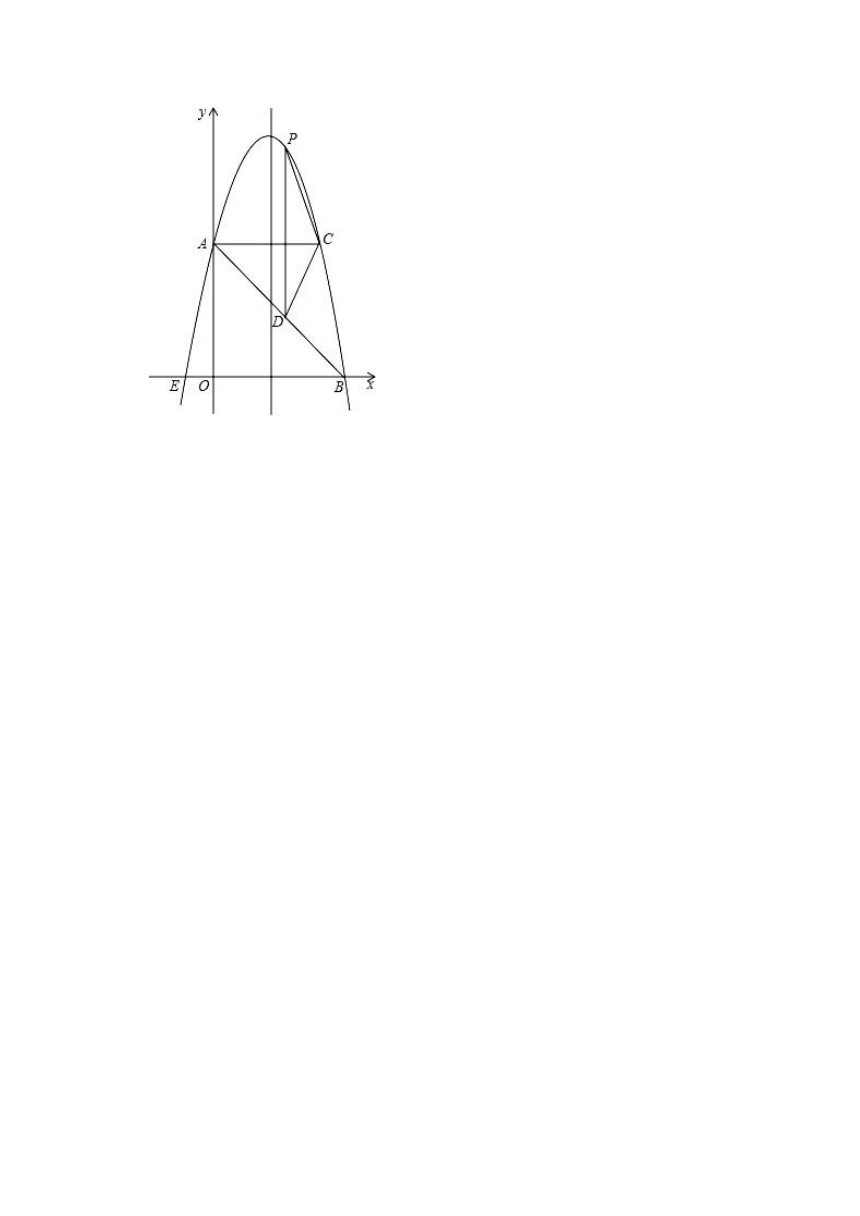
26.如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
【分析】(1)用待定系数法求抛物线解析式,并利用配方法求顶点坐标;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值;可得P的坐标.
解:(1)把点A(0,5),点B坐标为(5,0)代入抛物线y=ax2+4x+c中,
得:,解得:,
∴抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴顶点坐标为(2,9);
(2)设直线AB的解析式为:y=mx+n,
∵A(0,5),B(5,0),
∴,
解得:,
∴直线AB的解析式为:y=﹣x+5,
设P(x,﹣x2+4x+5),则D(x,﹣x+5),
∴PD=(﹣x2+4x+5)﹣(﹣x+5)=﹣x2+5x,
∵点C在抛物线上,且纵坐标为5,
∴C(4,5),
∴AC=4,
∴S四边形APCD=AC?PD=×4(﹣x2+5x)=﹣2x2+10x=﹣2(x﹣)2+,
∵﹣2<0,
∴S有最大值,
∴当x=时,S有最大值为,
此时P(,).
一、选择题(共10小题).
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.关于x的一元二次方程x2﹣ax=5的一个根是﹣1,则a的值是( )
A.﹣1 B.1 C.4 D.﹣4
3.下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起
B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0
D.打开电视机,正在播放广告
4.已知⊙O的半径为3,圆心O到直线L的距离为4,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
5.二次函数y=(x+2)2﹣1的图象大致为( )
A. B.
C. D.
6.在平面直角坐标系中,将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
7.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B. C. D.
8.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
9.在图中,函数y=﹣ax2与y=ax+b的图象可能是( )
A. B.
C. D.
10.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.5π B.2.5π C.5+2.5π D.10
二.填空题(共10小题).
11.已知二次函数y=1﹣5x+3x2,则二次项系数a= ,一次项系数b= ,常数项c= .
12.关于x的方程xa﹣1+2x﹣5=0是一元二次方程,则a= .
13.如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
①AC=BC,②=,③=,④OC=CN
上述结论中,正确的有 (填序号)
14.二次函数y=2(x﹣3)2+4的最小值为 .
15.已知点A(a,1)与点B(5,b)是关于原点O的对称点,则a+b= .
16.已知点A(4,y1),B(﹣2,y2)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2的大小关系是 .(用“<”连接)
17.一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 cm2(用含π的式子表示)
18.不透明袋子中装有7个球,其中有3个红球,4个黄球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是红球的概率是 .
19.若抛物线y=ax2+bx+c的顶点是A(2,﹣1),且经过点B(1,0),则抛物线的函数关系式为 .
20.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .
三.解答题(共60分每小题10分)
21.用适当的方法解下列方程
(1)(x+3)2=5(x+3)
(2)2x2﹣x+3=0.
22.掷一个质地均匀的骰子,观察向下的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于6.
23.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB'C'.
(1)在正方形网格中,画出△AB'C';
(2)计算线段AB在旋转过程中所扫过的面积.
24.如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率.
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
26.如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
参考答案
一.选择题(共10小题).
1.下列图形中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形与中心对称图形的概念判断即可.
解:A、是轴对称图形,不是中心对称图形,故此选项不合题意;
B、是轴对称图形,也是中心对称图形,故此选项符合题意;
C、是轴对称图形,不是中心对称图形,故此选项不合题意;
D、不是轴对称图形,是中心对称图形,故此选项不合题意.
故选:B.
2.关于x的一元二次方程x2﹣ax=5的一个根是﹣1,则a的值是( )
A.﹣1 B.1 C.4 D.﹣4
【分析】由方程的解的定义,将x=﹣1代入方程,得到关于a的方程,解方程即可求得a的值.
解:∵关于x的一元二次方程x2﹣ax=5的一个根是﹣1,
∴1+a=5,
解得a=4.
故选:C.
3.下列事件属于随机事件的是( )
A.明天的早晨,太阳从东方升起
B.13人中至少有两人同生肖
C.抛出一枚骰子,点数为0
D.打开电视机,正在播放广告
【分析】直接利用随机事件以及必然事件、不可能事件的定义分析得出答案.
解:A、明天的早晨,太阳从东方升起,是必然事件,不合题意;
B、13人中至少有两人同生肖,是必然事件,不合题意;
C、抛出一枚骰子,点数为0,是不可能事件,不合题意;
D、打开电视机,正在播放广告,是随机事件,符合题意.
故选:D.
4.已知⊙O的半径为3,圆心O到直线L的距离为4,则直线L与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
【分析】欲求直线1与圆O的位置关系,关键是比较圆心到直线的距离d与圆半径r的大小关系.若d<r,则直线与圆相交;若d=r,则直线与圆相切;若d>r,则直线与圆相离.
解:∵圆半径r=3,圆心到直线的距离d=4.
故r=3<d=4,
∴直线与圆的位置关系是相离.
故选:C.
5.二次函数y=(x+2)2﹣1的图象大致为( )
A. B.
C. D.
【分析】根据函数解析式判断出抛物线的对称轴、开口方向和顶点坐标即可.
解:a=1>0,抛物线开口向上,
由解析式可知对称轴为x=﹣2,顶点坐标为(﹣2,﹣1).
故选:D.
6.在平面直角坐标系中,将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,所得抛物线的解析式为( )
A.y=(x+1)2﹣1 B.y=(x﹣5)2﹣1 C.y=(x+1)2+3 D.y=(x﹣5)2+3
【分析】根据图象的平移规律,可得答案.
解:将抛物线y=(x﹣2)2+1先向上平移2个单位长度,再向左平移3个单位长度,得到的抛物线的解析式是将抛物线y=(x﹣2+3)2+1+2,即:y=(x+1)2+3.
故选:C.
7.用一个圆心角为120°,半径为4的扇形作一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B. C. D.
【分析】根据扇形的弧长公式求出弧长,根据圆锥的底面周长等于它的侧面展开图的弧长求出半径.
解:设圆锥底面的半径为r,
扇形的弧长为:=π,
∵圆锥的底面周长等于它的侧面展开图的弧长,
∴根据题意得2πr=π,
解得:r=.
故选:A.
8.如图,已知长方形的长为10cm,宽为4cm,则图中阴影部分的面积为( )
A.20cm2 B.15cm2 C.10cm2 D.25cm2
【分析】观察图形可知,黑白图形都是互相对称的,故其面积相等,则图中阴影部分的面积即是长方形面积的一半.
解:根据题意观察图形可知,
长方形的面积=10×4=40cm2,
再根据中心对称的性质得:
图中阴影部分的面积即是长方形面积的一半,
则图中阴影部分的面积=×40=20cm2.
故选:A.
9.在图中,函数y=﹣ax2与y=ax+b的图象可能是( )
A. B.
C. D.
【分析】根据每一个选项中函数的图象,分别判断两个函数式a的符号是否相符,作出判断.
解:根据图象判断两函数式中,a的符号是否相符;
A、由函数y=﹣ax2的图象知a<0,由函数y=ax+b的图象知a>0,不相符;
B、由函数y=﹣ax2的图象知a>0,由函数y=ax+b的图象知a<0,不相符;
C、由函数y=﹣ax2的图象知a>0,由函数y=ax+b的图象知a<0,不相符;
D、由函数y=﹣ax2的图象知a<0,由函数y=ax+b的图象知a<0,相符.
故选:D.
10.如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
A.5π B.2.5π C.5+2.5π D.10
【分析】如图,圆心O运动路径的长度=OE+弧EO的长,根据弧长公式计算即可.
解:如图,圆心O运动路径的长度=OE+弧EO的长=?2π?5+?2π?5=5π.
故选:A.
二.填空题(共30分)
11.已知二次函数y=1﹣5x+3x2,则二次项系数a= 3 ,一次项系数b= ﹣5 ,常数项c= 1 .
【分析】根据二次函数的定义,可得答案.
解:二次函数y=1﹣5x+3x2,则二次项系数a=3,一次项系数b=﹣5,常数项c=1,
故答案为:3,﹣5,1.
12.关于x的方程xa﹣1+2x﹣5=0是一元二次方程,则a= 3 .
【分析】根据一元二次方程的定义可得a﹣1=2,再解即可.
解:∵关于x的方程xa﹣1+2x﹣5=0是一元二次方程,
∴a﹣1=2,
解得:a=3,
故答案为:3.
13.如图,在⊙O中,MN是直径,AB是弦,且MN⊥AB,垂足为C,下列结论:
①AC=BC,②=,③=,④OC=CN
上述结论中,正确的有 ①②③ (填序号)
【分析】根据垂径定理对各小题进行逐一分析即可.
解:∵在⊙O中,MN是直径,AB是弦,且MN⊥AB,
∴AC=BC,=,=,故①②③真确;
∵AB不一定过ON的中点,
∴OC与CN的关系不能确定.
故答案为:①②③.
14.二次函数y=2(x﹣3)2+4的最小值为 4 .
【分析】根据二次函数的顶点式直接写出即可.
解:二次函数y=2(x﹣3)2+4的最小值为4.
故答案为:4.
15.已知点A(a,1)与点B(5,b)是关于原点O的对称点,则a+b= ﹣6 .
【分析】根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可直接得到a、b的值,再算出a+b即可.
解:∵点A(a,1)与点B(5,b)是关于原点O的对称点,
∴a=﹣5,b=﹣1,
∴a+b=﹣6.
故答案为:﹣6.
16.已知点A(4,y1),B(﹣2,y2)都在二次函数y=(x﹣2)2﹣1的图象上,则y1、y2的大小关系是 y1<y2 .(用“<”连接)
【分析】分别计算自变量为4和﹣2时的函数值,然后比较函数值的大小即可.
解:当x=4时,y1=(x﹣2)2﹣1=3;当x=﹣2时,y2=(x﹣2)2﹣1=15,
所以y1<y2.
故答案为y1<y2.
17.一个扇形的半径为3cm,弧长为2πcm,则此扇形的面积为 3π cm2(用含π的式子表示)
【分析】利用扇形面积公式计算即可得到结果.
解:根据题意得:S=Rl=×2π×3=3π,
则此扇形的面积为3πcm2,
故答案为:3π
18.不透明袋子中装有7个球,其中有3个红球,4个黄球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是红球的概率是 .
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解:∵袋子中共有7个球,其中红球有3个,
∴从袋子中随机取出1个球,它是红球的概率是,
故答案为:.
19.若抛物线y=ax2+bx+c的顶点是A(2,﹣1),且经过点B(1,0),则抛物线的函数关系式为 y=x2﹣4x+3 .
【分析】设抛物线的解析式为y=a(x﹣2)2﹣1,将点B(1,0)代入解析式即可求出a的值,从而得到二次函数解析式.
解:设抛物线的解析式为y=a(x﹣2)2﹣1,
将B(1,0)代入y=a(x﹣2)2﹣1得,
a=1,
函数解析式为y=(x﹣2)2﹣1,
展开得y=x2﹣4x+3.
故答案为:y=x2﹣4x+3.
20.如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= 20° .
【分析】根据切线的性质可知∠PAC=90°,由切线长定理得PA=PB,∠P=40°,求出∠PAB的度数,用∠PAC﹣∠PAB得到∠BAC的度数.
解:∵PA是⊙O的切线,AC是⊙O的直径,
∴∠PAC=90°.
∵PA,PB是⊙O的切线,
∴PA=PB,
∵∠P=40°,
∴∠PAB=(180°﹣∠P)÷2=(180°﹣40°)÷2=70°,
∴∠BAC=∠PAC﹣∠PAB=90°﹣70°=20°.
故答案是:20°.
三.解答题(共60分每小题10分)
21.用适当的方法解下列方程
(1)(x+3)2=5(x+3)
(2)2x2﹣x+3=0.
【分析】(1)方程整理后,利用因式分解法求出解即可;
(2)方程利用公式法求出解即可.
解:(1)方程移项得:(x+3)2﹣5(x+3)=0,
分解因式得:(x+3)(x+3﹣5)=0,
解得:x1=﹣3,x2=2;
(2)2x2﹣x+3=0,
∵a=2,b=﹣1,c=3,
∴b2﹣4ac=1﹣24=﹣23<0,
则此方程无解.
22.掷一个质地均匀的骰子,观察向下的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于6.
【分析】根据概率的求法,找准两点:
1、全部情况的总数;
2、符合条件的情况数目;二者的比值就是其发生的概率.
解:(1)P(点数为2)=;
(2)点数为奇数的有3种可能,即点数为1,3,5,则P(点数为奇数)==;
(3)点数大于2且小于6的有3种可能,即点数为3,4,5,
则P(点数大于2且小于6)==.
23.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB'C'.
(1)在正方形网格中,画出△AB'C';
(2)计算线段AB在旋转过程中所扫过的面积.
【分析】(1)分别作出点B、C绕点A按顺时针方向旋转90°得到的对应点,再顺次连接可得;
(2)根据扇形的面积公式列式计算可得.
解:(1)如图所示,△AB'C'即为所求;
(2)因为AB==5,
所以线段AB在旋转过程中所扫过的面积为=π.
24.如图,AB是⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠BCD=∠A.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为3,CD=4,求BD的长.
【分析】(1)连接OC,由AB是⊙O的直径可得出∠ACB=90°,即∠ACO+∠OCB=90°,由等腰三角形的性质结合∠BCD=∠A,即可得出∠OCD=90°,即CD是⊙O的切线;
(2)在Rt△OCD中,由勾股定理可求出OD的值,进而可得出BD的长.
【解答】(1)证明:如图,连接OC.
∵AB是⊙O的直径,C是⊙O上一点,
∴∠ACB=90°,即∠ACO+∠OCB=90°.
∵OA=OC,∠BCD=∠A,
∴∠ACO=∠A=∠BCD,
∴∠BCD+∠OCB=90°,即∠OCD=90°,
∴CD是⊙O的切线.
(2)解:在Rt△OCD中,∠OCD=90°,OC=3,CD=4,
∴OD==5,
∴BD=OD﹣OB=5﹣3=2.
25.现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率.
(2)如果按此速度增涨,该公司六月份的快递件数将达到多少万件?
【分析】(1)根据增长率问题应用题的等量关系列出方程即可求解;
(2)根据(1)所求得月平均增长率即可求得六月份的快递件数.
解:(1)设该快递公司投递总件数的月平均增长率为x,
根据题意,得
10(1+x)2=12.1
解方程得,
x1=0.1,x2=﹣2.1(不符合题意,舍去)
答:该快递公司投递总件数的月平均增长率为10%.
(2)该公司六月份的快递件数为:12.1(1+10%)=13.31(万件).
答:该公司六月份的快递件数将达到13.31万件.
26.如图,在平面直角坐标系中,抛物线y=ax2+4x+c与y轴交于点A(0,5),与x轴交于点E,B,点B坐标为(5,0).
(1)求二次函数解析式及顶点坐标;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
【分析】(1)用待定系数法求抛物线解析式,并利用配方法求顶点坐标;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立函数关系式S四边形APCD=﹣2x2+10x,根据二次函数求出极值;可得P的坐标.
解:(1)把点A(0,5),点B坐标为(5,0)代入抛物线y=ax2+4x+c中,
得:,解得:,
∴抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴顶点坐标为(2,9);
(2)设直线AB的解析式为:y=mx+n,
∵A(0,5),B(5,0),
∴,
解得:,
∴直线AB的解析式为:y=﹣x+5,
设P(x,﹣x2+4x+5),则D(x,﹣x+5),
∴PD=(﹣x2+4x+5)﹣(﹣x+5)=﹣x2+5x,
∵点C在抛物线上,且纵坐标为5,
∴C(4,5),
∴AC=4,
∴S四边形APCD=AC?PD=×4(﹣x2+5x)=﹣2x2+10x=﹣2(x﹣)2+,
∵﹣2<0,
∴S有最大值,
∴当x=时,S有最大值为,
此时P(,).
同课章节目录
