人教版(五四学制)数学七年级上册第十二章-相交线和平行线-单元测试(Word版 含解析)
文档属性
| 名称 | 人教版(五四学制)数学七年级上册第十二章-相交线和平行线-单元测试(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 138.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-28 00:00:00 | ||
图片预览




文档简介
第十二章-相交线与平行线
一、单选题
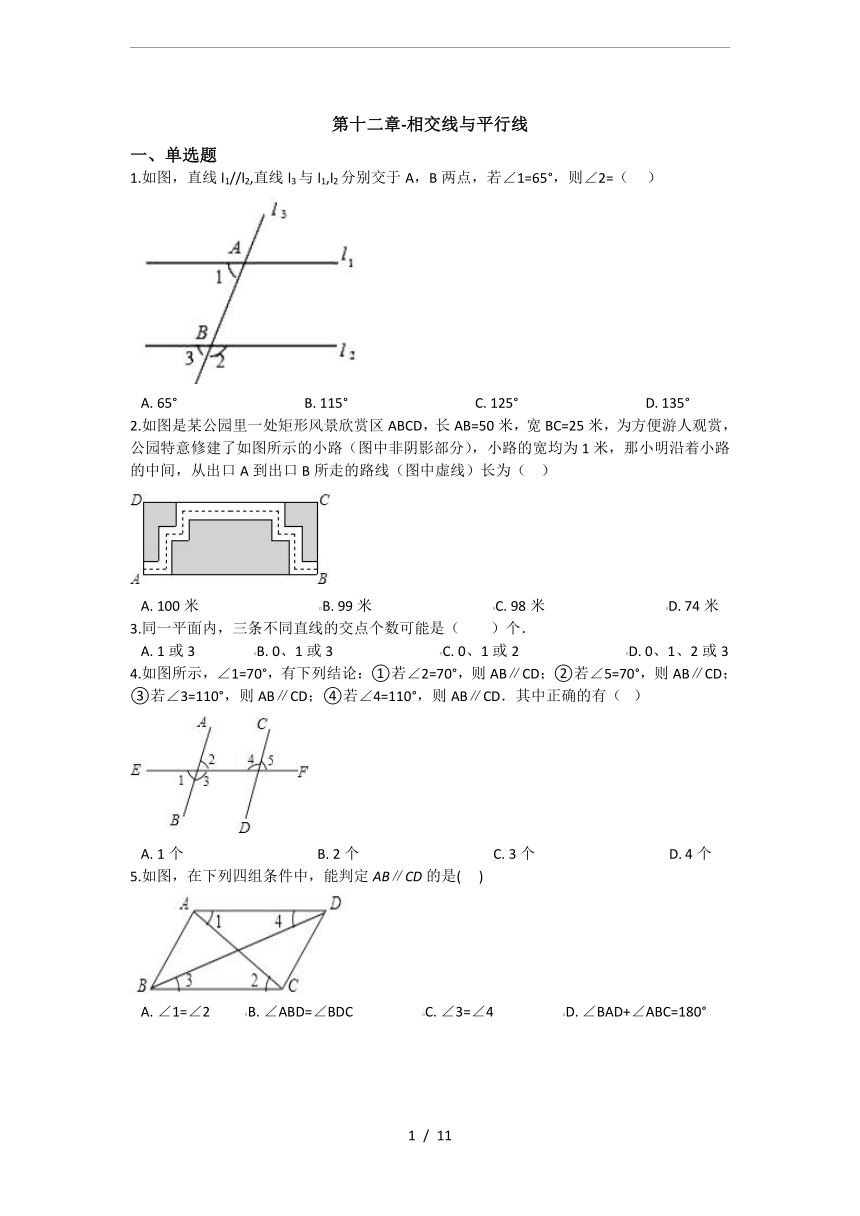
1.如图,直线l1//l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=(???
)
A.?65°?????????????????????????????????????B.?115°?????????????????????????????????????C.?125°?????????????????????????????????????D.?135°
2.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为(??
)
A.?100米???????????????????????????????????B.?99米???????????????????????????????????C.?98米???????????????????????????????????D.?74米
3.同一平面内,三条不同直线的交点个数可能是( )个.
A.?1或3?????????????????B.?0、1或3???????????????????????????????C.?0、1或2???????????????????????????????D.?0、1、2或3
4.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.如图,在下列四组条件中,能判定AB∥CD的是(???
)
A.?∠1=∠2??????????B.?∠ABD=∠BDC????????????????????C.?∠3=∠4????????????????????D.?∠BAD+∠ABC=180°
6.如图所示,下列说法正确的是(??
)
A.?∠1和∠2是内错角??????????
B.?∠1和∠5是同位角??????????
C.?∠1和∠2是同旁内角??????????
D.?∠1和∠4是内错角
7.已知直线a、b、c相互平行,直线a与b的距离是4cm,直线b与c的距离是6cm,那么直线a与c的距离是(??
)
A.?2cm?????????????????????????????B.?5cm?????????????????????????????C.?2cm或5cm?????????????????????????????D.?2cm或10cm
8.如图,下列判断不正确的是(??
)
A.?因为∠1=∠4,所以DE∥AB????????????????????????????????????B.?因为∠2=∠3,所以AD∥EC
C.?因为∠5=∠A,所以AB∥DE????????????????????????????????????D.?因为∠ADE+∠BED=180°,所以AD∥BE
9.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.?A点??????????????????????????????????????B.?B点??????????????????????????????????????C.?C点??????????????????????????????????????D.?D点
10.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是(?
???)
A.?(-2,6)?????????????????????????B.?(-2,0)?????????????????????????C.?(-5,3)?????????????????????????D.?(1,3)
二、填空题
11.已知∠A的两边分别平行于∠B的两边,∠B=50°,则∠A的度数为________.
12.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=120°,则∠2=________°.
13.如图,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,则∠1+∠2=________.
14.一建筑物楼梯样式如图所示,经测量得出AB=3dm,BC=4dm,∠B=90°,CD=1dm,DE=1.5dm,EF=DE,AC=2AG.根据这些数据,试着计算出折线AC(即楼梯表面AJIHGFEDC)的长度为________.
15.如图,直线AB、CD被EF、EC所截,在∠1、∠2、∠3、∠4、∠5、∠6中,同位角有________个.
16.如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
17.如图,MN分别交AB、CD于点E、F,AB∥CD,∠AEM=80°,则∠DFN为________.
18.把图形进行平移,在下列特征中:
①图形的形状;②图形的位置;③线段的长度;④角的大小;⑤垂直关系;⑥平行关系.
不发生改变的有________(把你认为正确的序号都填上).
三、解答题
19.如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=63°,∠2=63°,且∠C=∠D.求证:∠A=∠F.
20.如图,EF∥AD,∠1=∠2,将求证AB∥DG的过程填空完整.
证明:∵EF∥AD(????????????????????
)
∴∠2=
????????????????????
(
????????????????????
)
又∵∠1=∠2(
????????????????????
)
∴∠1=∠3(
????????????????????
)
∴AB∥
????????????????????
(
????????????????????
)
四、综合题
21.如图,在平面网格中每个小正方形的边长为1.
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
22.如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
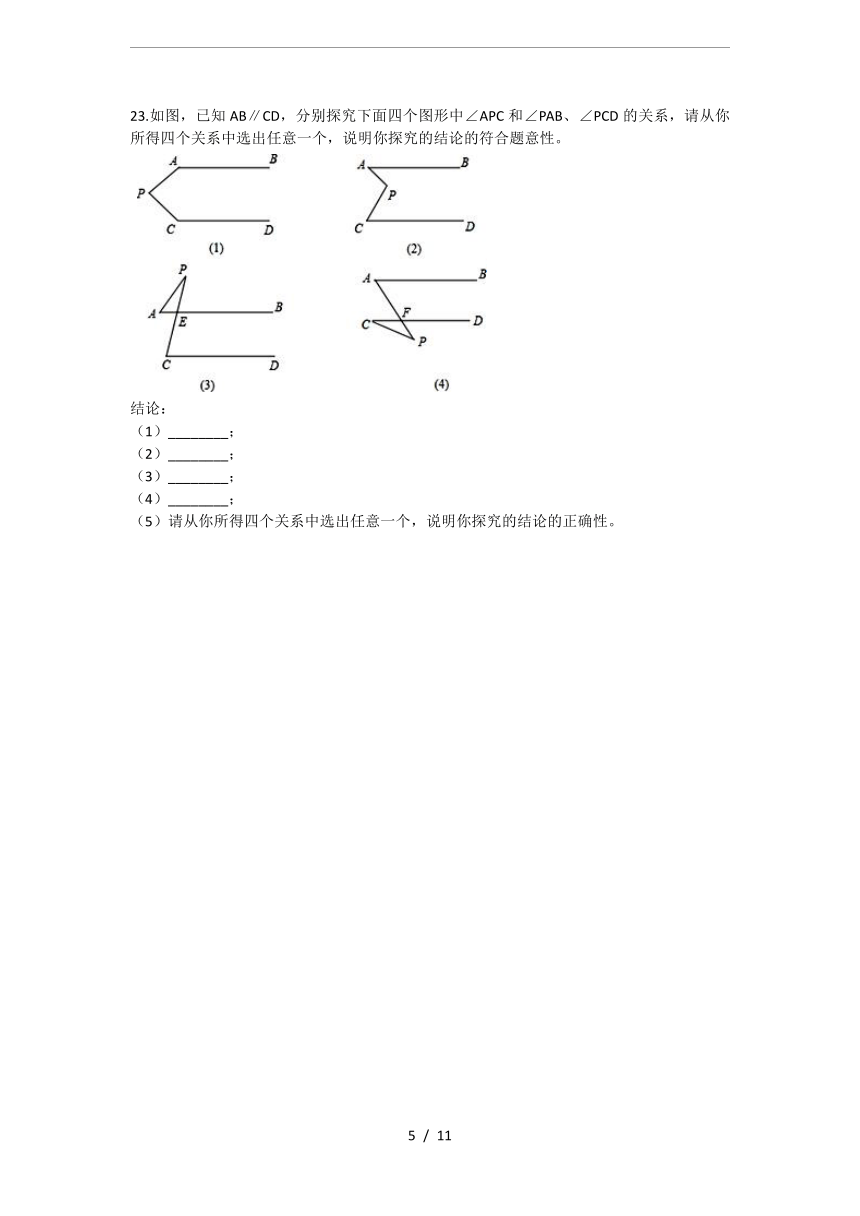
23.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的符合题意性。
结论:
(1)________;
(2)________;
(3)________;
(4)________;
(5)请从你所得四个关系中选出任意一个,说明你探究的结论的正确性。
答案
一、单选题
1.【答案】
B
【解析】【解答】解:因为直线l1//l2,
所以∠3=∠1=65°,
又因为∠3+∠2=180°,
所以∠2=180°-65=115°
故选B。
【分析】由平行线的性质可得同位角相等,即∠3=∠1,又由平角的定义可得∠3+∠2=180°,即可求出。
2.【答案】C
【解析】【解答】解:利用已知可以得出此图形可以分为横向与纵向分析,横距离等于AB,纵向距离等于(AD﹣1)×2,图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为50+(25﹣1)×2=98米,故答案为:C.
【分析】观察图形可得到横距离等于AB,纵向距离等于(AD﹣1)×2,即可求解。
3.【答案】
D
【解析】【解答】解:如图,三条直线的交点个数可能是0或1或2或3.
故选D.
【分析】根据两直线平行和相交的定义作出图形即可得解.
4.【答案】
B
【解析】【解答】解:①由∠1=∠2=70°,无法得出AB∥CD,故此选项错误;
②∵∠1=70°,
∴∠2=70°,
∵∠5=∠2=70°,
∴AB∥CD,故此选项正确;
③由∠3=110°,无法得出AB∥CD,故此选项错误;
④∵∠1=70°,
∴∠2=70°,
∵∠4=110°,
∴∠5=70°,
∴∠5=∠2=70°,
∴AB∥CD,故此选项正确;
∴其中正确的有2个.
故选:B.
【分析】直接利用邻补角的定义,结合对顶角的性质以及平行线的判定方法分析得出答案.
5.【答案】
B
【解析】【解答】A.因为∠1=∠2,而且∠1与∠2是内错角,则AD//BC,不符合;
B.因为∠ABD=∠BDC,而且∠ABD与∠BDC是内错角,则AB//CD,符合;
C.因为∠3=∠4,而且∠3与∠4是内错角,则AD//BC,不符合;
D.因为∠BAD+∠ABC=180°,而且∠BAD与∠ABC是同旁内角,则AD//BC,不符合;
【分析】根据平行线的判定理去判断:(1)同位角相等,两直线平行;(2)内错角相等,
两直线平行;(3)同旁内角互补,两直线平行.
6.【答案】C
【解析】【解答】解:A、∠1和∠2是同旁内角,故错误;
B、∠1和∠5是不是同位角,故错误;
C、∠1和∠2是同旁内角,正确;
D、∠1和∠4不是同旁内角,故错误,
故答案为:C.
【分析】利用“三线八角”的定义分别判断后即可确定正确的选项.
7.【答案】
D
【解析】【解答】当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为6cm,
∴a与c的距离=6cm﹣4cm=2cm;
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为6cm,
∴a与c的距离=6cm+4cm=10cm,
综上所述,a与c的距离为2cm或10cm.
故答案为:D.
【分析】分为直线c在a、b之间或直线c不在a、b之间两种情况,然后利用平行线间的距离的意义进行求解即可.
8.【答案】C
【解析】
【分析】根据题意,结合图形,对选项一一分析,选择正确答案.
【解答】A、因为∠1=∠4,所以DE∥AB,内错角相等,两直线平行,故选项正确;
B、因为∠2=∠3,所以AD∥BE,内错角相等,两直线平行,故选项正确;
C、因为∠5与∠A,不是同位角,所以不能判定AB∥DE,故选项错误;
D、因为∠ADE+∠BED=180°,所以AD∥BE,同旁内角互补,两直线平行,故选项正确.
故选C.
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行
9.【答案】
A
【解析】【解答】解:根据垂线段最短可得:应建在A处,
故选:A.
【分析】根据垂线段最短可得答案.
10.【答案】D
【解析】【解答】将点P(-2,3)向右平移3个单位到Q点,即Q点的横坐标加3,纵坐标不变,
即Q点的坐标为(1,3),故答案为:D
【分析】根据P(-2,3)沿x轴方向向右平移3个单位则纵坐标不变,横坐标加3进行求解。
二、填空题
11.【答案】50°或130°
【解析】【解答】如图:∠B=50°或130°;故填50°或130°.
【分析】根据题意得到两种图形,由∠A的两边分别平行于∠B的两边,得到一种是∠A由∠B平移得到,故∠A=∠B;另一种是∠A与∠B是同旁内角;根据两直线平行,同旁内角互补,得到∠A的度数.
12.【答案】
60
【解析】【解答】解:过C作MC∥AB,∴∠B+∠BCM=180°.
∵∠ABC+∠BCD+∠CDE=360°,∴∠MCD+∠D=180°,∴MC∥ED,∴AB∥ED,∴∠AFG+∠2=180°.
∵∠1=120°,∴∠AFG=120°,∴∠2=180°-120°=60°.
故答案为:60.
【分析】过C作MC∥AB,根据二直线平行,同旁内角互补得出∠B+∠BCM=180°,从而根据等式的性质得出∠MCD+∠D=180°,根据同旁内角互补,两直线平行得出MC∥ED,根据平行于同一直线的两条直线互相平行得出AB∥ED,根据二直线平行,同旁内角互补得出∠AFG+∠2=180°,根据对顶角相等得出∠AFG=120°,从而即可算出答案。
13.【答案】
90°
【解析】【解答】解:∵CE、AE分别平分∠ACD、∠CAB,
∴∠1=∠DCE=∠ACD,∠2=∠BAE=∠CAB,
∴∠ACD=2∠1,∠CAB=2∠2,
又∵AB∥CD,
∴∠CAB+∠ACD=180°,
∴2∠2+2∠1=180°,
∴∠2+∠1=90°.
故答案为:90°.
【分析】根据角平分线定义得∠ACD=2∠1,∠CAB=2∠2,再由平行线性质得∠CAB+∠ACD=180°,代入、计算即可得出答案.
14.【答案】7dm
【解析】【解答】解:
由图可知:JI=AM,HG=MN,FE=NZ,CD=ZB,
AJ=BX,HI=XY,GF=YP,ED=PC,
∴计算出折线AC=(AJ+IH+GF+ED)+(JI+HG+EF+DC)=AB+BC=3+4=7(dm).
【分析】利用平移的性质,可得出折线AC的长就是AB+BC的值。
15.【答案】3
【解析】【解答】解:∠1与∠5是同位角,∠4与∠6是同位角,∠2与∠4是同位角,故答案为:3.
【分析】根据同位角的特点:两个角都在第三条直线的同旁,又分别处在被截的两条直线同侧的位置的角,呈“F”型,即可得出答案。
16.【答案】900
【解析】【解答】分别过E点,F点,G点,H点作
?平行于AB,
同旁内角,把这六个角转化一下,可得有5个180°的角,
∴180×5=900°.
【分析】分别过E点,F点,G点,H点作
l
1
,
l
2
,
l
3
,
l
4
?平行于AB,根据平行线的判定定理得出
l
1?∥
l
2?∥
l
3?∥
l
4?
∥AB∥CD
,再根据二直线平行同旁内角互补把这六个角转化一下,可得有5个180°的角,从而得出答案。
17.【答案】
80°
【解析】【解答】解:∵∠AEM=80°,
∴∠AEM=∠BEN=80°
∵AB∥CD
∴∠BEN=∠DFN=80°
故答案为:80°
【分析】根据对顶角相等求出∠BEN的度数,再根据平行线的性质证得∠BEN=∠DFN,就可得出答案。
18.【答案】①③④⑤⑥
【解析】【解答】解:由图形平移的性质,知图形在平移时,其特征不发生改变的有①③④⑤⑥.
故答案为:①③④⑤⑥.
【分析】根据平移的性质直接判断即可.
三、解答题
19.【答案】
证明:∵∠1=∠DMF,∠1=∠2=63°,
∴∠DMF=∠2,
∴DB∥CE,
∴∠C=∠DBA,
∵
∠C=∠D
,
∴∠DBA=∠D,
∴DF∥AC,
∴
∠A=∠F.
【解析】【分析】根据同位角相等两直线平行,可得DB∥CE,由两直线平行同位角相等可得∠C=∠DBA,利用内错角相等两直线平行可得
DF∥AC,最后根据两直线平行内错角相等,可得
∠A=∠F.
20.【答案】
已知;∠3;两直线平行,同位角相等;已知;等量代换;DG;内错角相等,两直线平行
【解析】【解答】证明:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平行)
【分析】此题根据平行线的性质、判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之,同位角相等,内错角相等,同旁内角互补,则两直线平行.
四、综合题
21.【答案】(1)解:将线段AB向右平移3个小格(向下平移4
个小格),再向下平移4个小格(向右平移3个小格),
得线段CD
(2)解:将线段BD向左平移3个小格(向下平移1个小格),再向下平移1个小格(向左平移3个小格),得到线段AC
【解析】【分析】在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
22.【答案】(1)解:∵AD∥BC,∠B=60
∴∠1=∠B=60°
∵∠1=∠C,
∴∠C=∠B=60°
(2)解:DE∥AB,理由如下:
∵AD∥BC,
∴∠C+∠ADC?=180°
∴∠ADC=180°-∠C=120°
∵DE是∠ADC的平分线,
∴∠ADE=
∠BDC=60°
∵∠1=∠B=60°
∴∠1=∠ADE.
∴DE∥AB.
【解析】【分析】(1)由AD//BC
,可知∠1=∠B=,又因为∠1=∠C,所以可知∠C=;
(2)同样由AD//BC
,同旁内角互补,可知∠ADC=,又因为DE平分∠ADC,结合三角形内角和定理可知,∠EDC=∠DEC=,所以∠B=∠DEC,AB//DE
.
23.【答案】
(1)∠APC+∠PAB+∠PCD=180°
(2)∠APC=∠PAB+∠PCD
(3)∠APC=∠PCD-∠PAB
(4)∠APC=∠PAB-∠PCD
(5)解:选择(1)
如图,过点P作PE∥CD则∠CPE+∠PCD=180°
∵CD∥AB
∴PE∥AB
∴∠APE+∠PAB=180°
∴∠APC+∠PAB+∠PCD=180°
【解析】【分析】根据两平行线间夹折线的解决方法:过折点做一条直线的平行线,证明它与另一条直线也平行,即可得到三条互相平行的直线,利用平行线的性质转化角的关系即可。
/
一、单选题
1.如图,直线l1//l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=(???
)
A.?65°?????????????????????????????????????B.?115°?????????????????????????????????????C.?125°?????????????????????????????????????D.?135°
2.如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为(??
)
A.?100米???????????????????????????????????B.?99米???????????????????????????????????C.?98米???????????????????????????????????D.?74米
3.同一平面内,三条不同直线的交点个数可能是( )个.
A.?1或3?????????????????B.?0、1或3???????????????????????????????C.?0、1或2???????????????????????????????D.?0、1、2或3
4.如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有(?
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.如图,在下列四组条件中,能判定AB∥CD的是(???
)
A.?∠1=∠2??????????B.?∠ABD=∠BDC????????????????????C.?∠3=∠4????????????????????D.?∠BAD+∠ABC=180°
6.如图所示,下列说法正确的是(??
)
A.?∠1和∠2是内错角??????????
B.?∠1和∠5是同位角??????????
C.?∠1和∠2是同旁内角??????????
D.?∠1和∠4是内错角
7.已知直线a、b、c相互平行,直线a与b的距离是4cm,直线b与c的距离是6cm,那么直线a与c的距离是(??
)
A.?2cm?????????????????????????????B.?5cm?????????????????????????????C.?2cm或5cm?????????????????????????????D.?2cm或10cm
8.如图,下列判断不正确的是(??
)
A.?因为∠1=∠4,所以DE∥AB????????????????????????????????????B.?因为∠2=∠3,所以AD∥EC
C.?因为∠5=∠A,所以AB∥DE????????????????????????????????????D.?因为∠ADE+∠BED=180°,所以AD∥BE
9.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.?A点??????????????????????????????????????B.?B点??????????????????????????????????????C.?C点??????????????????????????????????????D.?D点
10.在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是(?
???)
A.?(-2,6)?????????????????????????B.?(-2,0)?????????????????????????C.?(-5,3)?????????????????????????D.?(1,3)
二、填空题
11.已知∠A的两边分别平行于∠B的两边,∠B=50°,则∠A的度数为________.
12.如图,∠ABC+∠C+∠CDE=360°,直线FG分别交AB、DE于点F、G.若∠1=120°,则∠2=________°.
13.如图,已知AB∥CD,CE,AE分别平分∠ACD,∠CAB,则∠1+∠2=________.
14.一建筑物楼梯样式如图所示,经测量得出AB=3dm,BC=4dm,∠B=90°,CD=1dm,DE=1.5dm,EF=DE,AC=2AG.根据这些数据,试着计算出折线AC(即楼梯表面AJIHGFEDC)的长度为________.
15.如图,直线AB、CD被EF、EC所截,在∠1、∠2、∠3、∠4、∠5、∠6中,同位角有________个.
16.如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
17.如图,MN分别交AB、CD于点E、F,AB∥CD,∠AEM=80°,则∠DFN为________.
18.把图形进行平移,在下列特征中:
①图形的形状;②图形的位置;③线段的长度;④角的大小;⑤垂直关系;⑥平行关系.
不发生改变的有________(把你认为正确的序号都填上).
三、解答题
19.如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠1=63°,∠2=63°,且∠C=∠D.求证:∠A=∠F.
20.如图,EF∥AD,∠1=∠2,将求证AB∥DG的过程填空完整.
证明:∵EF∥AD(????????????????????
)
∴∠2=
????????????????????
(
????????????????????
)
又∵∠1=∠2(
????????????????????
)
∴∠1=∠3(
????????????????????
)
∴AB∥
????????????????????
(
????????????????????
)
四、综合题
21.如图,在平面网格中每个小正方形的边长为1.
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
22.如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
23.如图,已知AB∥CD,分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系,请从你所得四个关系中选出任意一个,说明你探究的结论的符合题意性。
结论:
(1)________;
(2)________;
(3)________;
(4)________;
(5)请从你所得四个关系中选出任意一个,说明你探究的结论的正确性。
答案
一、单选题
1.【答案】
B
【解析】【解答】解:因为直线l1//l2,
所以∠3=∠1=65°,
又因为∠3+∠2=180°,
所以∠2=180°-65=115°
故选B。
【分析】由平行线的性质可得同位角相等,即∠3=∠1,又由平角的定义可得∠3+∠2=180°,即可求出。
2.【答案】C
【解析】【解答】解:利用已知可以得出此图形可以分为横向与纵向分析,横距离等于AB,纵向距离等于(AD﹣1)×2,图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为50+(25﹣1)×2=98米,故答案为:C.
【分析】观察图形可得到横距离等于AB,纵向距离等于(AD﹣1)×2,即可求解。
3.【答案】
D
【解析】【解答】解:如图,三条直线的交点个数可能是0或1或2或3.
故选D.
【分析】根据两直线平行和相交的定义作出图形即可得解.
4.【答案】
B
【解析】【解答】解:①由∠1=∠2=70°,无法得出AB∥CD,故此选项错误;
②∵∠1=70°,
∴∠2=70°,
∵∠5=∠2=70°,
∴AB∥CD,故此选项正确;
③由∠3=110°,无法得出AB∥CD,故此选项错误;
④∵∠1=70°,
∴∠2=70°,
∵∠4=110°,
∴∠5=70°,
∴∠5=∠2=70°,
∴AB∥CD,故此选项正确;
∴其中正确的有2个.
故选:B.
【分析】直接利用邻补角的定义,结合对顶角的性质以及平行线的判定方法分析得出答案.
5.【答案】
B
【解析】【解答】A.因为∠1=∠2,而且∠1与∠2是内错角,则AD//BC,不符合;
B.因为∠ABD=∠BDC,而且∠ABD与∠BDC是内错角,则AB//CD,符合;
C.因为∠3=∠4,而且∠3与∠4是内错角,则AD//BC,不符合;
D.因为∠BAD+∠ABC=180°,而且∠BAD与∠ABC是同旁内角,则AD//BC,不符合;
【分析】根据平行线的判定理去判断:(1)同位角相等,两直线平行;(2)内错角相等,
两直线平行;(3)同旁内角互补,两直线平行.
6.【答案】C
【解析】【解答】解:A、∠1和∠2是同旁内角,故错误;
B、∠1和∠5是不是同位角,故错误;
C、∠1和∠2是同旁内角,正确;
D、∠1和∠4不是同旁内角,故错误,
故答案为:C.
【分析】利用“三线八角”的定义分别判断后即可确定正确的选项.
7.【答案】
D
【解析】【解答】当直线c在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为6cm,
∴a与c的距离=6cm﹣4cm=2cm;
当直线c不在a、b之间时,
∵a、b、c是三条平行直线,
而a与b的距离为4cm,b与c的距离为6cm,
∴a与c的距离=6cm+4cm=10cm,
综上所述,a与c的距离为2cm或10cm.
故答案为:D.
【分析】分为直线c在a、b之间或直线c不在a、b之间两种情况,然后利用平行线间的距离的意义进行求解即可.
8.【答案】C
【解析】
【分析】根据题意,结合图形,对选项一一分析,选择正确答案.
【解答】A、因为∠1=∠4,所以DE∥AB,内错角相等,两直线平行,故选项正确;
B、因为∠2=∠3,所以AD∥BE,内错角相等,两直线平行,故选项正确;
C、因为∠5与∠A,不是同位角,所以不能判定AB∥DE,故选项错误;
D、因为∠ADE+∠BED=180°,所以AD∥BE,同旁内角互补,两直线平行,故选项正确.
故选C.
【点评】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行
9.【答案】
A
【解析】【解答】解:根据垂线段最短可得:应建在A处,
故选:A.
【分析】根据垂线段最短可得答案.
10.【答案】D
【解析】【解答】将点P(-2,3)向右平移3个单位到Q点,即Q点的横坐标加3,纵坐标不变,
即Q点的坐标为(1,3),故答案为:D
【分析】根据P(-2,3)沿x轴方向向右平移3个单位则纵坐标不变,横坐标加3进行求解。
二、填空题
11.【答案】50°或130°
【解析】【解答】如图:∠B=50°或130°;故填50°或130°.
【分析】根据题意得到两种图形,由∠A的两边分别平行于∠B的两边,得到一种是∠A由∠B平移得到,故∠A=∠B;另一种是∠A与∠B是同旁内角;根据两直线平行,同旁内角互补,得到∠A的度数.
12.【答案】
60
【解析】【解答】解:过C作MC∥AB,∴∠B+∠BCM=180°.
∵∠ABC+∠BCD+∠CDE=360°,∴∠MCD+∠D=180°,∴MC∥ED,∴AB∥ED,∴∠AFG+∠2=180°.
∵∠1=120°,∴∠AFG=120°,∴∠2=180°-120°=60°.
故答案为:60.
【分析】过C作MC∥AB,根据二直线平行,同旁内角互补得出∠B+∠BCM=180°,从而根据等式的性质得出∠MCD+∠D=180°,根据同旁内角互补,两直线平行得出MC∥ED,根据平行于同一直线的两条直线互相平行得出AB∥ED,根据二直线平行,同旁内角互补得出∠AFG+∠2=180°,根据对顶角相等得出∠AFG=120°,从而即可算出答案。
13.【答案】
90°
【解析】【解答】解:∵CE、AE分别平分∠ACD、∠CAB,
∴∠1=∠DCE=∠ACD,∠2=∠BAE=∠CAB,
∴∠ACD=2∠1,∠CAB=2∠2,
又∵AB∥CD,
∴∠CAB+∠ACD=180°,
∴2∠2+2∠1=180°,
∴∠2+∠1=90°.
故答案为:90°.
【分析】根据角平分线定义得∠ACD=2∠1,∠CAB=2∠2,再由平行线性质得∠CAB+∠ACD=180°,代入、计算即可得出答案.
14.【答案】7dm
【解析】【解答】解:
由图可知:JI=AM,HG=MN,FE=NZ,CD=ZB,
AJ=BX,HI=XY,GF=YP,ED=PC,
∴计算出折线AC=(AJ+IH+GF+ED)+(JI+HG+EF+DC)=AB+BC=3+4=7(dm).
【分析】利用平移的性质,可得出折线AC的长就是AB+BC的值。
15.【答案】3
【解析】【解答】解:∠1与∠5是同位角,∠4与∠6是同位角,∠2与∠4是同位角,故答案为:3.
【分析】根据同位角的特点:两个角都在第三条直线的同旁,又分别处在被截的两条直线同侧的位置的角,呈“F”型,即可得出答案。
16.【答案】900
【解析】【解答】分别过E点,F点,G点,H点作
?平行于AB,
同旁内角,把这六个角转化一下,可得有5个180°的角,
∴180×5=900°.
【分析】分别过E点,F点,G点,H点作
l
1
,
l
2
,
l
3
,
l
4
?平行于AB,根据平行线的判定定理得出
l
1?∥
l
2?∥
l
3?∥
l
4?
∥AB∥CD
,再根据二直线平行同旁内角互补把这六个角转化一下,可得有5个180°的角,从而得出答案。
17.【答案】
80°
【解析】【解答】解:∵∠AEM=80°,
∴∠AEM=∠BEN=80°
∵AB∥CD
∴∠BEN=∠DFN=80°
故答案为:80°
【分析】根据对顶角相等求出∠BEN的度数,再根据平行线的性质证得∠BEN=∠DFN,就可得出答案。
18.【答案】①③④⑤⑥
【解析】【解答】解:由图形平移的性质,知图形在平移时,其特征不发生改变的有①③④⑤⑥.
故答案为:①③④⑤⑥.
【分析】根据平移的性质直接判断即可.
三、解答题
19.【答案】
证明:∵∠1=∠DMF,∠1=∠2=63°,
∴∠DMF=∠2,
∴DB∥CE,
∴∠C=∠DBA,
∵
∠C=∠D
,
∴∠DBA=∠D,
∴DF∥AC,
∴
∠A=∠F.
【解析】【分析】根据同位角相等两直线平行,可得DB∥CE,由两直线平行同位角相等可得∠C=∠DBA,利用内错角相等两直线平行可得
DF∥AC,最后根据两直线平行内错角相等,可得
∠A=∠F.
20.【答案】
已知;∠3;两直线平行,同位角相等;已知;等量代换;DG;内错角相等,两直线平行
【解析】【解答】证明:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等)
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥DG(内错角相等,两直线平行)
【分析】此题根据平行线的性质、判定直接完成填空.两条直线平行,则同位角相等,内错角相等,同旁内角互补;反之,同位角相等,内错角相等,同旁内角互补,则两直线平行.
四、综合题
21.【答案】(1)解:将线段AB向右平移3个小格(向下平移4
个小格),再向下平移4个小格(向右平移3个小格),
得线段CD
(2)解:将线段BD向左平移3个小格(向下平移1个小格),再向下平移1个小格(向左平移3个小格),得到线段AC
【解析】【分析】在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
22.【答案】(1)解:∵AD∥BC,∠B=60
∴∠1=∠B=60°
∵∠1=∠C,
∴∠C=∠B=60°
(2)解:DE∥AB,理由如下:
∵AD∥BC,
∴∠C+∠ADC?=180°
∴∠ADC=180°-∠C=120°
∵DE是∠ADC的平分线,
∴∠ADE=
∠BDC=60°
∵∠1=∠B=60°
∴∠1=∠ADE.
∴DE∥AB.
【解析】【分析】(1)由AD//BC
,可知∠1=∠B=,又因为∠1=∠C,所以可知∠C=;
(2)同样由AD//BC
,同旁内角互补,可知∠ADC=,又因为DE平分∠ADC,结合三角形内角和定理可知,∠EDC=∠DEC=,所以∠B=∠DEC,AB//DE
.
23.【答案】
(1)∠APC+∠PAB+∠PCD=180°
(2)∠APC=∠PAB+∠PCD
(3)∠APC=∠PCD-∠PAB
(4)∠APC=∠PAB-∠PCD
(5)解:选择(1)
如图,过点P作PE∥CD则∠CPE+∠PCD=180°
∵CD∥AB
∴PE∥AB
∴∠APE+∠PAB=180°
∴∠APC+∠PAB+∠PCD=180°
【解析】【分析】根据两平行线间夹折线的解决方法:过折点做一条直线的平行线,证明它与另一条直线也平行,即可得到三条互相平行的直线,利用平行线的性质转化角的关系即可。
/
