求函数值域同步习题
图片预览
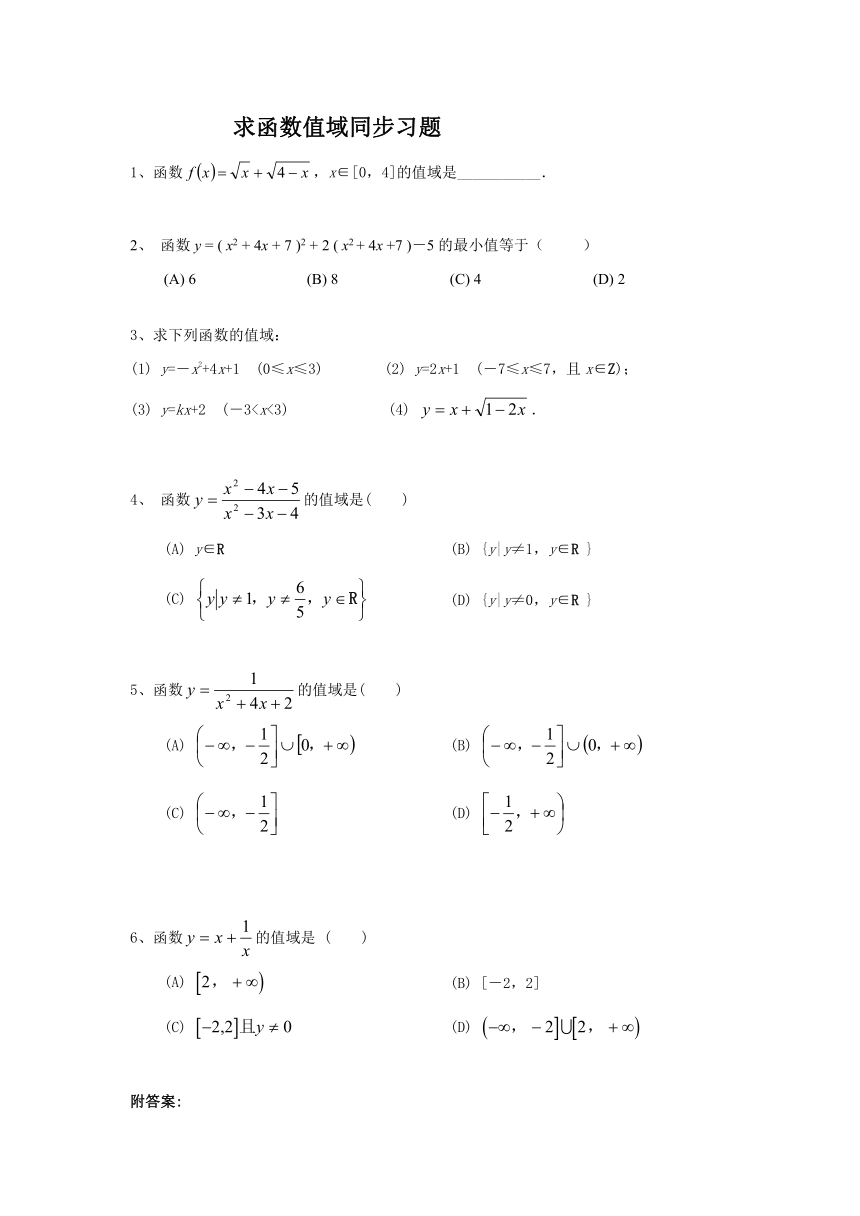
文档简介
求函数值域同步习题
1、函数,x∈[0,4]的值域是___________.
2、 函数y = ( x2 + 4x + 7 )2 + 2 ( x2 + 4x +7 )-5的最小值等于( )
(A) 6 (B) 8 (C) 4 (D) 2
3、求下列函数的值域:
(1) y=-x2+4x+1 (0≤x≤3) (2) y=2x+1 (-7≤x≤7,且x∈Z);
(3) y=kx+2 (-34、 函数的值域是( )
(A) y∈R (B) {y|y≠1,y∈R }
(C) (D) {y|y≠0,y∈R }
5、函数的值域是( )
(A) (B)
(C) (D)
6、函数的值域是 ( )
(A) (B) [-2,2]
(C) (D)
附答案:
1、答案:
分析:
∵ x∈[0,4],∴ ,
∴ .
又 4 ≤ y2 ≤ 4 + (x + 4-x) = 8
∴ .
2、答案:C
分析:
令t = x2 + 4x + 7≥3.转化为求y = f ( t ) = t2 + 2t-5(t≥3)的最小值.
3、答案:
(1) {y|1≤y≤5} (2) {y|-13≤y≤15,y∈Z}
(3) k=0时,y∈{2};k>0时,y∈{y|-3k+2(4)
分析:
设 t≥0转化为求 (t≥0)的值域
4、答案:C
分析:
是求复合函数值域问题.基本方法是由定义域出发由里往外逐层求出每层函数的值域,直至最外层的函数值域即所求,
,
如果某层函数值域易求,也可由此往外逐层求出.
5、 答案:B
分析:
是求复合函数值域问题.基本方法是由定义域出发由里往外逐层求出每层函数的值域,直至最外层的函数值域即所求,如果某层函数值域易求,也可由此往外逐层求出.
∵ .又.
∴ .
6、 答案:D
1、函数,x∈[0,4]的值域是___________.
2、 函数y = ( x2 + 4x + 7 )2 + 2 ( x2 + 4x +7 )-5的最小值等于( )
(A) 6 (B) 8 (C) 4 (D) 2
3、求下列函数的值域:
(1) y=-x2+4x+1 (0≤x≤3) (2) y=2x+1 (-7≤x≤7,且x∈Z);
(3) y=kx+2 (-3
(A) y∈R (B) {y|y≠1,y∈R }
(C) (D) {y|y≠0,y∈R }
5、函数的值域是( )
(A) (B)
(C) (D)
6、函数的值域是 ( )
(A) (B) [-2,2]
(C) (D)
附答案:
1、答案:
分析:
∵ x∈[0,4],∴ ,
∴ .
又 4 ≤ y2 ≤ 4 + (x + 4-x) = 8
∴ .
2、答案:C
分析:
令t = x2 + 4x + 7≥3.转化为求y = f ( t ) = t2 + 2t-5(t≥3)的最小值.
3、答案:
(1) {y|1≤y≤5} (2) {y|-13≤y≤15,y∈Z}
(3) k=0时,y∈{2};k>0时,y∈{y|-3k+2
分析:
设 t≥0转化为求 (t≥0)的值域
4、答案:C
分析:
是求复合函数值域问题.基本方法是由定义域出发由里往外逐层求出每层函数的值域,直至最外层的函数值域即所求,
,
如果某层函数值域易求,也可由此往外逐层求出.
5、 答案:B
分析:
是求复合函数值域问题.基本方法是由定义域出发由里往外逐层求出每层函数的值域,直至最外层的函数值域即所求,如果某层函数值域易求,也可由此往外逐层求出.
∵ .又.
∴ .
6、 答案:D
