人教版高中物理必修2第7章第2节万有引力定律课件(共30张PPT)
文档属性
| 名称 | 人教版高中物理必修2第7章第2节万有引力定律课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-29 05:55:42 | ||
图片预览










文档简介
(共30张PPT)
万有引力定律
新知讲解
1、伽利略:
认为行星的运动是由“惯性”自行维持的。
一、科学家们的探索之路
2、开普勒
行星的运动是受到了来自太阳的类似于磁力的作用
,与距离成反比。
3、笛卡尔
认为在行星的周围有旋转的物质作用在行星上,使得行星绕太阳运动
新知讲解
下面我们根据牛顿运动定律及开普勒行星运动定律来讨论太阳与行星间的引力。
4、胡克:认为行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
5、牛顿:认为以任何方式改变速度(包括改变速度的方向)都需要力。这就是说,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。
新知讲解
二、行星与太阳间的引力
1、简化模型:行星轨道按照“圆”来处理;
太阳
行星
v
行星做匀速圆周运动时,受到一个指向圆心(太阳)的引力提供了向心力,太阳与行星间引力的方向沿着二者的连线。
F
F’
新知讲解
问题:设行星的质量为
m,速度为
v,行星与太阳间的距离为
r,周期为T,请推导太阳对行星的引力F。
mv2
r
F=
——
解:行星绕太阳做匀速圆周运动的向心力为:
①
v
=
——
2πr
T
周期为T与线速度为v的关系:
②
F
=
——
4π2mr
T2
②代入①得:
③
2、太阳和行星之间的引力
新知讲解
上式等号右边4π2k为常量,太阳对行星的引力跟行星的质量成正比,与行星、太阳距离的二次方成反比:即
F
∝m/r2
。
由开普勒第三定律:
=k
得:T2
=
,
——
r3
T2
——
r3
k
F
=
4π2k——
m
r2
同理行星对太阳的引力跟太阳的质量成正比,与行星、太阳距离的二次方成反比:即:F′
∝M/r2
代入③得:
新知讲解
由牛顿第三定律知F和
F′的大小相等,因此太阳和行星之间的引力与行星和太阳的质量成正比与距离的二次方成反比
F
∝——
Mm
r2
写成等式就是:
F
=G
——
Mm
r2
式中量
G
与太阳、行星都没有关系。太阳与行星间引力的方向沿着二者的连线。
至此,牛顿一直是在已有的观测结果和理论引导下进行推测和分析,观测结果仅对“行星绕太阳运动”成立,这还不是万有引力定律。
新知讲解
三、月—地检验
思考:地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗?
这种力与地球对树上苹果的吸引力也是同一种性质的力吗?
新知讲解
1.月—地检验的目的:检验维持月球绕地球运动的力与使物体下落的力是同一种性质力,都遵从“平方反比”的规律。
2.月—地检验的推导
假设地球与月球间的作用力与太阳与行星间的作用力是同一种力,
为了验证地面上的重力与地球吸引月球、太阳吸引行星的力是同一性质的力,遵守同样的规律,牛顿还做了著名的“月-地”检验。
新知讲解
F
=
G___________
m月
m地
r2
则应该满足:
F
根据牛顿第二定律:
a月=
——
m月
=G______
m地
r2
(r
是地球中心与月球中心的距离
)
①
(
R
是地球中心与苹果间的距离
)
假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度
=G______
m地
R2
a苹
②
——
=
——
R
的
60
倍,所以:
①/②可得:
a月
a苹
R2
r2
由于月球与地球中心的距离
r
约为地球半径
——
=
——
a月
a苹
602
1
新知讲解
已知自由落体加速度
g
为
9.8
m/s2
,月球中心距离地球中心的距离为3.8×108
m,月球公转周期为
27.3
d,约
2.36×106
s,
根据这些数据,能否验证前面的假设?
思考讨论
求:——
a月
a苹
解:a月=(
——)2r=(
————)2
×
3.8×108
m/s2
≈2.69×10-3
m/s2
2π
T
2×3.14
2.36×106
——
=
2.7×10-4
≈
a月
a苹
——
602
1
新知讲解
这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律。
四、万有引力定律
1、定律表述:自然界中任何两个物体都是互相吸引的,引力的方向在它们的连线上,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比.
新知讲解
F
=
G___________
m1
m2
r2
2、公式表达:
(1)m1和m2表示两个物体的质量单位用千克(kg);
(2)r表示它们的距离单位用米(m)。力的单位用牛(N)
(3)G
是比例系数,叫作引力常量,适用于任何两个物体。
自然界中任何两个物体都是互相吸引的,所以说:万有引力具有相互性、普遍性。另外万有引力还具有宏观性。
3、对万有引力的理解
新知讲解
(1)可视为质点的两物体间的引力;
4、适用条件
r
指质点和球心间的距离。
r
(2)两质量均匀分布的球体间的引力。
r指的是两球心间的距离。
r
(3)一质量均匀分布的球体和一质点间的引力。
新知讲解
五、引力常量的测定
1789年,即在牛顿发现万有引力定律一百多年以后,英国物理学家卡文迪许,在实验室里通过测量几个铅球之间的万有引力,比较准确地得出了
G
的数值。
1、引力常量G
的数值
目前推荐的引力常量G标准值
:G
=
6.672
59
×
10
-11N·
m2/kg2,通常取:G=6.67×10-11
N·m2/kg2
知识拓展
1、实验原理
力矩平衡,即引力矩=扭转力矩。
2、科学方法:放大法
3、科学思想:等效的思想。
(1)扭秤装置把微小力转变成力矩来反映。
(2)扭转角度(微小形变)通过光标的移动来反映。
卡文迪许实验
动画演示:卡文迪许实验
新知讲解
既然自然界中任何两个物体都是互相吸引的,为什么我们感觉不到周围物体的引力呢?
为什么说万有引力具有宏观性?
计算:两个质量为60kg,相距1m的物体之间的引力?
=2.4012×10-7N
此力不到一粒芝麻重的几千分之一所以根本感觉不到它的存在。
解:
思考讨论1
计算:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg,日地之间的距离为R=1.5×1011m请计算:太阳与地球之间的万有引力又是多大呢?
新知讲解
=
—————————————=
3.5×1022(N)
6.67×10-11×
2.0×1030
×6.0×1024
(1.5×1011)2
太阳与地球之间的万有引力的大小能竟能拉断直径为9000km的钢柱,非常巨大。
解:
通常情况下,万有引力非常小,只有质量巨大的星球间或天体与附近的物体间,它的存在才有实际的物理意义所以说万有引力还具有宏观性。
新知讲解
一个篮球的质量为
0.6
kg,它所受的重力有多大?试估算操场上相距
0.5
m
的两个篮球之间的万有引力。
解:G=mg=0.6×9.8N=5.88N
思考讨论2
F
=
G___________=
6.67×10-11
____________≈
9.6
×10-11N
m1
m2
r2
0.6×0.6
0.52
可见两个篮球间万有引力比重力小的多,人们根本无法察觉到,可忽略不计。
新知讲解
2、引力常量物理意义:引力常量在数值上等于两个质量都是1
kg的质点相距1
m时的相互吸引力。
3、引力常量测定的意义
(1)卡文迪许利用扭秤装置通过改变小球的质量和距离,得到了G的数值,验证了万有引力定律的正确性。
(2)引力常量的确定使万有引力定律能够进行定量的计算,显示出真正的实用价值。
新知讲解
科学漫步
牛顿的科学生涯
阅读回答下面问题:
1、简述牛顿的科学生涯。
2、说一说牛顿在前人的基础上形成了比较全面的科学方法是什么?
3、在科学研究方面我们应该学习牛顿的哪些品质?
课堂练习
1.火星轨道半径是地球轨道半径的a倍,火星质量约为地球质量的b倍,那么火星与太阳之间的引力约为地球与太阳之间引力的______倍。
2.在牛顿发现太阳与行星间的引力过程中,得出太阳对行星的引力表达式后推出行星对太阳的引力表达式,是一个很关键的论证步骤,这一步骤采用的论证方法是( )
A.研究对象的选取
B.理想化过程
C.控制变量法
D.等效法
D
课堂练习
3、一名宇航员来到一个星球上,如果该星球的质量是地球质量的一半,它的直径也是地球直径的一半,那么这名宇航员在该星球上所受的万有引力大小是他在地球上所受万有引力大小的( )
0.25倍
B.
0.5倍
C.
2.0倍
D.
4.0倍
C
课堂练习
4.
4月30日,西昌卫星发射中心发射了一圆轨道卫星,其轨道半径为2.8×107m,它与另一颗同质量的同步轨道卫星(轨道半径为
4.2×107m)相比(
)
A.?向心加速度较小??????????????
B.?周期较大??????????????????????
C.?线速度较大??????????????????????
D.?机械能较大
C
1.“嫦娥一号”和“嫦娥二号”卫星相继完成了对月球的环月飞行,标志着我国探月工程的第一阶段已经完成.设“嫦娥二号”卫星环绕月球的运动为匀速圆周运动,它距月球表面的高度为h,已知月球的质量为M、半径为R,引力常量为G,则卫星绕月球运动的向心加速度a=________,线速度v=________.
拓展提高
拓展提高
2.对于万有引力定律的表达式F=
,下面说法中正确的是( )
A.当r趋近于零时,万有引力趋于无穷大
B.公式中G为引力常量,它是由实验测得的,而不是人为规定的
C.若m1>m2,则m1受到的引力大于m2受到的引力
D.m1与m2受到的引力大小相等,是一对平衡力
B
拓展提高
3.最近,科学家在望远镜中看到太阳系外某一恒星有一行星,并测得它围绕该恒星运动一周所用的时间为1200年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个数据可以求出的量有(
)
恒星质量与太阳质量之比
B.
恒星密度与太阳密度之比
C.
行星质量与地球质量之比
D.
行星运行速度与地球公转速度之比
AD
课堂总结
1、万有引力定律公式
F
=
G___________
m1
m2
r2
2、适用条件
(1)适用于质点间引力大小的计算。
(2)
对于可视为质点的物体间的引力求解也可以利用万有引力公式。
(3)
当研究的物体不能看成质点时,可以把物体假想分割成无数质点,求分力,再求合力。
G=6.67×10-11
N·m2/kg2
板书设计
一、科学家们的探索之路
二、行星与太阳间的引力
太阳和行星之间的引力与行星和太阳的质量成正比与距离的二次方成反比。
三、月—地检验
太阳与行星间、地球与月球间、地球与地面物体间的力是同一种性质的力。
五、引力常量的测定
卡文迪许通过实验测出:G=6.67×10-11
N?m2/kg2
意义:证明了万有引力的存在;使万有引力定律有了真正的实用价值。
板书设计
四、万有引力定律
F
=
G___________
m1
m2
r2
普遍性、相互性、宏观性
万有引力定律
新知讲解
1、伽利略:
认为行星的运动是由“惯性”自行维持的。
一、科学家们的探索之路
2、开普勒
行星的运动是受到了来自太阳的类似于磁力的作用
,与距离成反比。
3、笛卡尔
认为在行星的周围有旋转的物质作用在行星上,使得行星绕太阳运动
新知讲解
下面我们根据牛顿运动定律及开普勒行星运动定律来讨论太阳与行星间的引力。
4、胡克:认为行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
5、牛顿:认为以任何方式改变速度(包括改变速度的方向)都需要力。这就是说,使行星沿圆或椭圆运动,需要指向圆心或椭圆焦点的力,这个力应该就是太阳对它的引力。
新知讲解
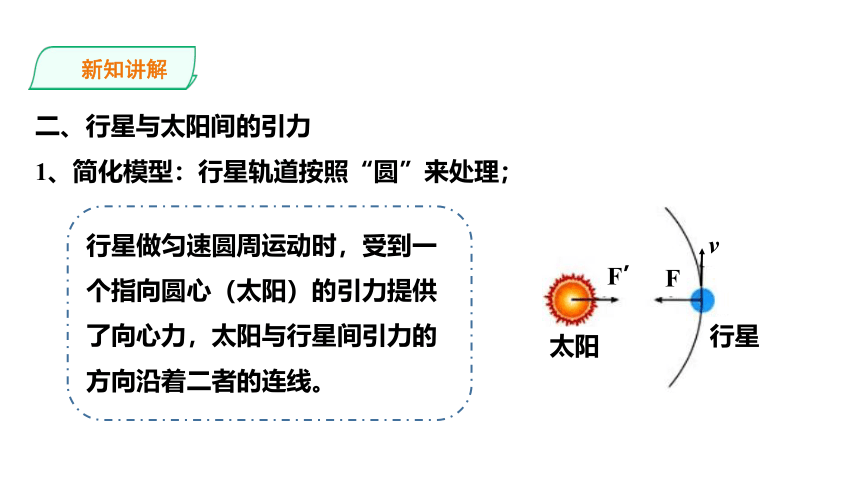
二、行星与太阳间的引力
1、简化模型:行星轨道按照“圆”来处理;
太阳
行星
v
行星做匀速圆周运动时,受到一个指向圆心(太阳)的引力提供了向心力,太阳与行星间引力的方向沿着二者的连线。
F
F’
新知讲解
问题:设行星的质量为
m,速度为
v,行星与太阳间的距离为
r,周期为T,请推导太阳对行星的引力F。
mv2
r
F=
——
解:行星绕太阳做匀速圆周运动的向心力为:
①
v
=
——
2πr
T
周期为T与线速度为v的关系:
②
F
=
——
4π2mr
T2
②代入①得:
③
2、太阳和行星之间的引力
新知讲解
上式等号右边4π2k为常量,太阳对行星的引力跟行星的质量成正比,与行星、太阳距离的二次方成反比:即
F
∝m/r2
。
由开普勒第三定律:
=k
得:T2
=
,
——
r3
T2
——
r3
k
F
=
4π2k——
m
r2
同理行星对太阳的引力跟太阳的质量成正比,与行星、太阳距离的二次方成反比:即:F′
∝M/r2
代入③得:
新知讲解
由牛顿第三定律知F和
F′的大小相等,因此太阳和行星之间的引力与行星和太阳的质量成正比与距离的二次方成反比
F
∝——
Mm
r2
写成等式就是:
F
=G
——
Mm
r2
式中量
G
与太阳、行星都没有关系。太阳与行星间引力的方向沿着二者的连线。
至此,牛顿一直是在已有的观测结果和理论引导下进行推测和分析,观测结果仅对“行星绕太阳运动”成立,这还不是万有引力定律。
新知讲解
三、月—地检验
思考:地球绕太阳运动,月球绕地球运动,它们之间的作用力是同一种性质的力吗?
这种力与地球对树上苹果的吸引力也是同一种性质的力吗?
新知讲解
1.月—地检验的目的:检验维持月球绕地球运动的力与使物体下落的力是同一种性质力,都遵从“平方反比”的规律。
2.月—地检验的推导
假设地球与月球间的作用力与太阳与行星间的作用力是同一种力,
为了验证地面上的重力与地球吸引月球、太阳吸引行星的力是同一性质的力,遵守同样的规律,牛顿还做了著名的“月-地”检验。
新知讲解
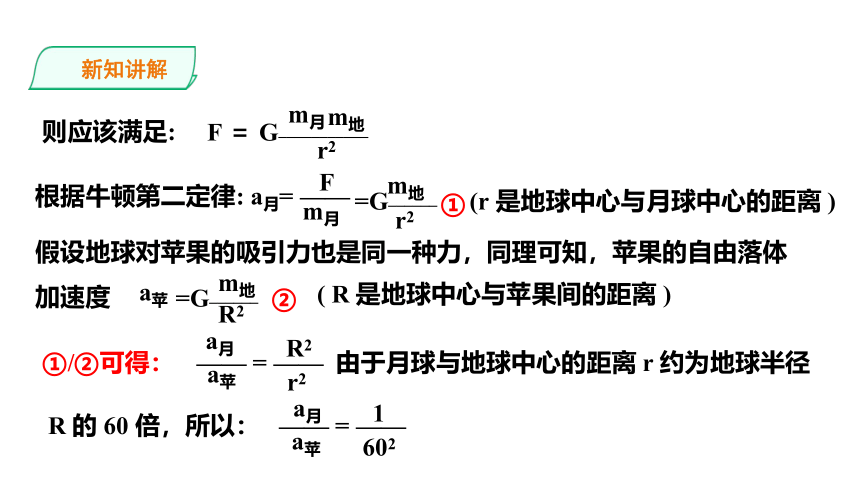
F
=
G___________
m月
m地
r2
则应该满足:
F
根据牛顿第二定律:
a月=
——
m月
=G______
m地
r2
(r
是地球中心与月球中心的距离
)
①
(
R
是地球中心与苹果间的距离
)
假设地球对苹果的吸引力也是同一种力,同理可知,苹果的自由落体加速度
=G______
m地
R2
a苹
②
——
=
——
R
的
60
倍,所以:
①/②可得:
a月
a苹
R2
r2
由于月球与地球中心的距离
r
约为地球半径
——
=
——
a月
a苹
602
1
新知讲解
已知自由落体加速度
g
为
9.8
m/s2
,月球中心距离地球中心的距离为3.8×108
m,月球公转周期为
27.3
d,约
2.36×106
s,
根据这些数据,能否验证前面的假设?
思考讨论
求:——
a月
a苹
解:a月=(
——)2r=(
————)2
×
3.8×108
m/s2
≈2.69×10-3
m/s2
2π
T
2×3.14
2.36×106
——
=
2.7×10-4
≈
a月
a苹
——
602
1
新知讲解
这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律。
四、万有引力定律
1、定律表述:自然界中任何两个物体都是互相吸引的,引力的方向在它们的连线上,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比.
新知讲解
F
=
G___________
m1
m2
r2
2、公式表达:
(1)m1和m2表示两个物体的质量单位用千克(kg);
(2)r表示它们的距离单位用米(m)。力的单位用牛(N)
(3)G
是比例系数,叫作引力常量,适用于任何两个物体。
自然界中任何两个物体都是互相吸引的,所以说:万有引力具有相互性、普遍性。另外万有引力还具有宏观性。
3、对万有引力的理解
新知讲解
(1)可视为质点的两物体间的引力;
4、适用条件
r
指质点和球心间的距离。
r
(2)两质量均匀分布的球体间的引力。
r指的是两球心间的距离。
r
(3)一质量均匀分布的球体和一质点间的引力。
新知讲解
五、引力常量的测定
1789年,即在牛顿发现万有引力定律一百多年以后,英国物理学家卡文迪许,在实验室里通过测量几个铅球之间的万有引力,比较准确地得出了
G
的数值。
1、引力常量G
的数值
目前推荐的引力常量G标准值
:G
=
6.672
59
×
10
-11N·
m2/kg2,通常取:G=6.67×10-11
N·m2/kg2
知识拓展
1、实验原理
力矩平衡,即引力矩=扭转力矩。
2、科学方法:放大法
3、科学思想:等效的思想。
(1)扭秤装置把微小力转变成力矩来反映。
(2)扭转角度(微小形变)通过光标的移动来反映。
卡文迪许实验
动画演示:卡文迪许实验
新知讲解
既然自然界中任何两个物体都是互相吸引的,为什么我们感觉不到周围物体的引力呢?
为什么说万有引力具有宏观性?
计算:两个质量为60kg,相距1m的物体之间的引力?
=2.4012×10-7N
此力不到一粒芝麻重的几千分之一所以根本感觉不到它的存在。
解:
思考讨论1
计算:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg,日地之间的距离为R=1.5×1011m请计算:太阳与地球之间的万有引力又是多大呢?
新知讲解
=
—————————————=
3.5×1022(N)
6.67×10-11×
2.0×1030
×6.0×1024
(1.5×1011)2
太阳与地球之间的万有引力的大小能竟能拉断直径为9000km的钢柱,非常巨大。
解:
通常情况下,万有引力非常小,只有质量巨大的星球间或天体与附近的物体间,它的存在才有实际的物理意义所以说万有引力还具有宏观性。
新知讲解
一个篮球的质量为
0.6
kg,它所受的重力有多大?试估算操场上相距
0.5
m
的两个篮球之间的万有引力。
解:G=mg=0.6×9.8N=5.88N
思考讨论2
F
=
G___________=
6.67×10-11
____________≈
9.6
×10-11N
m1
m2
r2
0.6×0.6
0.52
可见两个篮球间万有引力比重力小的多,人们根本无法察觉到,可忽略不计。
新知讲解
2、引力常量物理意义:引力常量在数值上等于两个质量都是1
kg的质点相距1
m时的相互吸引力。
3、引力常量测定的意义
(1)卡文迪许利用扭秤装置通过改变小球的质量和距离,得到了G的数值,验证了万有引力定律的正确性。
(2)引力常量的确定使万有引力定律能够进行定量的计算,显示出真正的实用价值。
新知讲解
科学漫步
牛顿的科学生涯
阅读回答下面问题:
1、简述牛顿的科学生涯。
2、说一说牛顿在前人的基础上形成了比较全面的科学方法是什么?
3、在科学研究方面我们应该学习牛顿的哪些品质?
课堂练习
1.火星轨道半径是地球轨道半径的a倍,火星质量约为地球质量的b倍,那么火星与太阳之间的引力约为地球与太阳之间引力的______倍。
2.在牛顿发现太阳与行星间的引力过程中,得出太阳对行星的引力表达式后推出行星对太阳的引力表达式,是一个很关键的论证步骤,这一步骤采用的论证方法是( )
A.研究对象的选取
B.理想化过程
C.控制变量法
D.等效法
D
课堂练习
3、一名宇航员来到一个星球上,如果该星球的质量是地球质量的一半,它的直径也是地球直径的一半,那么这名宇航员在该星球上所受的万有引力大小是他在地球上所受万有引力大小的( )
0.25倍
B.
0.5倍
C.
2.0倍
D.
4.0倍
C
课堂练习
4.
4月30日,西昌卫星发射中心发射了一圆轨道卫星,其轨道半径为2.8×107m,它与另一颗同质量的同步轨道卫星(轨道半径为
4.2×107m)相比(
)
A.?向心加速度较小??????????????
B.?周期较大??????????????????????
C.?线速度较大??????????????????????
D.?机械能较大
C
1.“嫦娥一号”和“嫦娥二号”卫星相继完成了对月球的环月飞行,标志着我国探月工程的第一阶段已经完成.设“嫦娥二号”卫星环绕月球的运动为匀速圆周运动,它距月球表面的高度为h,已知月球的质量为M、半径为R,引力常量为G,则卫星绕月球运动的向心加速度a=________,线速度v=________.
拓展提高
拓展提高
2.对于万有引力定律的表达式F=
,下面说法中正确的是( )
A.当r趋近于零时,万有引力趋于无穷大
B.公式中G为引力常量,它是由实验测得的,而不是人为规定的
C.若m1>m2,则m1受到的引力大于m2受到的引力
D.m1与m2受到的引力大小相等,是一对平衡力
B
拓展提高
3.最近,科学家在望远镜中看到太阳系外某一恒星有一行星,并测得它围绕该恒星运动一周所用的时间为1200年,它与该恒星的距离为地球到太阳距离的100倍.假定该行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周,仅利用以上两个数据可以求出的量有(
)
恒星质量与太阳质量之比
B.
恒星密度与太阳密度之比
C.
行星质量与地球质量之比
D.
行星运行速度与地球公转速度之比
AD
课堂总结
1、万有引力定律公式
F
=
G___________
m1
m2
r2
2、适用条件
(1)适用于质点间引力大小的计算。
(2)
对于可视为质点的物体间的引力求解也可以利用万有引力公式。
(3)
当研究的物体不能看成质点时,可以把物体假想分割成无数质点,求分力,再求合力。
G=6.67×10-11
N·m2/kg2
板书设计
一、科学家们的探索之路
二、行星与太阳间的引力
太阳和行星之间的引力与行星和太阳的质量成正比与距离的二次方成反比。
三、月—地检验
太阳与行星间、地球与月球间、地球与地面物体间的力是同一种性质的力。
五、引力常量的测定
卡文迪许通过实验测出:G=6.67×10-11
N?m2/kg2
意义:证明了万有引力的存在;使万有引力定律有了真正的实用价值。
板书设计
四、万有引力定律
F
=
G___________
m1
m2
r2
普遍性、相互性、宏观性
