六年级上册数学课件-8 数与形人教版 (共25张PPT)
文档属性
| 名称 | 六年级上册数学课件-8 数与形人教版 (共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 07:52:01 | ||
图片预览




文档简介
(共24张PPT)
数
形
与
数量关系
空间形式
数
与
形
数 学
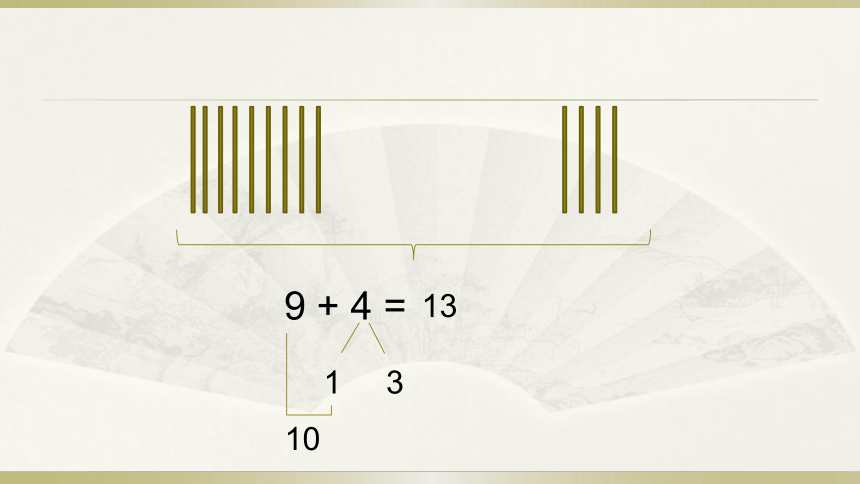
9 + 4 =
1 3
10
13
5
4
5
4
4
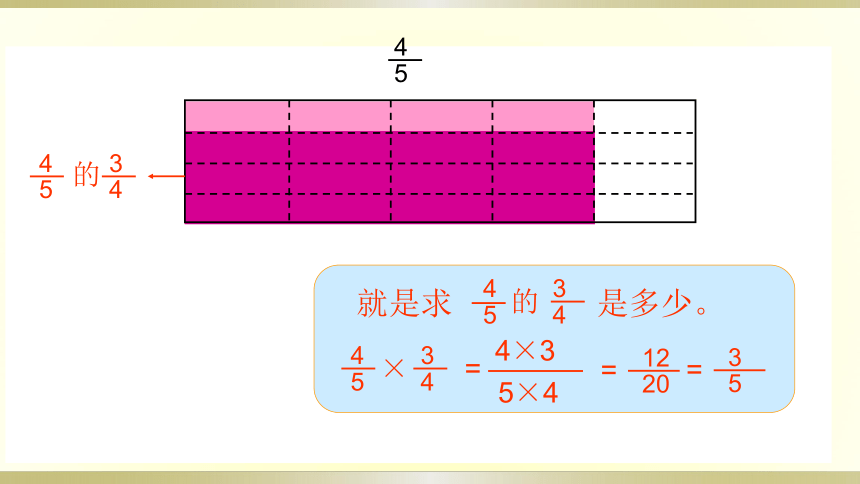
3
的
就是求 是多少。
5
4
4
3
的
5
4
4
3
× =
5×4
4×3
=
20
12
=
5
3
从1开始,
连续奇数和,
正好是这些加数
个数的平方。
1
3
5
7
9
1+3
1+3+5
1+3+5+7
1+3+5+7+9
1+3+5+7+9+…=( )
n个
n
2
1
= 1
2
= 2
2
= 3
2
= 4
2
= 5
2
1+3+5+7+9+11
= 6
2
11
…
…
练习1:
1+3+5+7+9+11=( )
62
1+3+5+7+9+11+13=( )
72
练习1:
( ) = 152
1+3+5+7+9+11+13+15+17+19+21+23+25+27+29
练习1:
运用例1得到的结论,能直接算出下面式子的结果吗?
练习2:
11+13+15+17+19 =( )
10 - 5
2
2
= ( )
75
运用例1得到的结论,能直接算出下面式子的结果吗?
2+4+6+8+10+12+14+16+18+20=( )
102+10
n2+n
练习2:
规律:从2开始的n个连续偶数的和等于 。
练习3:
一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人....照这样,9张桌子并成一排可以坐多少人?如果一共有30个人需要多少张桌子
.....
2+2×2=
2+2×3=
2+2×9=20(人)
(30-2)÷2=14(张)
答:9张桌子并成一排可以坐20人,如果一共有30个人需要14张桌子。
4人
2+2×1=
6人
8人
5-2=3(个)
返回
数形结合
乘法算式: 或
4 个 3
3+3+3+3=12(个)
4×3=12(个)
3×4=12(个)
数形结合
加法算式:
植树问题
数形结合
两边都种:
植树的棵数=间隔数+1
一边种:
两边都不种:
植树的棵数=间隔数
植树的棵数=间隔数-1
封闭图形的棵数
=间隔数
我国著名数学家华罗庚说:
数形结合百般好,
隔离分家万事休。
红色:
蓝色:
3
1
8
2
10
12
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
照这样画下去:
第6个图形有_____个红色小正方形和_____个蓝色小正方形。
第10个图形有_______个红色小正方形和______个蓝色小正方形。
第n个图形有______个红色小正方形和______个蓝色小正方形。
4
14
①
④
②
③
6
18
10
26
n
①
④
②
③
n
×
2
+
6
数
形
与
数量关系
空间形式
数
与
形
数 学
9 + 4 =
1 3
10
13
5
4
5
4
4
3
的
就是求 是多少。
5
4
4
3
的
5
4
4
3
× =
5×4
4×3
=
20
12
=
5
3
从1开始,
连续奇数和,
正好是这些加数
个数的平方。
1
3
5
7
9
1+3
1+3+5
1+3+5+7
1+3+5+7+9
1+3+5+7+9+…=( )
n个
n
2
1
= 1
2
= 2
2
= 3
2
= 4
2
= 5
2
1+3+5+7+9+11
= 6
2
11
…
…
练习1:
1+3+5+7+9+11=( )
62
1+3+5+7+9+11+13=( )
72
练习1:
( ) = 152
1+3+5+7+9+11+13+15+17+19+21+23+25+27+29
练习1:
运用例1得到的结论,能直接算出下面式子的结果吗?
练习2:
11+13+15+17+19 =( )
10 - 5
2
2
= ( )
75
运用例1得到的结论,能直接算出下面式子的结果吗?
2+4+6+8+10+12+14+16+18+20=( )
102+10
n2+n
练习2:
规律:从2开始的n个连续偶数的和等于 。
练习3:
一张桌子坐4人,两张桌子并起来坐6人,三张桌子并起来坐8人....照这样,9张桌子并成一排可以坐多少人?如果一共有30个人需要多少张桌子
.....
2+2×2=
2+2×3=
2+2×9=20(人)
(30-2)÷2=14(张)
答:9张桌子并成一排可以坐20人,如果一共有30个人需要14张桌子。
4人
2+2×1=
6人
8人
5-2=3(个)
返回
数形结合
乘法算式: 或
4 个 3
3+3+3+3=12(个)
4×3=12(个)
3×4=12(个)
数形结合
加法算式:
植树问题
数形结合
两边都种:
植树的棵数=间隔数+1
一边种:
两边都不种:
植树的棵数=间隔数
植树的棵数=间隔数-1
封闭图形的棵数
=间隔数
我国著名数学家华罗庚说:
数形结合百般好,
隔离分家万事休。
红色:
蓝色:
3
1
8
2
10
12
下面每个图中各有多少个红色小正方形和多少个蓝色小正方形?
照这样画下去:
第6个图形有_____个红色小正方形和_____个蓝色小正方形。
第10个图形有_______个红色小正方形和______个蓝色小正方形。
第n个图形有______个红色小正方形和______个蓝色小正方形。
4
14
①
④
②
③
6
18
10
26
n
①
④
②
③
n
×
2
+
6
