1.3 勾股定理的应用课件(共27张PPT)
文档属性
| 名称 | 1.3 勾股定理的应用课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 00:00:00 | ||
图片预览



文档简介
北师大版八年级上册
第一章
勾股定理
1.3 勾股定理的应用
一、情景导入
B
A
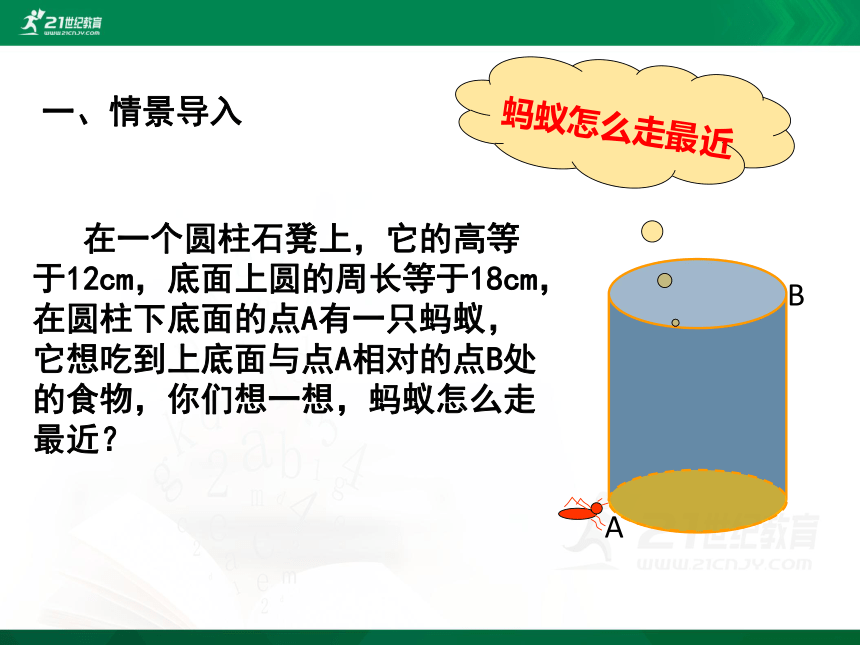
蚂蚁怎么走最近
在一个圆柱石凳上,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,你们想一想,蚂蚁怎么走最近?
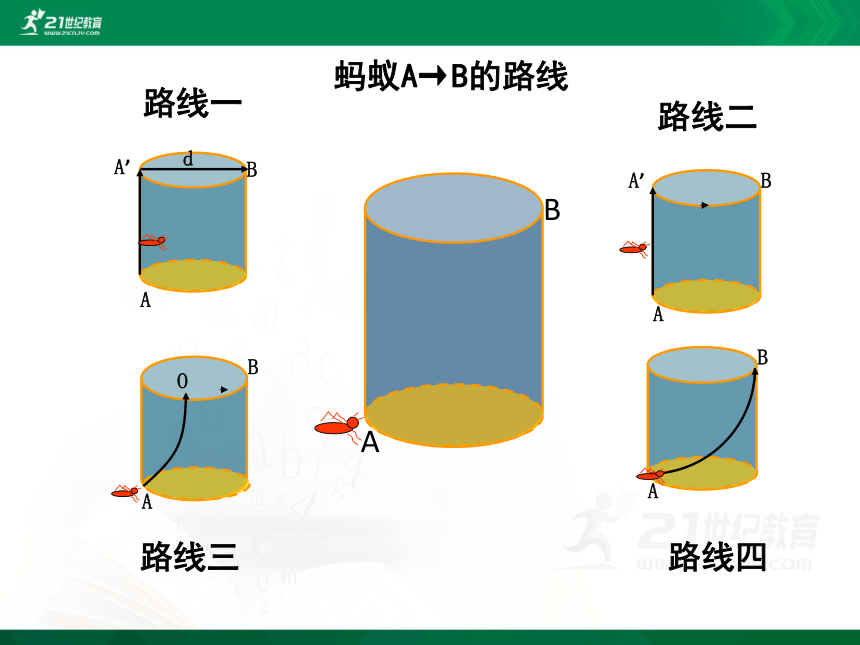
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
B
A
路线一
路线二
路线三
路线四
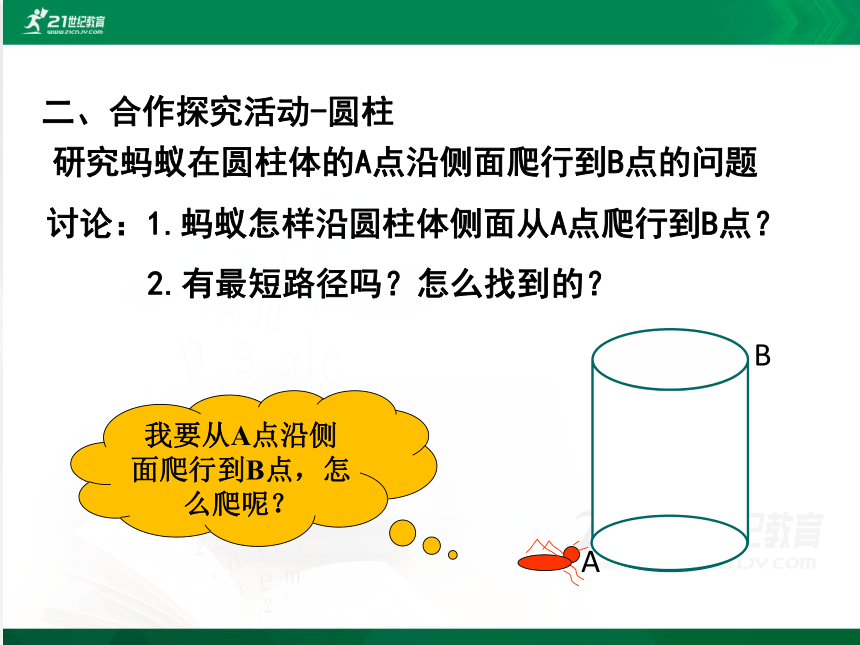
研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题
讨论:1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点?
2.有最短路径吗?怎么找到的?
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?
二、合作探究活动-圆柱
A
B
A’
B
A
A’
r
O
h
侧面展开图
C
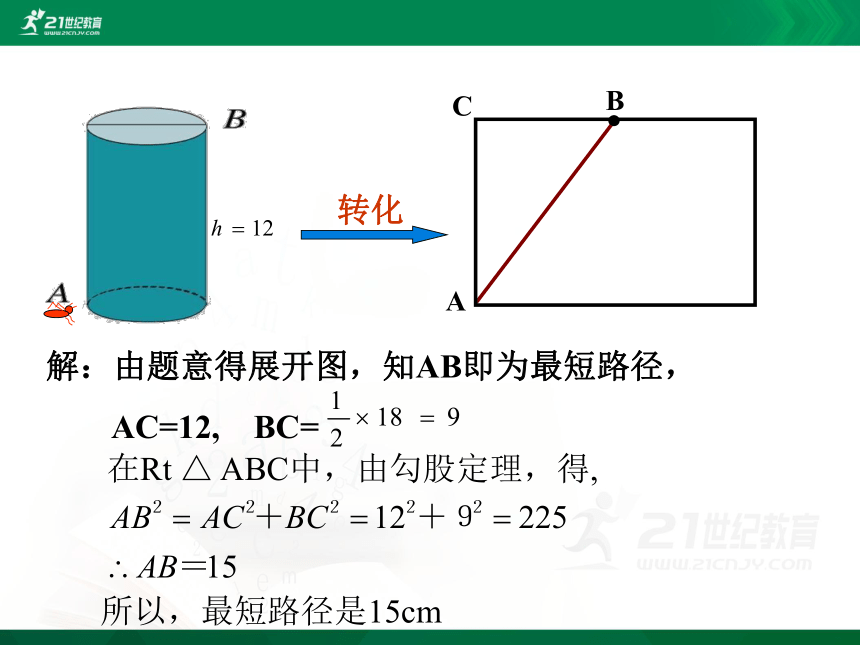
解:由题意得展开图,知AB即为最短路径,
AC=12, BC=
所以,最短路径是15cm
转化
B
A
在Rt △ ABC中,由勾股定理,得,
方法总结:
—侧面展开图中两点之间的连线段最短
A
B
A’
B
A
A’
r
O
h
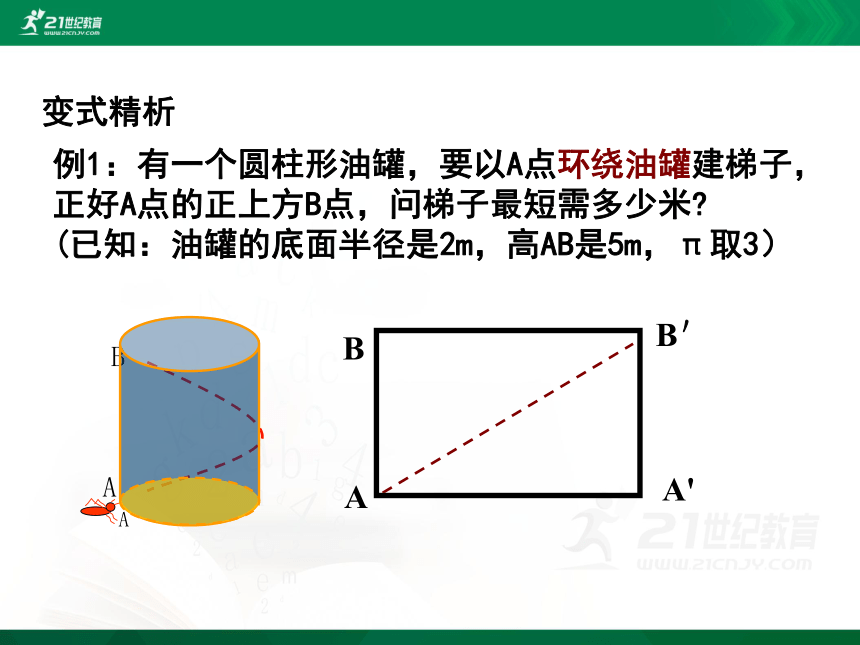
例1:有一个圆柱形油罐,要以A点环绕油罐建梯子,正好A点的正上方B点,问梯子最短需多少米?
(已知:油罐的底面半径是2m,高AB是5m,π取3)
A
B
A
B
A'
B'
A
变式精析
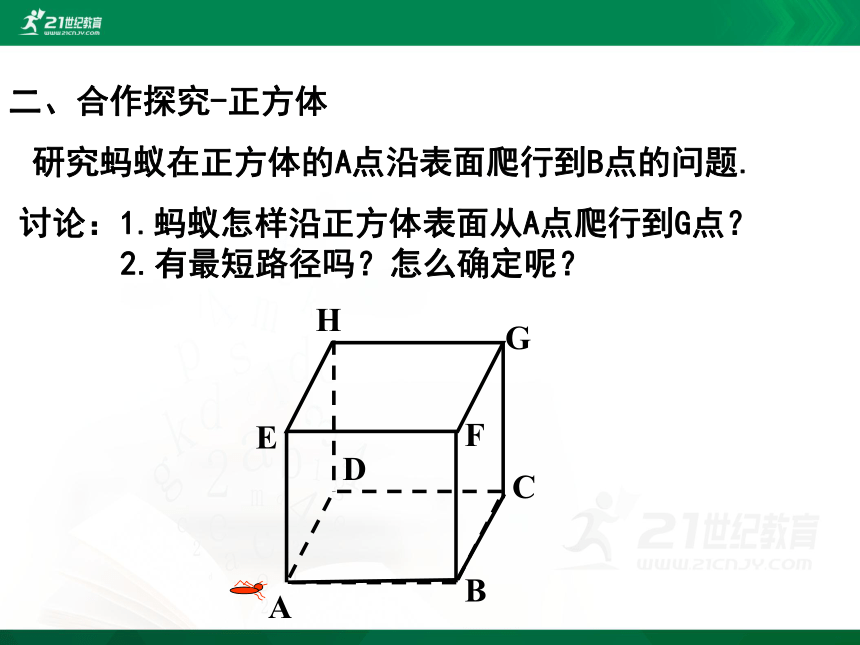
讨论:1.蚂蚁怎样沿正方体表面从A点爬行到G点?
2.有最短路径吗?怎么确定呢?
二、合作探究-正方体
研究蚂蚁在正方体的A点沿表面爬行到B点的问题.
A
B
C
D
E
F
G
H
正方体爬行路径
A
B
F
E
H
G
前(后)
上(下)
B
C
G
F
E
H
右(左)
上(下)
前(后)
右(左)
B
C
A
E
F
G
A
B
C
D
E
F
G
H
三种爬行路径的长度相同
正方体爬行路径
A
B
C
D
E
F
G
H
方法总结:
—侧面展开图中两点之间的连线段最短
B
C
A
E
F
G
变式精析
把正方体变成如左图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?那种爬行路径的距离最短?是多少?
A
B
F
G
E
H
2
4
1
前(后)
上(下)
(1)
A
D
H
G
E
F
2
4
1
左(右)
上(下)
(2)
A
B
C
F
G
E
4
2
1
前(后)
右
(左)
(3)
归纳总结:
四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。
如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离.
二、合作探究-台阶问题
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走.上午10:00,甲、乙两人相距多远?
三、典例精析
解:如图:已知A 是甲、乙的出发点,10:00甲到达B 点,乙到达C 点.则:
AB =2×6=12(千米),
AC =1×5=5(千米).
在Rt △ ABC 中,
∴BC =13(千米)
即甲乙两人相距13千米.
例2: 如图,笔直的公路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km.现在要在公路的AB段上建一个土特产品收购站E,使得C,D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
解:∵要使得C,D两村到E站的距离相等,
∴DE=CE.
∵DA⊥AB,CB⊥AB,
∴∠A=∠B=90°.
∴AE2+AD2=DE2,BE2+BC2=EC2.
∴AE2+AD2=BE2+BC2.
设AE=x km,则BE=AB-AE=(25-x)km.
∵DA=15 km,CB=10 km,
∴x2+152=(25-x)2+102.
解得x=10. ∴AE=10 km.
答:收购站E应建在离A点10 km处.
1.如图是一扇高为2 m,宽为1.5m的长方形门框,光头强有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板的最大的宽度为 ( )
A. 1.5 m B. 2 m
C. 2.5 m D. 3 m
C
四、课堂检测
2.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
四、课堂检测
解:将曲面沿AB展开,如图,
过点C作CE⊥AB于点E,连接CF.
在Rt△CEF中,∠CEF=90°,
EF=18-1-1=16(cm),
CE=12×60=30(cm),
由勾股定理,得
CF2= CE2+EF2=302+162=342.
∴ CF=34(cm).
答:蜘蛛所走的最短路线的长度是34 cm.
3. 如图,在一棵树的10 m高的B处有两只猴子. 一只猴子爬下树走到离树20 m的池塘的A处. 另一只爬到树顶D后直接跃到A处. 距离以直线计算.若两只猴子所经过的距离相等,则这棵树高多少米?
解:设树高为x m,则BD=x-10,由题意可知
BD+AD=BC+AC=10+20=30,
∴AD=30-BD=30-(x-10)=40-x.
在Rt△ACD中,
∴AD2=AC2+DC2,即(40-x)2=202+x2.
解得x=15.
答:这棵树高15 m.
四、课堂检测
4. 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是多少?
解:如图①,
AB2=AC2+BC2=32+(3+8)2=130.
如图②,
AB2=AC2+BC2=62+82=100.
因为130>100,所以AB=10.
答:它所行的最短路线的长是10.
四、课堂检测
5.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图,如图,他们在点A登陆后先往东走8 km到达点C,又往北走2 km,遇到障碍后又往西走3 km,再折向北走到6 km处往东一拐,仅走1 km就找到宝藏点B,问登陆点A到宝藏点B的直线距离是多少千米?
四、课堂检测
解:如图,过点B作BD⊥AC于点D,根据题意可知,
AD=8-3+1=6(km),
BD=2+6=8(km).
在Rt△ABD中,
AB2=AD2+BD2=62+82=100,
∴ AB=10(km).
答:登陆点A到宝藏点B的直线距离是10 km.
五、课堂小结
两点的距离最短问题
——转化成平面展开图中两点之间的连线段最短
本节课主要是应用勾股定理和它的逆定理来解决实际问题,在应用定理时,应注意:
1.没有图的要按题意画好图并标上字母;
2.不要用错定理.
六、布置作业
课本P14 习题1.4 第1,2,3,4题
谢谢聆听
第一章
勾股定理
1.3 勾股定理的应用
一、情景导入
B
A
蚂蚁怎么走最近
在一个圆柱石凳上,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,你们想一想,蚂蚁怎么走最近?
蚂蚁A→B的路线
B
A
A’
d
A
B
A’
A
B
B
A
O
B
A
路线一
路线二
路线三
路线四
研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题
讨论:1.蚂蚁怎样沿圆柱体侧面从A点爬行到B点?
2.有最短路径吗?怎么找到的?
B
A
我要从A点沿侧面爬行到B点,怎么爬呢?
二、合作探究活动-圆柱
A
B
A’
B
A
A’
r
O
h
侧面展开图
C
解:由题意得展开图,知AB即为最短路径,
AC=12, BC=
所以,最短路径是15cm
转化
B
A
在Rt △ ABC中,由勾股定理,得,
方法总结:
—侧面展开图中两点之间的连线段最短
A
B
A’
B
A
A’
r
O
h
例1:有一个圆柱形油罐,要以A点环绕油罐建梯子,正好A点的正上方B点,问梯子最短需多少米?
(已知:油罐的底面半径是2m,高AB是5m,π取3)
A
B
A
B
A'
B'
A
变式精析
讨论:1.蚂蚁怎样沿正方体表面从A点爬行到G点?
2.有最短路径吗?怎么确定呢?
二、合作探究-正方体
研究蚂蚁在正方体的A点沿表面爬行到B点的问题.
A
B
C
D
E
F
G
H
正方体爬行路径
A
B
F
E
H
G
前(后)
上(下)
B
C
G
F
E
H
右(左)
上(下)
前(后)
右(左)
B
C
A
E
F
G
A
B
C
D
E
F
G
H
三种爬行路径的长度相同
正方体爬行路径
A
B
C
D
E
F
G
H
方法总结:
—侧面展开图中两点之间的连线段最短
B
C
A
E
F
G
变式精析
把正方体变成如左图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?那种爬行路径的距离最短?是多少?
A
B
F
G
E
H
2
4
1
前(后)
上(下)
(1)
A
D
H
G
E
F
2
4
1
左(右)
上(下)
(2)
A
B
C
F
G
E
4
2
1
前(后)
右
(左)
(3)
归纳总结:
四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。
如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离.
二、合作探究-台阶问题
1.甲、乙两位探险者到沙漠进行探险,某日早晨8:00甲先出发,他以6km/h的速度向正东行走,1小时后乙出发,他以5km/h的速度向正北行走.上午10:00,甲、乙两人相距多远?
三、典例精析
解:如图:已知A 是甲、乙的出发点,10:00甲到达B 点,乙到达C 点.则:
AB =2×6=12(千米),
AC =1×5=5(千米).
在Rt △ ABC 中,
∴BC =13(千米)
即甲乙两人相距13千米.
例2: 如图,笔直的公路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km.现在要在公路的AB段上建一个土特产品收购站E,使得C,D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
解:∵要使得C,D两村到E站的距离相等,
∴DE=CE.
∵DA⊥AB,CB⊥AB,
∴∠A=∠B=90°.
∴AE2+AD2=DE2,BE2+BC2=EC2.
∴AE2+AD2=BE2+BC2.
设AE=x km,则BE=AB-AE=(25-x)km.
∵DA=15 km,CB=10 km,
∴x2+152=(25-x)2+102.
解得x=10. ∴AE=10 km.
答:收购站E应建在离A点10 km处.
1.如图是一扇高为2 m,宽为1.5m的长方形门框,光头强有一些薄木板要通过门框搬进屋内,在不能破坏门框,也不能锯短木板的情况下,能通过门框的木板的最大的宽度为 ( )
A. 1.5 m B. 2 m
C. 2.5 m D. 3 m
C
四、课堂检测
2.如图,圆柱形无盖玻璃容器,高18cm,底面周长为60cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.
四、课堂检测
解:将曲面沿AB展开,如图,
过点C作CE⊥AB于点E,连接CF.
在Rt△CEF中,∠CEF=90°,
EF=18-1-1=16(cm),
CE=12×60=30(cm),
由勾股定理,得
CF2= CE2+EF2=302+162=342.
∴ CF=34(cm).
答:蜘蛛所走的最短路线的长度是34 cm.
3. 如图,在一棵树的10 m高的B处有两只猴子. 一只猴子爬下树走到离树20 m的池塘的A处. 另一只爬到树顶D后直接跃到A处. 距离以直线计算.若两只猴子所经过的距离相等,则这棵树高多少米?
解:设树高为x m,则BD=x-10,由题意可知
BD+AD=BC+AC=10+20=30,
∴AD=30-BD=30-(x-10)=40-x.
在Rt△ACD中,
∴AD2=AC2+DC2,即(40-x)2=202+x2.
解得x=15.
答:这棵树高15 m.
四、课堂检测
4. 如图,一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是多少?
解:如图①,
AB2=AC2+BC2=32+(3+8)2=130.
如图②,
AB2=AC2+BC2=62+82=100.
因为130>100,所以AB=10.
答:它所行的最短路线的长是10.
四、课堂检测
5.假期中,王强和同学到某海岛上去探宝旅游,按照探宝图,如图,他们在点A登陆后先往东走8 km到达点C,又往北走2 km,遇到障碍后又往西走3 km,再折向北走到6 km处往东一拐,仅走1 km就找到宝藏点B,问登陆点A到宝藏点B的直线距离是多少千米?
四、课堂检测
解:如图,过点B作BD⊥AC于点D,根据题意可知,
AD=8-3+1=6(km),
BD=2+6=8(km).
在Rt△ABD中,
AB2=AD2+BD2=62+82=100,
∴ AB=10(km).
答:登陆点A到宝藏点B的直线距离是10 km.
五、课堂小结
两点的距离最短问题
——转化成平面展开图中两点之间的连线段最短
本节课主要是应用勾股定理和它的逆定理来解决实际问题,在应用定理时,应注意:
1.没有图的要按题意画好图并标上字母;
2.不要用错定理.
六、布置作业
课本P14 习题1.4 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
