高二数学人教A版 选修2-3 2.2.1条件概率 课件(共40张PPT)
文档属性
| 名称 | 高二数学人教A版 选修2-3 2.2.1条件概率 课件(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1015.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 00:00:00 | ||
图片预览











文档简介
一、探究:
三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
问题1:记最后一名同学抽到中奖奖券的事件为事件B,那么事件B发生的概率是多少?
问题2: 若已经知道第一名同学不中奖,那么最后一名同学中奖的概率又是多少?
解:记“最后一名同学中奖”为事件B, Ω 为所有结果组成的全体
探究:三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
用n(B)表示
事件B包含的基本
事件的个数
用W表示所有基本事件的集合,叫做基本事件空间(或样本空间)
知道第一名同学的结果会影响最后一名同学中奖的概率吗?
问题2:如果已经知道第一名同学没有中奖, 那么最后一名同学中奖的概率是多少?
在事件A发生的情况下,事件B发生等价于事件A和事件B同时发生,即事件AB发生,而事件AB中含有两个事件,即
事件A已经发生,只需在A的范围内考虑问题即可,我们记此时的事件空间为 ,则
A
W
另一方面,运用概率公式,我们容易得到
因此通过事件A和事件AB 的概率来表示:
由古典概型可知:
P(B)以试验下为条件,样本空间是
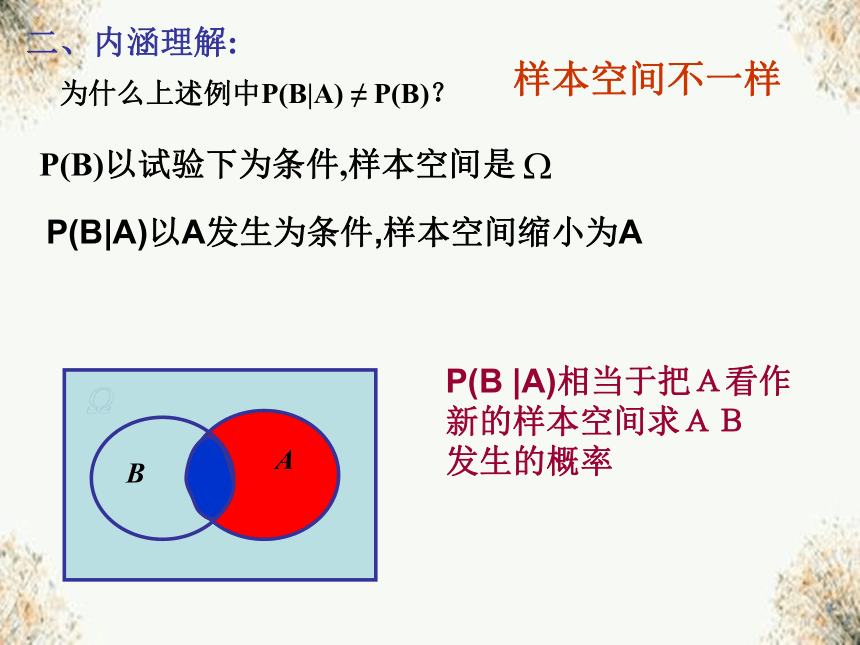
二、内涵理解:
A
B
P(B|A)以A发生为条件,样本空间缩小为A
P(B |A)相当于把A看作
新的样本空间求AB
发生的概率
样本空间不一样
为什么上述例中P(B|A) ≠ P(B)?
例1 某商店出售的100件商品的构成如下:
厂家 甲厂 乙厂 合计
一级品 50 43 93
二级品 3 4 7
合计 53 47 100
求:(1)任卖一件是甲厂生产的概率;
(2)某顾客买回一件该商品经检验是二级品,它是甲厂生产的概率.
条件概率
儒禁罚娇造瘴臻宝既委谦镑唾江躺吝号犹俺珊我办简绝嘲琶操研倘肛顺韧-条件概率-条件概率
例2 掷两颗骰子,
(1)其中有一颗为1点的概率;
(2)已知两颗骰子点数之和为7,
求其中有一颗为1点的概率.
掷骰子试验
杰甘颊醉缔硝干母谋赤屡戚贬棱潍士原删灼甲志路掀厕并皿防晰仓寇祷尝-条件概率-条件概率
分析:求P(B|A)的一般思想
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
设A,B为两个事件, 且P(A)>0, 称:
为在事件A发生的条件下,事件B发生的条件概率
P(B︱A)读作 :A发生的条件下B的概率
条件概率定义:
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例3、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题的概率。
解:法一:由(1)(2)可得,在第一次抽到理科题的条件下,第二次抽到理科题的概率为
解:法二:因为n(AB)= ,n(A)= ,所以
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题的概率。
6
12
反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
( 3 )利用条件概率公式求
课本练习题:
1.从1副不含大小王的52张扑克牌中不放回地抽取2次,每次抽1张,已知第1次抽到A,求第2次也抽到A的概率。
课本练习题:
2.100件产品中有5件次品,不放回地抽取2次,每次抽1次,已知第1次抽出的是次品,求第2次抽出正品的概率。
课本练习题:
2.100件产品中有5件次品,不放回地抽取2次,每次抽1次,已知第1次抽出的是次品,求第2次抽出正品的概率。
补充练习题:
3.一个盒子中有3个白球、2个黑球,每次从中不放回地任取1个球,连取两次,则在第一次取到黑球的条件下,第二次取到白球的概率是多少?
概率 P(B|A)与P(AB)的区别与联系
易错概念辨析
内涵再理解:
A
B
P(B |A)相当于把A看作
新的样本空间求AB
发生的概率
概率 P(B|A)与P(AB)的区别与联系
答案: C
练习2 一盒子装有4 只产品,其中有3 只一等品,1只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件A为“第一次取到的是一等品” ,事件B 为“第二次取到的是一等品”,试求条件概 P(B|A).
解
筑磕薛菠惜滋签陨珠为号锋酵纵栅靠啼倦砌捉贤生钢莱说桩救亲陷泵材崇-条件概率-条件概率
由条件概率的公式得
诉务铜谣翁疥胃砰察板狈旨甸昨榆浩矿徽险略均况踌性锤脊柯躺掏望爹懂-条件概率-条件概率
练习3:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(1)乙地为雨天时甲地也为雨天的概率是多少?
(2)甲地为雨天时乙地也为雨天的概率是多少?
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习3:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(3)甲乙两市至少一市下雨的概率是多少?
∵{甲乙两市至少一市下雨}=A∪B
而P(A∪B)=P(A)+P(B)-P(AB)
=20%+18%-12%
=26%
∴甲乙两市至少一市下雨的概率为26%
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习4. 某种动物由出生算起活20岁以上的概率为
0.8, 活到25岁以上的概率为0.4, 如果现在有一个
20岁的这种动物, 问它能活到25岁以上的概率是
多少?
设 A 表示“ 能活 20 岁以上 ” 的事件; B 表
示 “ 能活 25 岁以上”的事件,
则有
解
藤彪湛斥元氨视汗铬垄亮亥闪河页凌君惜飘充寒铃啼说结岭恕趁烬地吃唁-条件概率-条件概率
练习6. 将3封不同的信投入3个不同的信封,记事件A为“至少有1个信封为空”,事件B为“恰好有2个信封为空”,则P(B|A)等于多少?
练习7.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A=“三个人去的景点不相同”,B=“甲独自去一个景点”,则概率P(A|B)等于________.
条件概率的加法公式
(前提B、C是两个互斥事件)
例4 一张储蓄卡的密码共有6位数字,每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
解:设“第i次按对密码“为事件Ai(i=1,2),则
表示“不超过2次就按对密码”
(1)因为事件A1与事件 互斥,由概率的加法公式得
例4 一张储蓄卡的密码共有6位数字,每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
解:设“第i次按对密码“为事件Ai(i=1,2),则
表示“不超过2次就按对密码”
(2)设“最后一位按偶数”为事件B,则
辽宁高考真题
答案: B
2.(2011·湖南高考)如图,EFGH是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=______;(2)P(B|A)=______.
湖南高考真题
1. 条件概率的定义.
2. 条件概率的计算.
公式:
条件概率的加法公式
(前提B、C是两个互斥事件)
三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
问题1:记最后一名同学抽到中奖奖券的事件为事件B,那么事件B发生的概率是多少?
问题2: 若已经知道第一名同学不中奖,那么最后一名同学中奖的概率又是多少?
解:记“最后一名同学中奖”为事件B, Ω 为所有结果组成的全体
探究:三张奖券中只有一张能中奖,现分别由3名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两位小?
用n(B)表示
事件B包含的基本
事件的个数
用W表示所有基本事件的集合,叫做基本事件空间(或样本空间)
知道第一名同学的结果会影响最后一名同学中奖的概率吗?
问题2:如果已经知道第一名同学没有中奖, 那么最后一名同学中奖的概率是多少?
在事件A发生的情况下,事件B发生等价于事件A和事件B同时发生,即事件AB发生,而事件AB中含有两个事件,即
事件A已经发生,只需在A的范围内考虑问题即可,我们记此时的事件空间为 ,则
A
W
另一方面,运用概率公式,我们容易得到
因此通过事件A和事件AB 的概率来表示:
由古典概型可知:
P(B)以试验下为条件,样本空间是
二、内涵理解:
A
B
P(B|A)以A发生为条件,样本空间缩小为A
P(B |A)相当于把A看作
新的样本空间求AB
发生的概率
样本空间不一样
为什么上述例中P(B|A) ≠ P(B)?
例1 某商店出售的100件商品的构成如下:
厂家 甲厂 乙厂 合计
一级品 50 43 93
二级品 3 4 7
合计 53 47 100
求:(1)任卖一件是甲厂生产的概率;
(2)某顾客买回一件该商品经检验是二级品,它是甲厂生产的概率.
条件概率
儒禁罚娇造瘴臻宝既委谦镑唾江躺吝号犹俺珊我办简绝嘲琶操研倘肛顺韧-条件概率-条件概率
例2 掷两颗骰子,
(1)其中有一颗为1点的概率;
(2)已知两颗骰子点数之和为7,
求其中有一颗为1点的概率.
掷骰子试验
杰甘颊醉缔硝干母谋赤屡戚贬棱潍士原删灼甲志路掀厕并皿防晰仓寇祷尝-条件概率-条件概率
分析:求P(B|A)的一般思想
因为已经知道事件A必然发生,所以只需在A发生
的范围内考虑问题,即现在的样本空间为A。
因为在事件A发生的情况下事件B发生,等价于事
件A和事件B同时发生,即AB发生。
故其条件概率为
为了把条件概率推广到一般情形,不妨记原来的
样本空间为W,则有
设A,B为两个事件, 且P(A)>0, 称:
为在事件A发生的条件下,事件B发生的条件概率
P(B︱A)读作 :A发生的条件下B的概率
条件概率定义:
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道的事件数为
例3、在5道题中有3道理科题和2道文科题,如果不放回
地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题的概率。
解:法一:由(1)(2)可得,在第一次抽到理科题的条件下,第二次抽到理科题的概率为
解:法二:因为n(AB)= ,n(A)= ,所以
例3:在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:
(1)第一次抽取到理科题的概率;
(2)第一次和第二次都抽取到理科题的概率;
(3)在第一次抽到理科题的条件下,第二次抽到理科题的概率。
6
12
反思
求解条件概率的一般步骤:
(1)用字母表示有关事件
(2)求P(AB),P(A)或n(AB),n(A)
( 3 )利用条件概率公式求
课本练习题:
1.从1副不含大小王的52张扑克牌中不放回地抽取2次,每次抽1张,已知第1次抽到A,求第2次也抽到A的概率。
课本练习题:
2.100件产品中有5件次品,不放回地抽取2次,每次抽1次,已知第1次抽出的是次品,求第2次抽出正品的概率。
课本练习题:
2.100件产品中有5件次品,不放回地抽取2次,每次抽1次,已知第1次抽出的是次品,求第2次抽出正品的概率。
补充练习题:
3.一个盒子中有3个白球、2个黑球,每次从中不放回地任取1个球,连取两次,则在第一次取到黑球的条件下,第二次取到白球的概率是多少?
概率 P(B|A)与P(AB)的区别与联系
易错概念辨析
内涵再理解:
A
B
P(B |A)相当于把A看作
新的样本空间求AB
发生的概率
概率 P(B|A)与P(AB)的区别与联系
答案: C
练习2 一盒子装有4 只产品,其中有3 只一等品,1只二等品.从中取产品两次,每次任取一只,作不放回抽样.设事件A为“第一次取到的是一等品” ,事件B 为“第二次取到的是一等品”,试求条件概 P(B|A).
解
筑磕薛菠惜滋签陨珠为号锋酵纵栅靠啼倦砌捉贤生钢莱说桩救亲陷泵材崇-条件概率-条件概率
由条件概率的公式得
诉务铜谣翁疥胃砰察板狈旨甸昨榆浩矿徽险略均况踌性锤脊柯躺掏望爹懂-条件概率-条件概率
练习3:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(1)乙地为雨天时甲地也为雨天的概率是多少?
(2)甲地为雨天时乙地也为雨天的概率是多少?
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习3:甲乙两地都位于长江下游,根据一百多年的气象
记录,知道甲乙两地一年中雨天所占的比例分别为20%
和18%,两地同时下雨的比例为12%,问:
(3)甲乙两市至少一市下雨的概率是多少?
∵{甲乙两市至少一市下雨}=A∪B
而P(A∪B)=P(A)+P(B)-P(AB)
=20%+18%-12%
=26%
∴甲乙两市至少一市下雨的概率为26%
解:设A={甲地为雨天}, B={乙地为雨天},
则P(A)=20%,P(B)=18%,P(AB)=12%,
练习4. 某种动物由出生算起活20岁以上的概率为
0.8, 活到25岁以上的概率为0.4, 如果现在有一个
20岁的这种动物, 问它能活到25岁以上的概率是
多少?
设 A 表示“ 能活 20 岁以上 ” 的事件; B 表
示 “ 能活 25 岁以上”的事件,
则有
解
藤彪湛斥元氨视汗铬垄亮亥闪河页凌君惜飘充寒铃啼说结岭恕趁烬地吃唁-条件概率-条件概率
练习6. 将3封不同的信投入3个不同的信封,记事件A为“至少有1个信封为空”,事件B为“恰好有2个信封为空”,则P(B|A)等于多少?
练习7.甲、乙、丙三人到三个景点旅游,每人只去一个景点,设事件A=“三个人去的景点不相同”,B=“甲独自去一个景点”,则概率P(A|B)等于________.
条件概率的加法公式
(前提B、C是两个互斥事件)
例4 一张储蓄卡的密码共有6位数字,每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
解:设“第i次按对密码“为事件Ai(i=1,2),则
表示“不超过2次就按对密码”
(1)因为事件A1与事件 互斥,由概率的加法公式得
例4 一张储蓄卡的密码共有6位数字,每位数字都可从0—9中任选一个。某人在银行自动取款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过2次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率。
解:设“第i次按对密码“为事件Ai(i=1,2),则
表示“不超过2次就按对密码”
(2)设“最后一位按偶数”为事件B,则
辽宁高考真题
答案: B
2.(2011·湖南高考)如图,EFGH是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=______;(2)P(B|A)=______.
湖南高考真题
1. 条件概率的定义.
2. 条件概率的计算.
公式:
条件概率的加法公式
(前提B、C是两个互斥事件)
