高二数学人教A版 选修2-3 2.3.1离散型随机变量及其分布列2 课件(共23张PPT)
文档属性
| 名称 | 高二数学人教A版 选修2-3 2.3.1离散型随机变量及其分布列2 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-01 09:26:43 | ||
图片预览








文档简介
第二章 随机变量及其分布
2.1 离散型随机变量及其分布列(2)
复习
一、随机变量的定义:
二、随机变量的分类:
三、随机变量的分布列:
1、分布列的性质:
2、求分布列的步骤:
定值 求概率 列表
高考真题
2016天津高考16
某小组共10人,利用假期参加义工活动.已知参加义工活动次数为1,2,3的人数分别为3,3,4,.现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(II)设 X为选出的2人参加义工活动次数之差的绝对值,求随机变量 X的分布列
练习1:甲乙丙丁4人被随机分到ABC三个社区参加社会实践,要求每个社区至少有一人
(1)求甲乙两人都被分到A社区的概率
(2)求甲乙两人不在同一社区的概率
(3)设随机变量X为4人分到A社区的人数,求X的分布列
例1:
已知随机变量 的分布列如下:
-2
-1
3
2
1
0
分别求出随机变量⑴
;⑵
的分布列.
解:
且相应取值的概率没有变化
∴
的分布列为:
-1
1
0
⑴由
可得
的取值为 、
、0、
、1、
思考:若X是随机变量,Y=aX+b (ab为常数),Y是否为随机变量
例1:
已知随机变量 的分布列如下:
-2
-1
3
2
1
0
分别求出随机变量⑴
;⑵
的分布列.
解:
∴
的分布列为:
⑵由
可得
的取值为0、1、4、9
0
9
4
1
例2.在掷一枚图钉的随机试验中,令
如果针尖向上的概率为p,试写出随机变量X的分布列
解:根据分布列的性质,针尖向下的概率是(1-p),于是,随机变量X的分布列是:
X
0
1
P
1-p
p
像这样的分布列称为两点分布列.
*
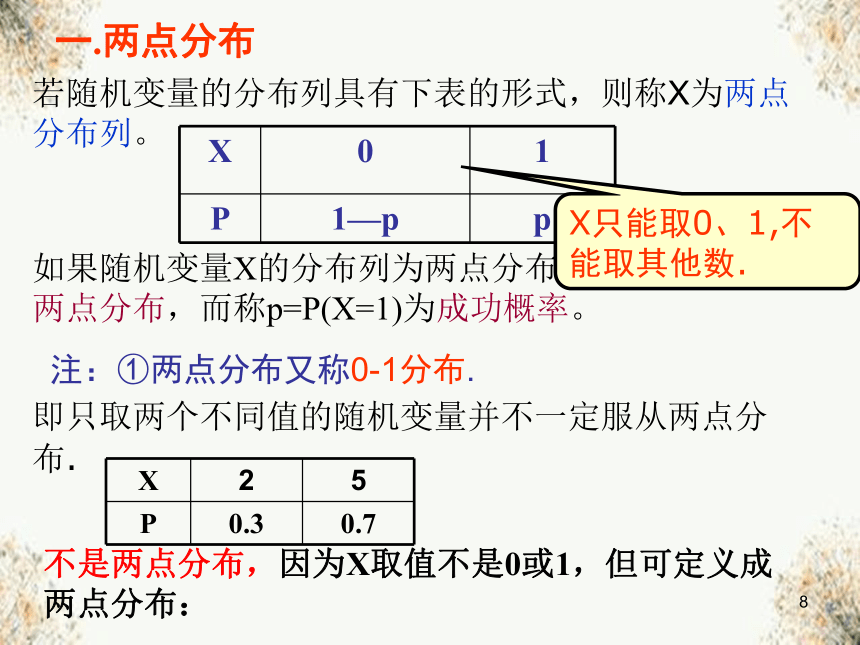
若随机变量的分布列具有下表的形式,则称X为两点分布列。
X
0
1
P
1—p
p
一.两点分布
如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。
注:①两点分布又称0-1分布.
X只能取0、1,不能取其他数.
X
2
5
P
0.3
0.7
即只取两个不同值的随机变量并不一定服从两点分布.
不是两点分布,因为X取值不是0或1,但可定义成两点分布:
*
X
2
5
P
0.3
0.7
但可定义:
Y=
0,X=2
1,X=5
此时Y服从两点分布.
③两点分布不仅可以用来研究只有两个结果的随机试验的概率分布规律,也可以用于研究某一随机事件是否发生的概率分布规律.如抽取的彩券是否中奖; 买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等等,都可以用两点分布列来研究
Y
0
1
P
0.3
0.7
②由于只有两个可能结果的随机试验叫伯努利试验,所以还称两点分布为伯努利分布.
*
课堂练习:
1-m
1、设某项试验成功的概率是失败的概率的2倍,用随机变量X描述1次试验的成功次数,则P(X=0)等于( )
A、0 B、1/2 C、1/3 D、2/3
2、对于0-1分布,设P(0)=m,0C
X
0
1
P
0.3
0.7
*
例3、在含有5件次品的100件产品中, 任取3件, 求取到的次品数X的分布列.
问:X的可能取哪些值?
变量X对应值的概率怎么求?
题中“任取3件”是指什么?
从所有的产品中依次不放回地任取三件产品
X取值为0,1,2,3
*
例3.在含有5件次品的100件产品中,任取3件,试求:(1)取到的次品数X的分布列; (2)至少取到1件次品的概率.
解(1)随机变量X的所有可能取值为0,1,2,3.
*
例3.在含有5件次品的100件产品中,任取3件,试求:(1)取到的次品数X的分布列; (2)至少取到1件次品的概率.
所以随机变量X的分布列是
X
0
1
2
3
P
(2)P(X≥1)=P(X=1)+P(X=2)+P(X=3)≈0.14400;
或P(X≥1)=1-P(X=0)=1- ≈0.14400;
如取小数,注意保留小数位不能太少,此外四舍五入时还要注意各个概率和等于1.
观察其分布列有何规律?能否将此规律推广到一般情形.
*
在含有 件次品的 件产品中, 任取 件, 求取到的次品数X的分布列.
M
N
n
(N≥M)
其中恰有X件次品数,则事件{X=k}发生的概率为
其中
,且
∴随机变量X的分布列是
X
0
1
…
m
P
…
m
m
这个分布列称为超几何分布列.
2.超几何分布.
*
说明:⑴ 超几何分布的模型是不放回抽样;
⑵ 超几何分布中的参数是M , N , n ;
(3) 注意成立条件为
如果随机变量X的分布列为超几何分布列,则称X服从超几何分布.
分布列
例如,如果共有10件产品中有6件次品,从中任取5件产品,则取出的产品中次品数X的取值范围是什么?
{1,2,3,4,5}
*
例4.在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和20个白球,这些球除颜色外完全相同.一次从中摸出5个球,至少摸到3个红球就中奖.求中奖的概率.
解:设摸出红球的个数为X,则X的所有可能值为0、1、2、3、4、5,且X服从超几何分布.
一次从中摸出5个球,摸到k(k=0,1,2,3,4,5)个红球的概率为
于是中奖的概率
P(X≥3)=P(X=3)+P(X=4)+P(X=5)
*
练习2 课本50页B组第1题 :老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格,某同学只能背诵其中的6篇,求:
(1)抽到他能背诵的课文的数量的分布列
(2)他能及格的概率
练习3:盒中装有12个零件,其中9个正品,3个次品,从中任取1个,若取到次品不再放回,接着再取1个零件,直到取到正品为止,求取到的次品数X的分布列
X服从超几何分布吗?
练习4:盒中装有大小相同的12个乒乓球,其中9个新的,3个旧的(用过的求即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数Y是一个随机变量,求Y的分布列
练习5.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
小结:
1.两点分布又称0-1分布,两点分布中只有两个结果,且两个结果对立
2.超几何分布
超几何分布模型由比较明显的两部分构成
一般是不放回抽样
2.1 离散型随机变量及其分布列(2)
复习
一、随机变量的定义:
二、随机变量的分类:
三、随机变量的分布列:
1、分布列的性质:
2、求分布列的步骤:
定值 求概率 列表
高考真题
2016天津高考16
某小组共10人,利用假期参加义工活动.已知参加义工活动次数为1,2,3的人数分别为3,3,4,.现从这10人中随机选出2人作为该组代表参加座谈会.
(I)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(II)设 X为选出的2人参加义工活动次数之差的绝对值,求随机变量 X的分布列
练习1:甲乙丙丁4人被随机分到ABC三个社区参加社会实践,要求每个社区至少有一人
(1)求甲乙两人都被分到A社区的概率
(2)求甲乙两人不在同一社区的概率
(3)设随机变量X为4人分到A社区的人数,求X的分布列
例1:
已知随机变量 的分布列如下:
-2
-1
3
2
1
0
分别求出随机变量⑴
;⑵
的分布列.
解:
且相应取值的概率没有变化
∴
的分布列为:
-1
1
0
⑴由
可得
的取值为 、
、0、
、1、
思考:若X是随机变量,Y=aX+b (ab为常数),Y是否为随机变量
例1:
已知随机变量 的分布列如下:
-2
-1
3
2
1
0
分别求出随机变量⑴
;⑵
的分布列.
解:
∴
的分布列为:
⑵由
可得
的取值为0、1、4、9
0
9
4
1
例2.在掷一枚图钉的随机试验中,令
如果针尖向上的概率为p,试写出随机变量X的分布列
解:根据分布列的性质,针尖向下的概率是(1-p),于是,随机变量X的分布列是:
X
0
1
P
1-p
p
像这样的分布列称为两点分布列.
*
若随机变量的分布列具有下表的形式,则称X为两点分布列。
X
0
1
P
1—p
p
一.两点分布
如果随机变量X的分布列为两点分布列,就称X服从两点分布,而称p=P(X=1)为成功概率。
注:①两点分布又称0-1分布.
X只能取0、1,不能取其他数.
X
2
5
P
0.3
0.7
即只取两个不同值的随机变量并不一定服从两点分布.
不是两点分布,因为X取值不是0或1,但可定义成两点分布:
*
X
2
5
P
0.3
0.7
但可定义:
Y=
0,X=2
1,X=5
此时Y服从两点分布.
③两点分布不仅可以用来研究只有两个结果的随机试验的概率分布规律,也可以用于研究某一随机事件是否发生的概率分布规律.如抽取的彩券是否中奖; 买回的一件产品是否为正品;新生婴儿的性别;投篮是否命中等等,都可以用两点分布列来研究
Y
0
1
P
0.3
0.7
②由于只有两个可能结果的随机试验叫伯努利试验,所以还称两点分布为伯努利分布.
*
课堂练习:
1-m
1、设某项试验成功的概率是失败的概率的2倍,用随机变量X描述1次试验的成功次数,则P(X=0)等于( )
A、0 B、1/2 C、1/3 D、2/3
2、对于0-1分布,设P(0)=m,0
X
0
1
P
0.3
0.7
*
例3、在含有5件次品的100件产品中, 任取3件, 求取到的次品数X的分布列.
问:X的可能取哪些值?
变量X对应值的概率怎么求?
题中“任取3件”是指什么?
从所有的产品中依次不放回地任取三件产品
X取值为0,1,2,3
*
例3.在含有5件次品的100件产品中,任取3件,试求:(1)取到的次品数X的分布列; (2)至少取到1件次品的概率.
解(1)随机变量X的所有可能取值为0,1,2,3.
*
例3.在含有5件次品的100件产品中,任取3件,试求:(1)取到的次品数X的分布列; (2)至少取到1件次品的概率.
所以随机变量X的分布列是
X
0
1
2
3
P
(2)P(X≥1)=P(X=1)+P(X=2)+P(X=3)≈0.14400;
或P(X≥1)=1-P(X=0)=1- ≈0.14400;
如取小数,注意保留小数位不能太少,此外四舍五入时还要注意各个概率和等于1.
观察其分布列有何规律?能否将此规律推广到一般情形.
*
在含有 件次品的 件产品中, 任取 件, 求取到的次品数X的分布列.
M
N
n
(N≥M)
其中恰有X件次品数,则事件{X=k}发生的概率为
其中
,且
∴随机变量X的分布列是
X
0
1
…
m
P
…
m
m
这个分布列称为超几何分布列.
2.超几何分布.
*
说明:⑴ 超几何分布的模型是不放回抽样;
⑵ 超几何分布中的参数是M , N , n ;
(3) 注意成立条件为
如果随机变量X的分布列为超几何分布列,则称X服从超几何分布.
分布列
例如,如果共有10件产品中有6件次品,从中任取5件产品,则取出的产品中次品数X的取值范围是什么?
{1,2,3,4,5}
*
例4.在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和20个白球,这些球除颜色外完全相同.一次从中摸出5个球,至少摸到3个红球就中奖.求中奖的概率.
解:设摸出红球的个数为X,则X的所有可能值为0、1、2、3、4、5,且X服从超几何分布.
一次从中摸出5个球,摸到k(k=0,1,2,3,4,5)个红球的概率为
于是中奖的概率
P(X≥3)=P(X=3)+P(X=4)+P(X=5)
*
练习2 课本50页B组第1题 :老师要从10篇课文中随机抽3篇让学生背诵,规定至少要背出其中2篇才能及格,某同学只能背诵其中的6篇,求:
(1)抽到他能背诵的课文的数量的分布列
(2)他能及格的概率
练习3:盒中装有12个零件,其中9个正品,3个次品,从中任取1个,若取到次品不再放回,接着再取1个零件,直到取到正品为止,求取到的次品数X的分布列
X服从超几何分布吗?
练习4:盒中装有大小相同的12个乒乓球,其中9个新的,3个旧的(用过的求即为旧的),从盒中任取3个使用,用完后装回盒中,此时盒中旧球个数Y是一个随机变量,求Y的分布列
练习5.已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
小结:
1.两点分布又称0-1分布,两点分布中只有两个结果,且两个结果对立
2.超几何分布
超几何分布模型由比较明显的两部分构成
一般是不放回抽样
