新版华东师大版八年级数学上册第12章整式的乘除检测题(word版,含答案)
文档属性
| 名称 | 新版华东师大版八年级数学上册第12章整式的乘除检测题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 170.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 00:00:00 | ||
图片预览


文档简介
第12章检测题
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.(2019·南通)下列计算,正确的是(
)
A.a2·a3=a6
B.2a2-a=a
C.a6÷a2=a3
D.(a2)3=a6
2.(2019·贵阳)选择计算(-4xy2+3x2y)(4xy2+3x2y)的最佳方法是(
)
A.运用多项式乘多项式法则
B.运用平方差公式
C.运用单项式乘多项式法则
D.运用完全平方公式
3.(2019·无锡)分解因式4x2-y2的结果是(
)
A.(4x+y)(4x-y)
B.4(x+y)(x-y)
C.(2x+y)(2x-y)
D.2(x+y)(x-y)
4.若(x-2y)2=(x+2y)2+m,则m等于(
)
A.4xy
B.-4xy
C.8xy
D.-8xy
5.已知3a=5,9b=10,则3a+2b等于(
)
A.50
B.-5
C.15
D.27a+b
6.(2019·河北)小明总结了以下结论:①a(b+c)=ab+ac;②a(b-c)=ab-ac;③(b-c)÷a=b÷a-c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0).其中一定成立的个数是(
)
A.1
B.2
C.3
D.4
7.(2019·荆门)下列运算不正确的是(
)
A.xy+x-y-1=(x-1)(y+1)
B.x2+y2+z2+xy+yz+zx=(x+y+z)2
C.(x+y)(x2-xy+y2)=x3+y3
D.(x-y)3=x3-3x2y+3xy2-y3
8.(2019·柳州)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是(
)
A.-6
B.6
C.5
D.-5
9.(2019·烟台)南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”.
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
则(a+b)9展开式中所有项的系数和是(
)
A.128
B.256
C.512
D.1024
10.(宁波中考)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为(
)
A.2a
B.2b
C.2a-2b
D.-2b
二、填空题(每小题3分,共15分)
11.多项式ax2-a与多项式x2-2x+1的公因式是____.
12.(2019·徐州)若a=b+2,则代数式a2-2ab+b2的值为____.
13.已知2x=4y+1,27y=3x-1,则x-y=____.
14.(2019·大庆)分解因式:a2b+ab2-a-b=_______.
15.(2019·遂宁)阅读材料:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:(4+i)+(6-2i)=(4+6)+(1-2)i=10-i;
(2-i)(3+i)=6-3i+2i-i2=6-i-(-1)=7-i;
(4+i)(4-i)=16-i2=16-(-1)=17;
(2+i)2=4+4i+i2=4+4i-1=3+4i.
根据以上信息,完成下面计算:
(1+2i)(2-i)+(2-i)2=________.
三、解答题(共75分)
16.(8分)计算:
(1)(2019·武汉)(2x2)3-x2·x4;
(2)[3a2+2b(3a-2b)+b(4b-4a)]÷2a.
17.(9分)用简便方法计算:
(1)99×101×10
001+1;
(2)932+232-93×46.
18.(9分)分解因式:
(1)(2019·河池)(x-1)2+2(x-5);
(2)6xy2-9x2y-y3.
19.(9分)(2019·凉山州)先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-.
20.(9分)(大庆中考)已知:x2-y2=12,x+y=3,求2x2-2xy的值.
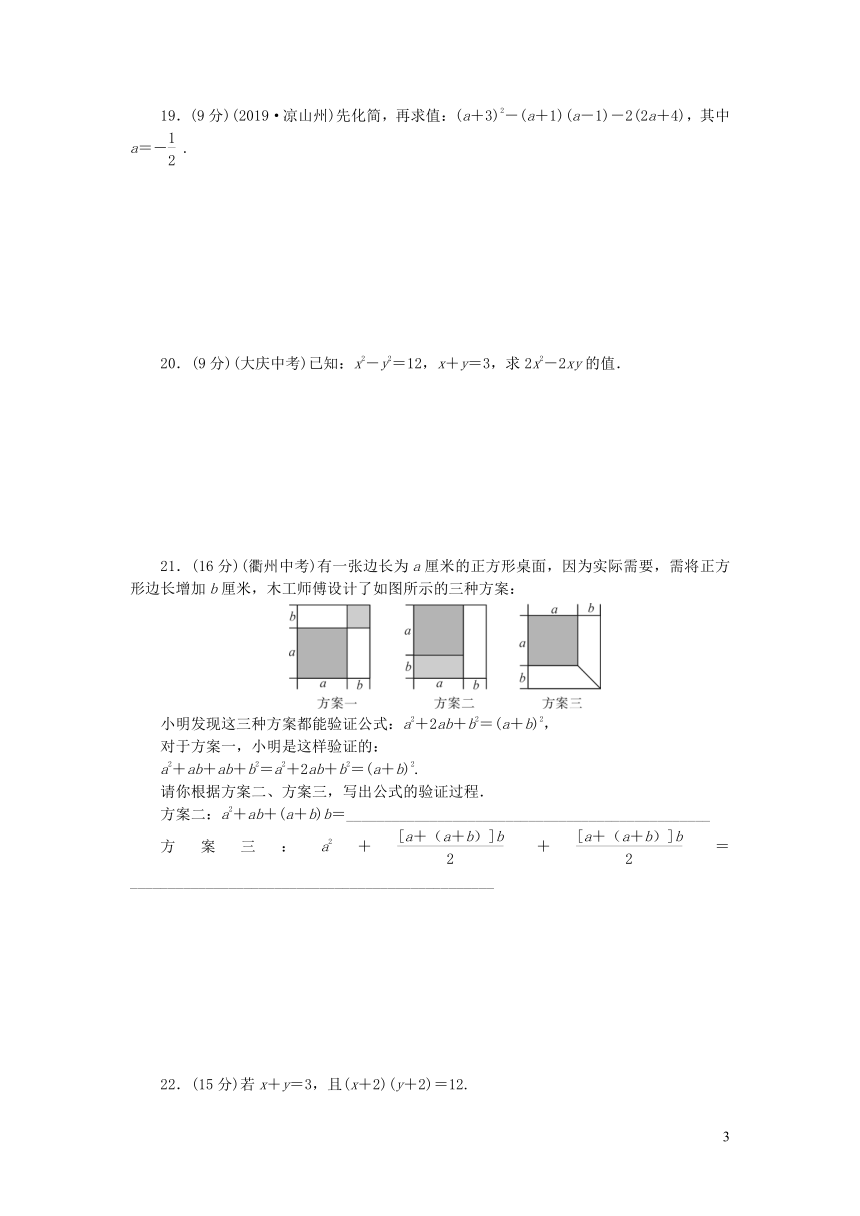
21.(16分)(衢州中考)有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=________________________________________________
方案三:a2++=________________________________________________
22.(15分)若x+y=3,且(x+2)(y+2)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
第12章检测题(答案版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.(2019·南通)下列计算,正确的是(
D
)
A.a2·a3=a6
B.2a2-a=a
C.a6÷a2=a3
D.(a2)3=a6
2.(2019·贵阳)选择计算(-4xy2+3x2y)(4xy2+3x2y)的最佳方法是(
B
)
A.运用多项式乘多项式法则
B.运用平方差公式
C.运用单项式乘多项式法则
D.运用完全平方公式
3.(2019·无锡)分解因式4x2-y2的结果是(
C
)
A.(4x+y)(4x-y)
B.4(x+y)(x-y)
C.(2x+y)(2x-y)
D.2(x+y)(x-y)
4.若(x-2y)2=(x+2y)2+m,则m等于(
D
)
A.4xy
B.-4xy
C.8xy
D.-8xy
5.已知3a=5,9b=10,则3a+2b等于(
A
)
A.50
B.-5
C.15
D.27a+b
6.(2019·河北)小明总结了以下结论:①a(b+c)=ab+ac;②a(b-c)=ab-ac;③(b-c)÷a=b÷a-c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0).其中一定成立的个数是(
C
)
A.1
B.2
C.3
D.4
7.(2019·荆门)下列运算不正确的是(
B
)
A.xy+x-y-1=(x-1)(y+1)
B.x2+y2+z2+xy+yz+zx=(x+y+z)2
C.(x+y)(x2-xy+y2)=x3+y3
D.(x-y)3=x3-3x2y+3xy2-y3
8.(2019·柳州)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是(
C
)
A.-6
B.6
C.5
D.-5
9.(2019·烟台)南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”.
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
则(a+b)9展开式中所有项的系数和是(
C
)
A.128
B.256
C.512
D.1024
10.(宁波中考)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为(
B
)
A.2a
B.2b
C.2a-2b
D.-2b
二、填空题(每小题3分,共15分)
11.多项式ax2-a与多项式x2-2x+1的公因式是x-1.
12.(2019·徐州)若a=b+2,则代数式a2-2ab+b2的值为__4__.
13.已知2x=4y+1,27y=3x-1,则x-y=3.
14.(2019·大庆)分解因式:a2b+ab2-a-b=__(ab-1)(a+b)__.
15.(2019·遂宁)阅读材料:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:(4+i)+(6-2i)=(4+6)+(1-2)i=10-i;
(2-i)(3+i)=6-3i+2i-i2=6-i-(-1)=7-i;
(4+i)(4-i)=16-i2=16-(-1)=17;
(2+i)2=4+4i+i2=4+4i-1=3+4i.
根据以上信息,完成下面计算:
(1+2i)(2-i)+(2-i)2=__7-i__.
三、解答题(共75分)
16.(8分)计算:
(1)(2019·武汉)(2x2)3-x2·x4;
(2)[3a2+2b(3a-2b)+b(4b-4a)]÷2a.
解:(1)原式=7x6
(2)原式=a+b
17.(9分)用简便方法计算:
(1)99×101×10
001+1;
(2)932+232-93×46.
解:(1)原式=108
(2)原式=4900
18.(9分)分解因式:
(1)(2019·河池)(x-1)2+2(x-5);
(2)6xy2-9x2y-y3.
解:(1)原式=(x+3)(x-3)
(2)原式=-y(3x-y)2
19.(9分)(2019·凉山州)先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-.
解:原式=a2+6a+9-(a2-1)-4a-8=2a+2,将a=-代入原式=2×(-)+2=1
20.(9分)(大庆中考)已知:x2-y2=12,x+y=3,求2x2-2xy的值.
解:∵x2-y2=12,∴(x+y)(x-y)=12,∵x+y=3①,∴x-y=4②,①+②,得2x=7,∴2x2-2xy=2x(x-y)=7×4=28
21.(16分)(衢州中考)有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2
方案三:a2++=a2+ab+b2+ab+b2=a2+2ab+b2=(a+b)2
22.(15分)若x+y=3,且(x+2)(y+2)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
解:(1)由(x+2)(y+2)=12得xy+2(x+y)+4=12,∵x+y=3,∴xy=2 (2)x2+3xy+y2=(x+y)2+xy,又∵x+y=3,xy=2,∴原式=32+2=11
5
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.(2019·南通)下列计算,正确的是(
)
A.a2·a3=a6
B.2a2-a=a
C.a6÷a2=a3
D.(a2)3=a6
2.(2019·贵阳)选择计算(-4xy2+3x2y)(4xy2+3x2y)的最佳方法是(
)
A.运用多项式乘多项式法则
B.运用平方差公式
C.运用单项式乘多项式法则
D.运用完全平方公式
3.(2019·无锡)分解因式4x2-y2的结果是(
)
A.(4x+y)(4x-y)
B.4(x+y)(x-y)
C.(2x+y)(2x-y)
D.2(x+y)(x-y)
4.若(x-2y)2=(x+2y)2+m,则m等于(
)
A.4xy
B.-4xy
C.8xy
D.-8xy
5.已知3a=5,9b=10,则3a+2b等于(
)
A.50
B.-5
C.15
D.27a+b
6.(2019·河北)小明总结了以下结论:①a(b+c)=ab+ac;②a(b-c)=ab-ac;③(b-c)÷a=b÷a-c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0).其中一定成立的个数是(
)
A.1
B.2
C.3
D.4
7.(2019·荆门)下列运算不正确的是(
)
A.xy+x-y-1=(x-1)(y+1)
B.x2+y2+z2+xy+yz+zx=(x+y+z)2
C.(x+y)(x2-xy+y2)=x3+y3
D.(x-y)3=x3-3x2y+3xy2-y3
8.(2019·柳州)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是(
)
A.-6
B.6
C.5
D.-5
9.(2019·烟台)南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”.
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
则(a+b)9展开式中所有项的系数和是(
)
A.128
B.256
C.512
D.1024
10.(宁波中考)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为(
)
A.2a
B.2b
C.2a-2b
D.-2b
二、填空题(每小题3分,共15分)
11.多项式ax2-a与多项式x2-2x+1的公因式是____.
12.(2019·徐州)若a=b+2,则代数式a2-2ab+b2的值为____.
13.已知2x=4y+1,27y=3x-1,则x-y=____.
14.(2019·大庆)分解因式:a2b+ab2-a-b=_______.
15.(2019·遂宁)阅读材料:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:(4+i)+(6-2i)=(4+6)+(1-2)i=10-i;
(2-i)(3+i)=6-3i+2i-i2=6-i-(-1)=7-i;
(4+i)(4-i)=16-i2=16-(-1)=17;
(2+i)2=4+4i+i2=4+4i-1=3+4i.
根据以上信息,完成下面计算:
(1+2i)(2-i)+(2-i)2=________.
三、解答题(共75分)
16.(8分)计算:
(1)(2019·武汉)(2x2)3-x2·x4;
(2)[3a2+2b(3a-2b)+b(4b-4a)]÷2a.
17.(9分)用简便方法计算:
(1)99×101×10
001+1;
(2)932+232-93×46.
18.(9分)分解因式:
(1)(2019·河池)(x-1)2+2(x-5);
(2)6xy2-9x2y-y3.
19.(9分)(2019·凉山州)先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-.
20.(9分)(大庆中考)已知:x2-y2=12,x+y=3,求2x2-2xy的值.
21.(16分)(衢州中考)有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=________________________________________________
方案三:a2++=________________________________________________
22.(15分)若x+y=3,且(x+2)(y+2)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
第12章检测题(答案版)
(时间:100分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.(2019·南通)下列计算,正确的是(
D
)
A.a2·a3=a6
B.2a2-a=a
C.a6÷a2=a3
D.(a2)3=a6
2.(2019·贵阳)选择计算(-4xy2+3x2y)(4xy2+3x2y)的最佳方法是(
B
)
A.运用多项式乘多项式法则
B.运用平方差公式
C.运用单项式乘多项式法则
D.运用完全平方公式
3.(2019·无锡)分解因式4x2-y2的结果是(
C
)
A.(4x+y)(4x-y)
B.4(x+y)(x-y)
C.(2x+y)(2x-y)
D.2(x+y)(x-y)
4.若(x-2y)2=(x+2y)2+m,则m等于(
D
)
A.4xy
B.-4xy
C.8xy
D.-8xy
5.已知3a=5,9b=10,则3a+2b等于(
A
)
A.50
B.-5
C.15
D.27a+b
6.(2019·河北)小明总结了以下结论:①a(b+c)=ab+ac;②a(b-c)=ab-ac;③(b-c)÷a=b÷a-c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0).其中一定成立的个数是(
C
)
A.1
B.2
C.3
D.4
7.(2019·荆门)下列运算不正确的是(
B
)
A.xy+x-y-1=(x-1)(y+1)
B.x2+y2+z2+xy+yz+zx=(x+y+z)2
C.(x+y)(x2-xy+y2)=x3+y3
D.(x-y)3=x3-3x2y+3xy2-y3
8.(2019·柳州)定义:形如a+bi的数称为复数(其中a和b为实数,i为虚数单位,规定i2=-1),a称为复数的实部,b称为复数的虚部.复数可以进行四则运算,运算的结果还是一个复数.例如(1+3i)2=12+2×1×3i+(3i)2=1+6i+9i2=1+6i-9=-8+6i,因此,(1+3i)2的实部是-8,虚部是6.已知复数(3-mi)2的虚部是12,则实部是(
C
)
A.-6
B.6
C.5
D.-5
9.(2019·烟台)南宋数学家杨辉在其著作《详解九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”.
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
……
则(a+b)9展开式中所有项的系数和是(
C
)
A.128
B.256
C.512
D.1024
10.(宁波中考)在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图①,图②两种方式放置(图①,图②中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图①中阴影部分的面积为S1,图②中阴影部分的面积为S2.当AD-AB=2时,S2-S1的值为(
B
)
A.2a
B.2b
C.2a-2b
D.-2b
二、填空题(每小题3分,共15分)
11.多项式ax2-a与多项式x2-2x+1的公因式是x-1.
12.(2019·徐州)若a=b+2,则代数式a2-2ab+b2的值为__4__.
13.已知2x=4y+1,27y=3x-1,则x-y=3.
14.(2019·大庆)分解因式:a2b+ab2-a-b=__(ab-1)(a+b)__.
15.(2019·遂宁)阅读材料:定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算:(4+i)+(6-2i)=(4+6)+(1-2)i=10-i;
(2-i)(3+i)=6-3i+2i-i2=6-i-(-1)=7-i;
(4+i)(4-i)=16-i2=16-(-1)=17;
(2+i)2=4+4i+i2=4+4i-1=3+4i.
根据以上信息,完成下面计算:
(1+2i)(2-i)+(2-i)2=__7-i__.
三、解答题(共75分)
16.(8分)计算:
(1)(2019·武汉)(2x2)3-x2·x4;
(2)[3a2+2b(3a-2b)+b(4b-4a)]÷2a.
解:(1)原式=7x6
(2)原式=a+b
17.(9分)用简便方法计算:
(1)99×101×10
001+1;
(2)932+232-93×46.
解:(1)原式=108
(2)原式=4900
18.(9分)分解因式:
(1)(2019·河池)(x-1)2+2(x-5);
(2)6xy2-9x2y-y3.
解:(1)原式=(x+3)(x-3)
(2)原式=-y(3x-y)2
19.(9分)(2019·凉山州)先化简,再求值:(a+3)2-(a+1)(a-1)-2(2a+4),其中a=-.
解:原式=a2+6a+9-(a2-1)-4a-8=2a+2,将a=-代入原式=2×(-)+2=1
20.(9分)(大庆中考)已知:x2-y2=12,x+y=3,求2x2-2xy的值.
解:∵x2-y2=12,∴(x+y)(x-y)=12,∵x+y=3①,∴x-y=4②,①+②,得2x=7,∴2x2-2xy=2x(x-y)=7×4=28
21.(16分)(衢州中考)有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:
小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,
对于方案一,小明是这样验证的:
a2+ab+ab+b2=a2+2ab+b2=(a+b)2.
请你根据方案二、方案三,写出公式的验证过程.
方案二:a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2
方案三:a2++=a2+ab+b2+ab+b2=a2+2ab+b2=(a+b)2
22.(15分)若x+y=3,且(x+2)(y+2)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
解:(1)由(x+2)(y+2)=12得xy+2(x+y)+4=12,∵x+y=3,∴xy=2 (2)x2+3xy+y2=(x+y)2+xy,又∵x+y=3,xy=2,∴原式=32+2=11
5
