1.1.2 探究勾股定理课件(共27张PPT)
文档属性
| 名称 | 1.1.2 探究勾股定理课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 00:00:00 | ||
图片预览



文档简介
2020年秋季北师大版八年级上册
第一章
勾股定理
1.1 探究勾股定理(二)
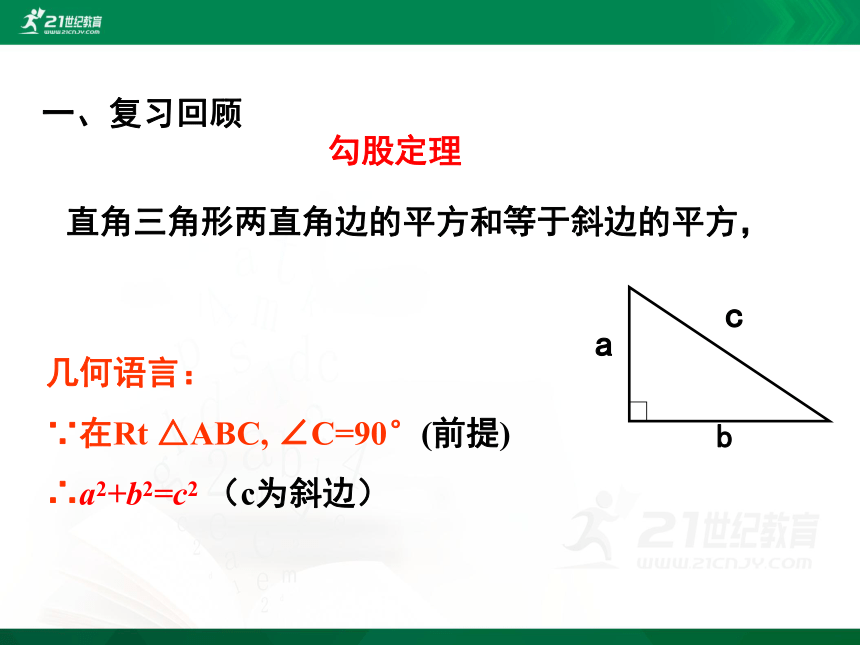
一、复习回顾
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
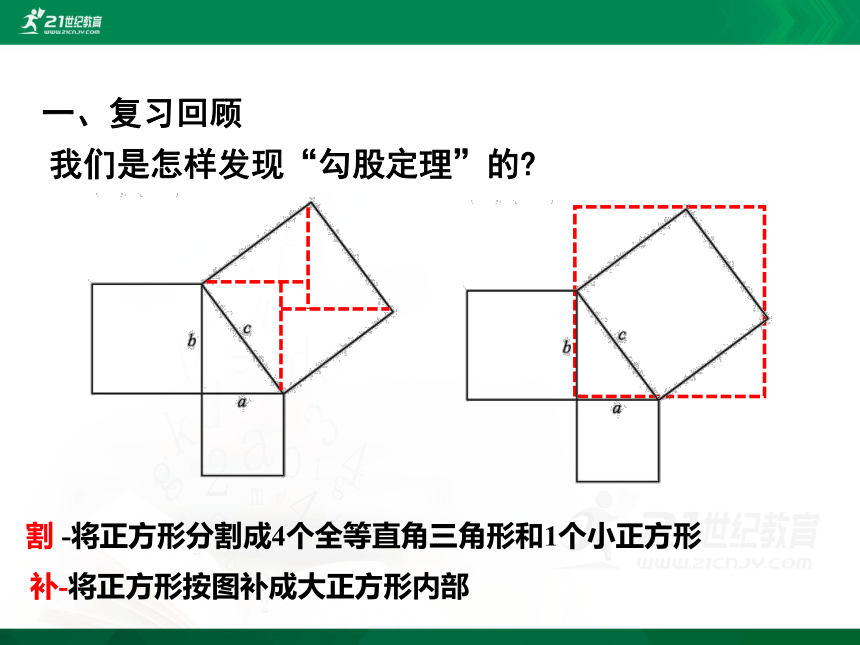
一、复习回顾
我们是怎样发现“勾股定理”的?
割 -将正方形分割成4个全等直角三角形和1个小正方形
补-将正方形按图补成大正方形内部
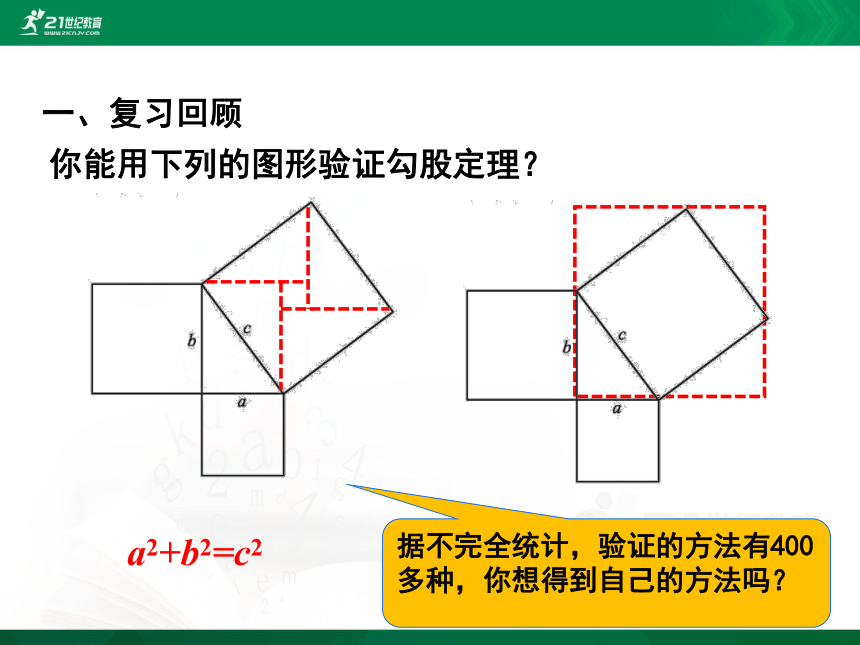
一、复习回顾
你能用下列的图形验证勾股定理?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
a2+b2=c2
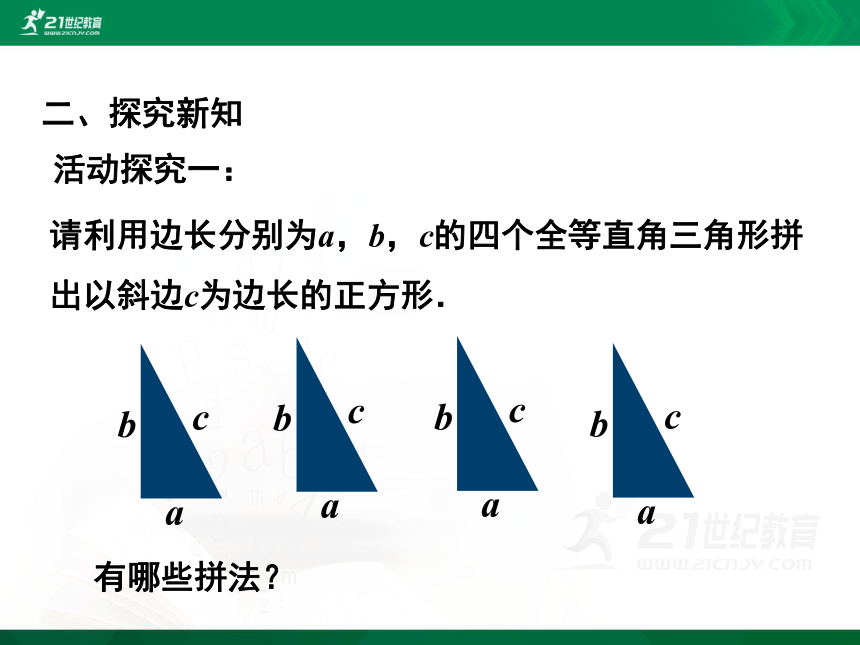
二、探究新知
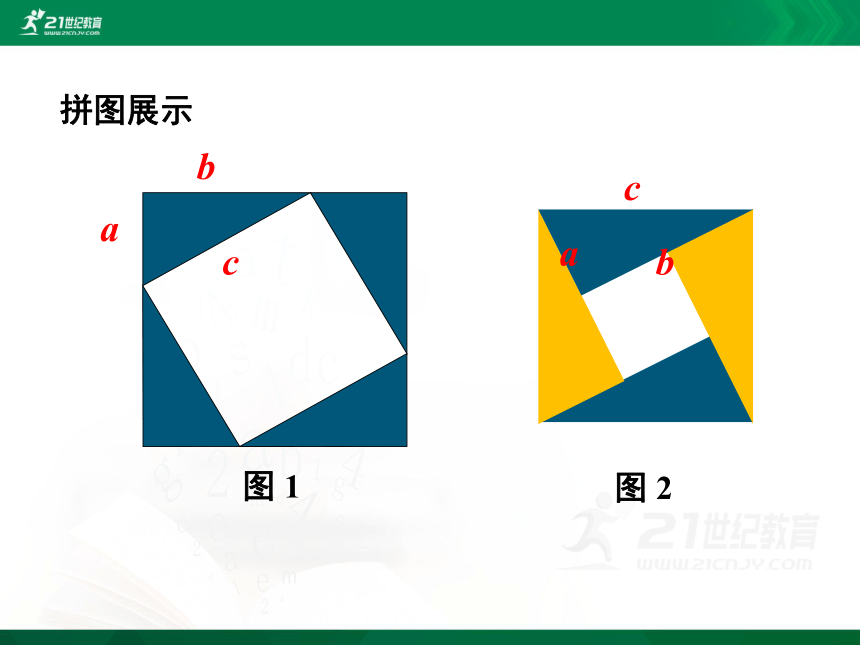
请利用边长分别为a,b,c的四个全等直角三角形拼出以斜边c为边长的正方形.
活动探究一:
有哪些拼法?
a
b
c
a
b
c
a
b
c
a
b
c
拼图展示
图 1
图 2
a
b
c
a
b
c
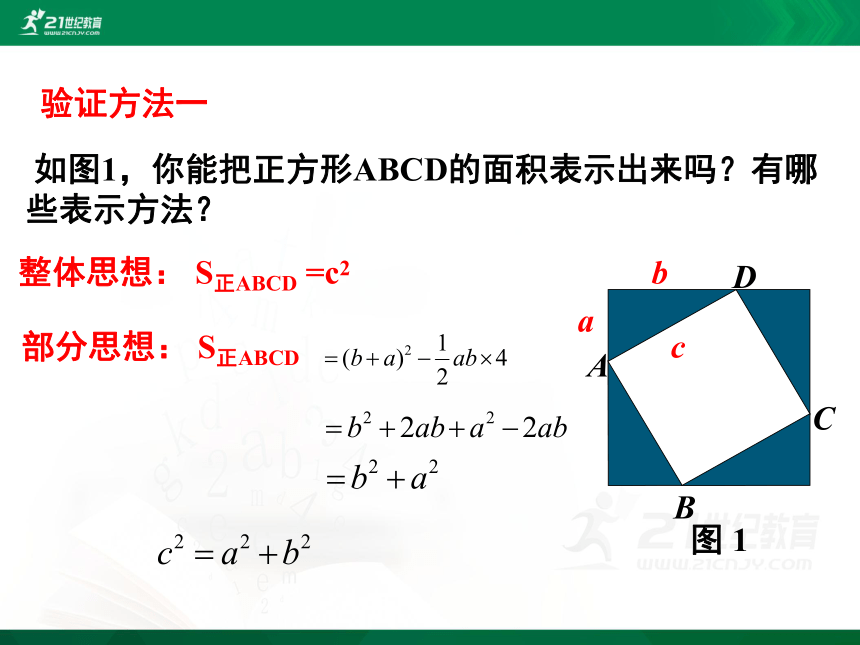
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
图 1
a
b
c
A
B
C
D
整体思想: S正ABCD =c2
部分思想: S正ABCD
验证方法一
图 2
a
b
c
验证方法二
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
整体思想:S正ABCD =c2
部分思想:S正ABCD
“勾股定理”的验证方法:
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
二、探究新知
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2 。
延伸拓展
A
B
C
A的面积
SA
B的面积
SB
C的面积
SC
图1
图2
A
B
C
图1
图2
8
9
29
5
8
9
钝角三角形:a2+b2 < c2
锐角三角形:a2+b2 > c2
例1 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
三、典例精析
解:在Rt△ABC中,根据勾股定理,
∴BC?=AB?-AC?
=500?-400?
=3002
∴BC=300 m
V敌方汽车=S÷t=300÷10=30 (m/s)
答:敌方汽车的速度为30 m/s
例2 如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
三、典例精析
解:设这棵树折断后有x米高,则折断的部分为(18-x)米,根据勾股定理,得
∴x?+6?=(18-x)?
∴解得x=8 m
答:这棵树折断后有8米高
例3.如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
“总统证明法”
三、典例精析
S等腰直角三角形
S等腰直角三角形
1. 一艘船由于风向的原因先向正东方向航行了160 km,然后向正北方向航行了120 km,这时它离出发点有_____________ km.
200
四、课堂检测
2.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆高度为(滑轮上方的部分忽略不计) ( )
A. 12 m B. 13 m C. 16 m D. 17 m
D
3. 在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( )
A. 8 B. 4 C. 6 D. 无法计算
A
四、课堂检测
4. 用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论正确的是( )
A. c2=a2+b2
B. c2=a2+2ab+b2
C. c2=a2-2ab+b2
D. c2=(a+b)2
A
5.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
四、课堂检测
四、课堂检测
解:在Rt△MNO中,
根据勾股定理,
∴OM?=MN?+NO?
=300?+400?
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
6.一个直角三角形的斜边为20cm,且两直角边的长度比为3︰4,求两直角边的长。
3x
4x
20
四、课堂检测
解:设这两直角边的长分别为3x cm和4x cm,根据勾股定理,得
∴(3x)?+(4x)?=20?
∴解得x=4
∴3x=3×4=12 cm,
4x=4×4=16 cm
答:这两直角边的长分别
为12 cm和16cm
7.如图,马路边一根高为5.4m的电线杆,被一辆卡车从离地面1.5m处撞断裂,倒下的电线杆顶部是否会落在离它的底部A处4m的快车道上?
A
B
C
C`
四、课堂检测
解:在Rt△ABC中,
AB=1.5 m,BC=5.4-1.5=3.9 m
根据勾股定理,得
∴AC?=BC?-AB?
=2.9?-1.5?
=12.96<4?
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
8.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
8
10
四、课堂检测
解:设EC为x cm,则DE为(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABC中,根据勾股定理,得
∴AC?=BC?-AB?
=2.9?-1.5?
=12.96<4?
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
D
A
B
C
E
F
8
10
四、课堂检测
解:设EC=x cm,则DE=(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABF中,根据勾股定理,得 ∴BF?=AF?-AB? =10?-8? =6?
∴BF=6 cm ∴FC=10-6=4 cm
在Rt△EFC中,根据勾股定理,得
∴ x?+42=(8-x)2
解得x=3
则EC=3 cm
9.如图,一个25 m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24 m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4 m吗?
A
B
O
C
D
四、课堂检测
A
B
O
C
D
四、课堂检测
解:在Rt△AOB中,根据勾股定理,得 ∴OB?=AB?-AO? =25?-24? =7?
∴OB=7 cm
在Rt△COD中,CD=AB=25cm
OC=OB-AC=24-4=20cm,
由勾股定理,得
∴OD?=CD?-OC? =25?-20? =15?
∴OD =15cm
∴ BD=15-7=8 cm
∴那么梯子底端B也外移8 m
10.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的卡车能通过隧道吗?
O
A
C
B
解:
过点A作AB⊥OC于点B,
∵∠ABO=90°
∴AB2+OB2=OA2
且OA=3.6,OB=1.5
∴AB2+1.52=3.62
∴AB2=10.71
∵AB2> 32
∴卡车能通过隧道
五、课堂小结
定理内容
勾股
定理
定理运用
重要的思想方法及数学思想
从特殊到一般、数形结合思想
六、布置作业
课本P6 习题1.2 第1,2,3题
谢谢聆听
第一章
勾股定理
1.1 探究勾股定理(二)
一、复习回顾
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,
一、复习回顾
我们是怎样发现“勾股定理”的?
割 -将正方形分割成4个全等直角三角形和1个小正方形
补-将正方形按图补成大正方形内部
一、复习回顾
你能用下列的图形验证勾股定理?
据不完全统计,验证的方法有400多种,你想得到自己的方法吗?
a2+b2=c2
二、探究新知
请利用边长分别为a,b,c的四个全等直角三角形拼出以斜边c为边长的正方形.
活动探究一:
有哪些拼法?
a
b
c
a
b
c
a
b
c
a
b
c
拼图展示
图 1
图 2
a
b
c
a
b
c
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
图 1
a
b
c
A
B
C
D
整体思想: S正ABCD =c2
部分思想: S正ABCD
验证方法一
图 2
a
b
c
验证方法二
如图1,你能把正方形ABCD的面积表示出来吗?有哪些表示方法?
整体思想:S正ABCD =c2
部分思想:S正ABCD
“勾股定理”的验证方法:
我们利用拼图的方法,将形的问题与数的问题结合起来,再进行整式运算,从理论上验证了勾股定理.
二、探究新知
观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2 。
延伸拓展
A
B
C
A的面积
SA
B的面积
SB
C的面积
SC
图1
图2
A
B
C
图1
图2
8
9
29
5
8
9
钝角三角形:a2+b2 < c2
锐角三角形:a2+b2 > c2
例1 我方侦察员小王在距离东西向公路400米处侦察,发现一辆敌方汽车在公路上疾驶。他赶紧拿出红外测距仪,测得汽车与他相距400米,10秒后,汽车与他相距500米,你能帮助小王计算敌方汽车的速度吗?
三、典例精析
解:在Rt△ABC中,根据勾股定理,
∴BC?=AB?-AC?
=500?-400?
=3002
∴BC=300 m
V敌方汽车=S÷t=300÷10=30 (m/s)
答:敌方汽车的速度为30 m/s
例2 如图,受台风“圆规”影响,一棵高18米的大树断裂,树的顶部落在离树根底部6米处,这棵树折断后有多高?
6米
x
18-x
三、典例精析
解:设这棵树折断后有x米高,则折断的部分为(18-x)米,根据勾股定理,得
∴x?+6?=(18-x)?
∴解得x=8 m
答:这棵树折断后有8米高
例3.如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
“总统证明法”
三、典例精析
S等腰直角三角形
S等腰直角三角形
1. 一艘船由于风向的原因先向正东方向航行了160 km,然后向正北方向航行了120 km,这时它离出发点有_____________ km.
200
四、课堂检测
2.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆高度为(滑轮上方的部分忽略不计) ( )
A. 12 m B. 13 m C. 16 m D. 17 m
D
3. 在Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为( )
A. 8 B. 4 C. 6 D. 无法计算
A
四、课堂检测
4. 用四个边长均为a,b,c的直角三角板,拼成如图所示的图形,则下列结论正确的是( )
A. c2=a2+b2
B. c2=a2+2ab+b2
C. c2=a2-2ab+b2
D. c2=(a+b)2
A
5.如图是某沿江地区交通图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速,已知沿江高速的建设成本是100万元/千米,该沿江高速的造价预计是多少?
四、课堂检测
四、课堂检测
解:在Rt△MNO中,
根据勾股定理,
∴OM?=MN?+NO?
=300?+400?
=5002
∴OM=500 km
同理,得 OQ=1300 km
∴沿江高速长为 OM+OQ=500 +1300=1800 km
∴该沿江高速的造价为 1800× 100=180000 万元
答:该沿江高速的造价预计是180000 万元
6.一个直角三角形的斜边为20cm,且两直角边的长度比为3︰4,求两直角边的长。
3x
4x
20
四、课堂检测
解:设这两直角边的长分别为3x cm和4x cm,根据勾股定理,得
∴(3x)?+(4x)?=20?
∴解得x=4
∴3x=3×4=12 cm,
4x=4×4=16 cm
答:这两直角边的长分别
为12 cm和16cm
7.如图,马路边一根高为5.4m的电线杆,被一辆卡车从离地面1.5m处撞断裂,倒下的电线杆顶部是否会落在离它的底部A处4m的快车道上?
A
B
C
C`
四、课堂检测
解:在Rt△ABC中,
AB=1.5 m,BC=5.4-1.5=3.9 m
根据勾股定理,得
∴AC?=BC?-AB?
=2.9?-1.5?
=12.96<4?
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
8.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
8
10
四、课堂检测
解:设EC为x cm,则DE为(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABC中,根据勾股定理,得
∴AC?=BC?-AB?
=2.9?-1.5?
=12.96<4?
答:倒下的电线杆顶部会落在离它的底部A处4m的快车道上
D
A
B
C
E
F
8
10
四、课堂检测
解:设EC=x cm,则DE=(8-x)cm
由折叠性质,得
AD=AF=10 cm
EF=DE=(8-x) cm
在Rt△ABF中,根据勾股定理,得 ∴BF?=AF?-AB? =10?-8? =6?
∴BF=6 cm ∴FC=10-6=4 cm
在Rt△EFC中,根据勾股定理,得
∴ x?+42=(8-x)2
解得x=3
则EC=3 cm
9.如图,一个25 m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24 m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4 m吗?
A
B
O
C
D
四、课堂检测
A
B
O
C
D
四、课堂检测
解:在Rt△AOB中,根据勾股定理,得 ∴OB?=AB?-AO? =25?-24? =7?
∴OB=7 cm
在Rt△COD中,CD=AB=25cm
OC=OB-AC=24-4=20cm,
由勾股定理,得
∴OD?=CD?-OC? =25?-20? =15?
∴OD =15cm
∴ BD=15-7=8 cm
∴那么梯子底端B也外移8 m
10.如图,某隧道的截面是一个半径为3.6米的半圆形,一辆高2.4米、宽3米的卡车能通过隧道吗?
O
A
C
B
解:
过点A作AB⊥OC于点B,
∵∠ABO=90°
∴AB2+OB2=OA2
且OA=3.6,OB=1.5
∴AB2+1.52=3.62
∴AB2=10.71
∵AB2> 32
∴卡车能通过隧道
五、课堂小结
定理内容
勾股
定理
定理运用
重要的思想方法及数学思想
从特殊到一般、数形结合思想
六、布置作业
课本P6 习题1.2 第1,2,3题
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
