第一章 勾股定理回顾与思考课件(共26张PPT)
文档属性
| 名称 | 第一章 勾股定理回顾与思考课件(共26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 00:00:00 | ||
图片预览





文档简介
2020年秋北师大版八年级上册
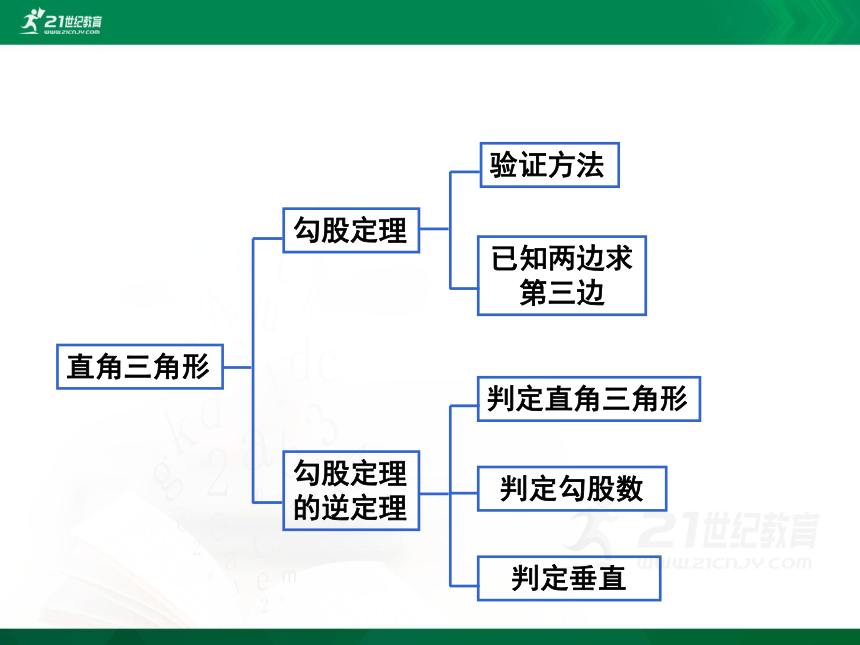
第一章
勾股定理
复习专题
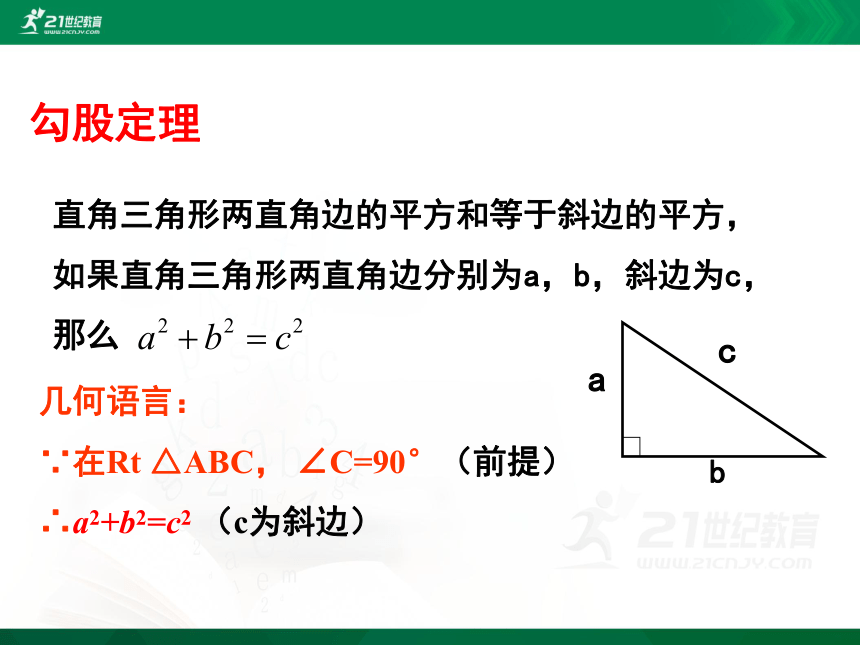
勾股定理
勾股定理
的逆定理
直角三角形
验证方法
已知两边求
第三边
判定直角三角形
判定勾股数
判定垂直
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,如果直角三角形两直角边分别为a,b,斜边为c,那么
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么
这个三角形是直角三角形
勾股定理的逆定理
注意:c为斜边,∠C为直角
a
b
c
A
C
B
∵在 △ABC中, a,b,c为三边长, c为最大边,且a2+b2=c2
∴∠C=90°
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
勾股定理
勾股定理逆定理
区别
联系
条件:一个三角形是直角三角形;
结论:三角形三边有a2+b2=c2关系
条件:一个三角形的三边a、b、c满足a2+b2=c2
结论:这个三角形是直角三角形
?都与三角形三边有关
?都与直角三角形有关
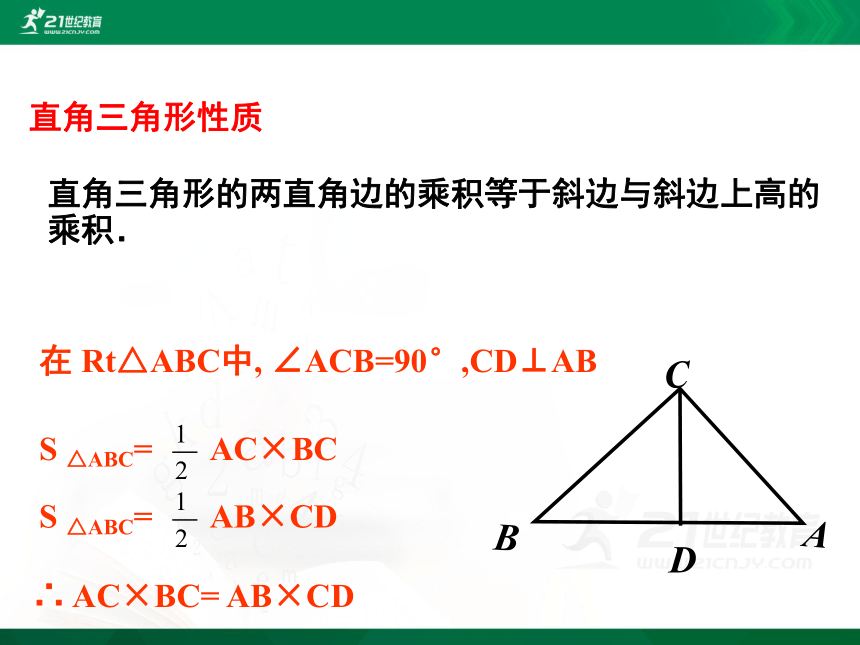
直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.
直角三角形性质
A
D
B
C
在 Rt△ABC中, ∠ACB=90°,CD⊥AB
S △ABC= AC×BC
S △ABC= AB×CD
∴ AC×BC= AB×CD
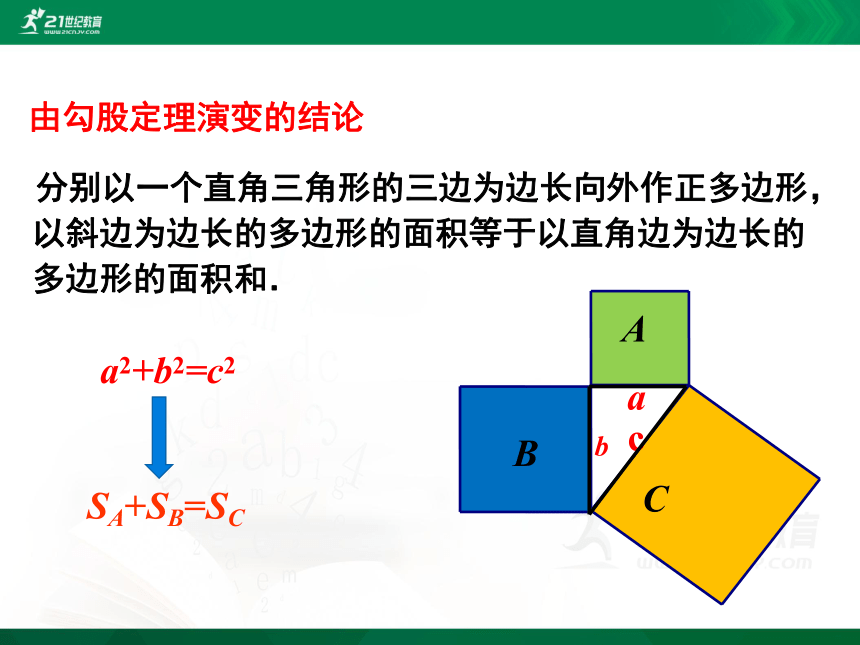
分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
由勾股定理演变的结论
A
B
a
c
b
C
SA+SB=SC
a2+b2=c2
应用:已知直角三角形的任意两边,利用勾股定理可以求出第三边.
注意以下几点:
①应用勾股定理的前提条件是在直角三角形中.
②应用勾股定理时,必须分清斜边和直角边.
③应用勾股定理时,如果没有直角三角形,可以通过添加辅助线的方式构造出直角三角形,再利用勾股定理来解答.
勾股定理的应用
平面展开﹣最短路径问题
(1)根据题意把立体图形展开成平面图形
(2)再确定两点之间的最短路径.一般情况是两点之间,线段最短.
(3)在平面图形上构造直角三角形解决问题.
勾股定理的应用
1.若一直角三角形两边长分别为12和5,则第三边长的平方为( )
169 B. 169或119 C. 119 D. 225
当第三边为斜边时,第三边长的平方=122+52=169;当第三边为直角边时,第三边长的平方=122-52=119.
B
典例精析
2. 下列各组数据是勾股数的有________. (填序号)
①6,8,10;
②10,6,14;
③0.3,0.4,0.5;
④7,24,25;
①④
3.如图,在高为3 m,斜坡长为5 m的楼梯台阶上铺地毯,则地毯的长度至少要( )
A. 4 m B. 5 m C. 6 m D. 7 m
D
典例精析
4. 在△ABC中,∠C=90°,c=10,a∶b=3∶4,则a=______,b=________.
.
6
8
5.如图是一个长方体,长4,宽3,高12,则图中阴影部分的三角形的周长为___ _.
30
典例精析
6.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB,BC,DC为边向外作正方形,其面积分别为S1,S2,S3,若S1=3,S3=9,则S2等于( )
12 B. 18
C. 24 D. 48
D
典例精析
7. 一架5 m的梯子,斜靠在一竖直的墙上,这时梯足距墙角3 m,若梯子的顶端下滑1 m,则梯足将滑动( )
A. 0 m B. 1 m C. 2 m D. 3 m
B
典例精析
8. 将一根长24 cm的筷子置于底面直径为15 cm,高8 cm的圆柱形水杯中,如图Z1-8.设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
A. h≤17
B. 7≤h≤16
C. 15≤h≤16
D. h≥8
B
典例精析
9.如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
典例精析
10.如图,小明的爸爸在鱼池边开了一块四边形土地种菜,爸爸让小明计算一下土地的面积,以便计算产量. 小明找了一卷米尺,测得AB=3 m,AD=4 m,CD=13 m,BC=12 m,又已知∠A=90°,求这块四边形ABCD土地的面积.
典例精析
解:如图,连接BD.
∵ ∠A=90°,
∴ BD2=AD2+AB2=25.
则BD2+BC2=25+144=169=132=CD2,
∴ ∠CBD=90°.
∴ S四边形=S△ADB+S△CBD
= AD·AB+ BD·BC
= ×4×3+ ×5×12
=36(m2).
典例精析
11.红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m. 如果沿CD修一条水渠且点D在边AB上,水渠的造价为10元/m,问点D在什么位置时,水渠的造价最低?最低造价是多少?
典例精析
解:∵AC=75 m,BC=100 m,AB=125 m,
∴AC2+BC2=752+1002=AB2=15 625.
∴∠ACB=90°.
当CD⊥AB时,水渠的造价最低.
此时由S△ABC=12AB·CD=12AC·BC,
得CD= =60(m).
故60×10=600(元).
答:当CD⊥AB时,水渠的造价最低,最低造价是600元.
典例精析
12.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6 m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4 m,距地面1.4 m,求秋千AB的长.
解:设AB=AB′=x,由题意可得
B′E=1.4-0.6=0.8(m),
则AE=AB-0.8=x-0.8.
在Rt△AEB中,
∵ AE2+BE2=AB2,
∴ (x-0.8)2+2.42=x2,解得x=4.
答:秋千AB的长为4 m.
典例精析
13. 一只螳螂在一圆柱形松树树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它. 已知树干横截面的周长为20 cm,A,B两点的距离为15 cm. 若螳螂想吃掉在点B的小虫子,求螳螂绕行的最短路程.
典例精析
解:把这段树干看成用纸卷成的圆柱,
从AB处将它展开如图,则AB即为所求的最短路程.
其中BA′=15 cm,AA′=20 cm,
在Rt△AA′B中,AA′2+BA′2=AB2,
即202+152=252=AB2.
所以AB=25(cm).
答:螳螂绕行的最短路程是25 cm.
典例精析
14. 如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形面积.
解:∵ ∠BAD=90°,
∴ AD2+AB2=DB2.
∴ 32+42=DB2,∴ DB=5.
∵ ∠CBD=90°,∴ BD2+BC2=DC2.
∴ 52+122=DC2.
∴ DC=13.
∴ S正方形DCEF=DC2=132=169.
典例精析
谢谢聆听
第一章
勾股定理
复习专题
勾股定理
勾股定理
的逆定理
直角三角形
验证方法
已知两边求
第三边
判定直角三角形
判定勾股数
判定垂直
勾股定理
几何语言:
∵在Rt △ABC, ∠C=90°(前提)
∴a2+b2=c2 (c为斜边)
a
b
c
直角三角形两直角边的平方和等于斜边的平方,如果直角三角形两直角边分别为a,b,斜边为c,那么
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么
这个三角形是直角三角形
勾股定理的逆定理
注意:c为斜边,∠C为直角
a
b
c
A
C
B
∵在 △ABC中, a,b,c为三边长, c为最大边,且a2+b2=c2
∴∠C=90°
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
勾股定理
勾股定理逆定理
区别
联系
条件:一个三角形是直角三角形;
结论:三角形三边有a2+b2=c2关系
条件:一个三角形的三边a、b、c满足a2+b2=c2
结论:这个三角形是直角三角形
?都与三角形三边有关
?都与直角三角形有关
直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.
直角三角形性质
A
D
B
C
在 Rt△ABC中, ∠ACB=90°,CD⊥AB
S △ABC= AC×BC
S △ABC= AB×CD
∴ AC×BC= AB×CD
分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
由勾股定理演变的结论
A
B
a
c
b
C
SA+SB=SC
a2+b2=c2
应用:已知直角三角形的任意两边,利用勾股定理可以求出第三边.
注意以下几点:
①应用勾股定理的前提条件是在直角三角形中.
②应用勾股定理时,必须分清斜边和直角边.
③应用勾股定理时,如果没有直角三角形,可以通过添加辅助线的方式构造出直角三角形,再利用勾股定理来解答.
勾股定理的应用
平面展开﹣最短路径问题
(1)根据题意把立体图形展开成平面图形
(2)再确定两点之间的最短路径.一般情况是两点之间,线段最短.
(3)在平面图形上构造直角三角形解决问题.
勾股定理的应用
1.若一直角三角形两边长分别为12和5,则第三边长的平方为( )
169 B. 169或119 C. 119 D. 225
当第三边为斜边时,第三边长的平方=122+52=169;当第三边为直角边时,第三边长的平方=122-52=119.
B
典例精析
2. 下列各组数据是勾股数的有________. (填序号)
①6,8,10;
②10,6,14;
③0.3,0.4,0.5;
④7,24,25;
①④
3.如图,在高为3 m,斜坡长为5 m的楼梯台阶上铺地毯,则地毯的长度至少要( )
A. 4 m B. 5 m C. 6 m D. 7 m
D
典例精析
4. 在△ABC中,∠C=90°,c=10,a∶b=3∶4,则a=______,b=________.
.
6
8
5.如图是一个长方体,长4,宽3,高12,则图中阴影部分的三角形的周长为___ _.
30
典例精析
6.如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB,BC,DC为边向外作正方形,其面积分别为S1,S2,S3,若S1=3,S3=9,则S2等于( )
12 B. 18
C. 24 D. 48
D
典例精析
7. 一架5 m的梯子,斜靠在一竖直的墙上,这时梯足距墙角3 m,若梯子的顶端下滑1 m,则梯足将滑动( )
A. 0 m B. 1 m C. 2 m D. 3 m
B
典例精析
8. 将一根长24 cm的筷子置于底面直径为15 cm,高8 cm的圆柱形水杯中,如图Z1-8.设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
A. h≤17
B. 7≤h≤16
C. 15≤h≤16
D. h≥8
B
典例精析
9.如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为________cm(杯壁厚度不计).
20
典例精析
10.如图,小明的爸爸在鱼池边开了一块四边形土地种菜,爸爸让小明计算一下土地的面积,以便计算产量. 小明找了一卷米尺,测得AB=3 m,AD=4 m,CD=13 m,BC=12 m,又已知∠A=90°,求这块四边形ABCD土地的面积.
典例精析
解:如图,连接BD.
∵ ∠A=90°,
∴ BD2=AD2+AB2=25.
则BD2+BC2=25+144=169=132=CD2,
∴ ∠CBD=90°.
∴ S四边形=S△ADB+S△CBD
= AD·AB+ BD·BC
= ×4×3+ ×5×12
=36(m2).
典例精析
11.红星中学计划把一块形状如图所示的废弃荒地开辟为生物园,测得AC=75m,BC=100m,AB=125m. 如果沿CD修一条水渠且点D在边AB上,水渠的造价为10元/m,问点D在什么位置时,水渠的造价最低?最低造价是多少?
典例精析
解:∵AC=75 m,BC=100 m,AB=125 m,
∴AC2+BC2=752+1002=AB2=15 625.
∴∠ACB=90°.
当CD⊥AB时,水渠的造价最低.
此时由S△ABC=12AB·CD=12AC·BC,
得CD= =60(m).
故60×10=600(元).
答:当CD⊥AB时,水渠的造价最低,最低造价是600元.
典例精析
12.如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6 m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4 m,距地面1.4 m,求秋千AB的长.
解:设AB=AB′=x,由题意可得
B′E=1.4-0.6=0.8(m),
则AE=AB-0.8=x-0.8.
在Rt△AEB中,
∵ AE2+BE2=AB2,
∴ (x-0.8)2+2.42=x2,解得x=4.
答:秋千AB的长为4 m.
典例精析
13. 一只螳螂在一圆柱形松树树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它. 已知树干横截面的周长为20 cm,A,B两点的距离为15 cm. 若螳螂想吃掉在点B的小虫子,求螳螂绕行的最短路程.
典例精析
解:把这段树干看成用纸卷成的圆柱,
从AB处将它展开如图,则AB即为所求的最短路程.
其中BA′=15 cm,AA′=20 cm,
在Rt△AA′B中,AA′2+BA′2=AB2,
即202+152=252=AB2.
所以AB=25(cm).
答:螳螂绕行的最短路程是25 cm.
典例精析
14. 如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,求以DC为边的正方形面积.
解:∵ ∠BAD=90°,
∴ AD2+AB2=DB2.
∴ 32+42=DB2,∴ DB=5.
∵ ∠CBD=90°,∴ BD2+BC2=DC2.
∴ 52+122=DC2.
∴ DC=13.
∴ S正方形DCEF=DC2=132=169.
典例精析
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
