1.2 一定是直角三角形吗课件(共26张PPT)
文档属性
| 名称 | 1.2 一定是直角三角形吗课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 22:06:51 | ||
图片预览






文档简介
2020年秋北师大版八年级上册
第一章
勾股定理
1.2 一定是直角三角形吗
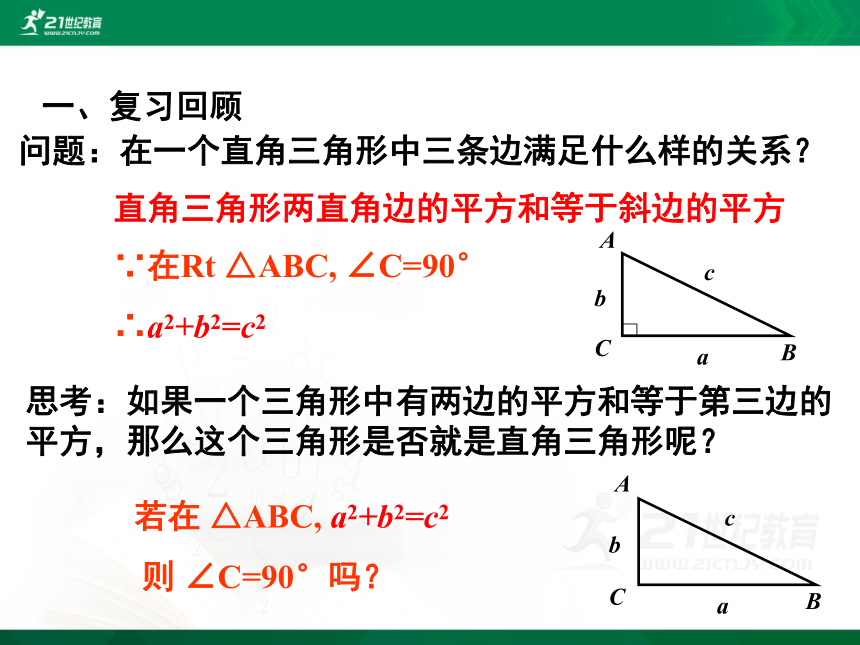
一、复习回顾
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
a
b
c
A
C
B
问题:在一个直角三角形中三条边满足什么样的关系?
思考:如果一个三角形中有两边的平方和等于第三边的 平方,那么这个三角形是否就是直角三角形呢?
若在 △ABC, a2+b2=c2
则 ∠C=90°吗?
a
b
c
A
C
B
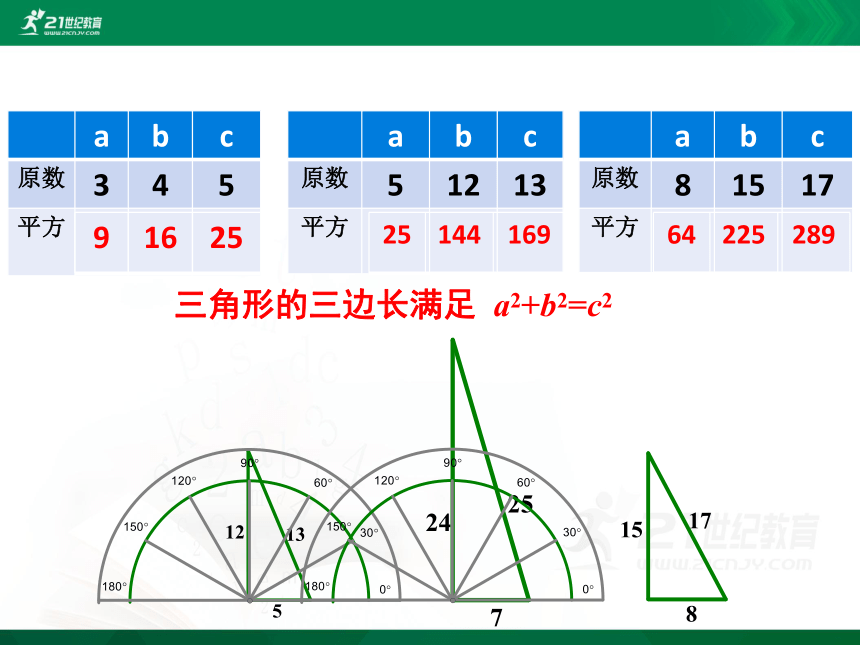
三角形的三边长a,b,c分别为下面的每组数:
① 3,4,5; ② 5,12,13; ③8,15,17.
1.请问下列的三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
二、探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
3
4
5
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
5
12
13
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
8
15
17
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}9
16
25
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}25
144
169
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}64
225
289
三角形的三边长满足 a2+b2=c2
你发现了有什么样的结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
你能证明吗?
a
b
c
A
C
B
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
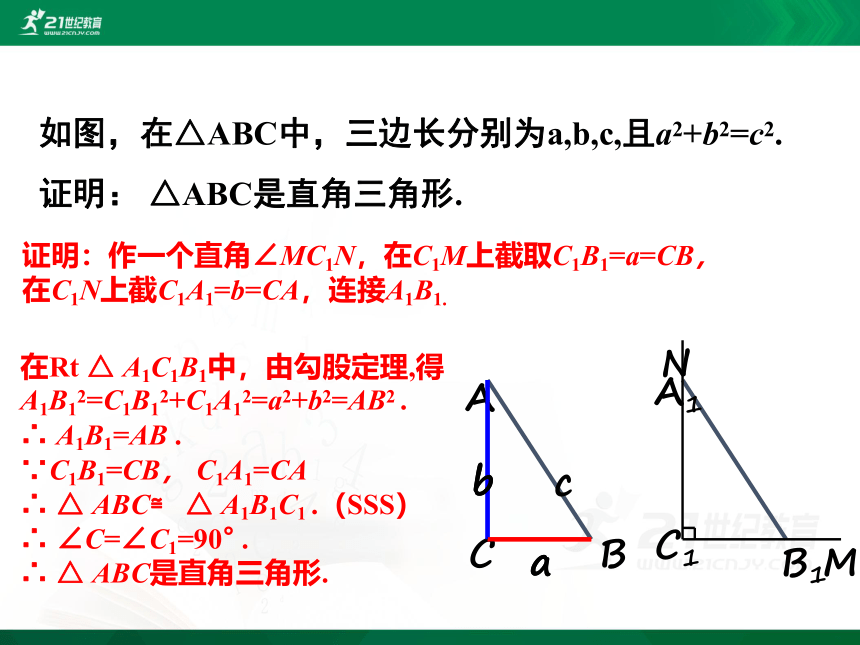
如图,在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
证明: △ABC是直角三角形.
证明:作一个直角∠MC1N,在C1M上截取C1B1=a=CB,在C1N上截C1A1=b=CA,连接A1B1.
在Rt △ A1C1B1中,由勾股定理,得
A1B12=C1B12+C1A12=a2+b2=AB2 .
∴ A1B1=AB .
∵C1B1=CB, C1A1=CA
∴ △ ABC≌ △ A1B1C1 .(SSS)
∴ ∠C=∠C1=90° .
∴ △ ABC是直角三角形.
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么
这个三角形是直角三角形
勾股定理的逆定理
注意:c为斜边,∠C为直角
a
b
c
A
C
B
∵在 △ABC中, a,b,c为三边长, c为最大边,且a2+b2=c2
∴∠C=90°
应用:用于判定直角三角形
提问:通过今天探究,你能体验出一个数学结论的发现往往要经历哪些过程?
数学结论的发现总是要经历观察、归纳、猜想和验证的过程,同时遵循由“特殊—一般—特殊”的发展规律.
勾股数
满足a2 +b2 =c2的三个正整数,称为勾股数.
常见的勾股数:
3,4, 5; 5,12,13; 6,8,10;
7,24,25; 8,15,17;
勾股数的正整数倍仍然是勾股数
注意: ①三个数是正整数;
② 三个数满足a2 +b2 =c2
(1)如果△ABC的三边长分别为a,b,c,且满足a2=b2-c2,则△ABC为直角三角形 ( )
(2)以△ABC三边分别向外作正方形,它们的面积分别是S1,S2,S3,如果S1+S2=S3,则△ABC为直角三角形 ( )
(3)如果△ABC的三边长分别为a,b,c,且满足a2 +c2=b2,则∠C是直角 ( )
三、典例精析
√
√
√
1.判断下列的说法
2.下列条件中判断△ABC不是直角三角形的是 ( )
A. AB=3,BC=4,AC=5
B. AB=9,BC=40,AC=41
C. AB=7,BC=8,AC=25
D. AB=5,BC=12,AC=13
C
三、典例精析
3.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
三、典例精析
解:符合要求,
∵ 在△ABD中,AB2+AD2=32+42=52=BD2
∴∠A=90°,
又∵在△BCD中, BD2+BC2=52+122=132=CD2
∴ ∠DBC=90°
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
1.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
△ABE,△DEF,△FCB均为直角三角形,由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是直角三角形
变式训练
1. 下列各组数中,不是勾股数的是 ( )
A. 0.3,0.4,0.5 B. 9,40,41
C. 6,8,10 D. 7,24,25
A
四、课堂检测
注意: ①三个数是正整数;
② 三个数满足a2 +b2 =c2
2. 下面各组数中,不能构成直角三角形三边长的一组数是( )
A. 3,4,5 B. 6,8,10
C. 5,12,13 D. 8,12,15
D
3. 如图所示正方形网格中的△ABC,若小方的格边长为1,则△ABC的形状为 ( )
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 以上答案都不对
A
四、课堂检测
4.将直角三角形的三边同时扩大相同的倍数后,得到的三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
四、课堂检测
A
5. △ABC的三边分别是a,b,c且满足|a-8 |+(b-6)2=0,则当c2=__________时,△ABC是直角三角形.
100或28
6. 有四个三角形,分别满足下列条件:
①其中一个内角等于另外两个内角之和;
②三个内角之比为3∶4∶5;
③三边之比为3∶4∶5;
④三边长分别为5,24,25.
其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
B
四、课堂检测
7.在△ABC中,AC=15cm,BC=20cm ,AB=25cm ,则这个三角形的面积是多少?
四、课堂检测
A
C
B
解:(1) ∵ AC=15cm,BC=20cm ,AB=25cm
∴AC2+BC2=152+202=252=AB2
∴ △ABC是直角三角形.
S△ABC=15×20÷2=150(cm2)
8. 如图,AD⊥BC,垂足为点D. 如果CD=1,AD=2,BD=4.
△ABC是直角三角形吗?说明理由.
解:(1) ∵CD=1,AD=2,BD=4,AD⊥BC,
∴AC2=AD2+AC2=4+1=5,
AB2=AD2+BD2=4+16=20.
BC=CD+BD=5,
∴ AC2+AB2=5+20=25=BC2.
∴ △ABC是直角三角形.
四、课堂检测
四、课堂检测
9. 已知△ ABC的三边长a,b,c满足a=m2-n2,b=2mn,c=m2+n2,其中m,n是正整数,且m>n,判断△ABC的形状;
解: ∵ m>1,∴ a,b,c都是正整数,且c是最大边.
∴a2=(m2-n2)2= m4-2m2n2+n4 ,
b2=(2mn) 2= 4m2n2
c2=(m2+n2)2= m4+2m2n2+n4
∴ a2+ b2 = c2.
∴ △ABC是直角三角形.
10.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向行?
A
B
C
北
解:由题意画出相应的图形
AB=240海里,BC=70海里,AC=250海里;
在△ABC中,勾股定理,得
AC2-AB2=2502-2402
=(250+240)(250-240)
=4900=702=BC2
即AB2+BC2=AC2
∴△ABC是直角三角形
答:船转弯后,是沿正西方向航行的
A
B
C
北
五、课堂小结
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2. 勾股数:满足a2 +b2=c2的三个正整数, 称为勾股数.
六、布置作业
课本P10 习题1.3 第1,2,3,4题
谢谢聆听
第一章
勾股定理
1.2 一定是直角三角形吗
一、复习回顾
∵在Rt △ABC, ∠C=90°
∴a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方
a
b
c
A
C
B
问题:在一个直角三角形中三条边满足什么样的关系?
思考:如果一个三角形中有两边的平方和等于第三边的 平方,那么这个三角形是否就是直角三角形呢?
若在 △ABC, a2+b2=c2
则 ∠C=90°吗?
a
b
c
A
C
B
三角形的三边长a,b,c分别为下面的每组数:
① 3,4,5; ② 5,12,13; ③8,15,17.
1.请问下列的三组数都满足 a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
二、探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
3
4
5
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
5
12
13
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
a
b
c
原数
8
15
17
平方
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}9
16
25
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}25
144
169
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}64
225
289
三角形的三边长满足 a2+b2=c2
你发现了有什么样的结论吗?
如果三角形的三边长a,b,c满足a2+b2=c2,
那么这个三角形是直角三角形.
你能证明吗?
a
b
c
A
C
B
a
c
b
A
C
B
b
a
C1
M
N
B1
A1
如图,在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
证明: △ABC是直角三角形.
证明:作一个直角∠MC1N,在C1M上截取C1B1=a=CB,在C1N上截C1A1=b=CA,连接A1B1.
在Rt △ A1C1B1中,由勾股定理,得
A1B12=C1B12+C1A12=a2+b2=AB2 .
∴ A1B1=AB .
∵C1B1=CB, C1A1=CA
∴ △ ABC≌ △ A1B1C1 .(SSS)
∴ ∠C=∠C1=90° .
∴ △ ABC是直角三角形.
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么
这个三角形是直角三角形
勾股定理的逆定理
注意:c为斜边,∠C为直角
a
b
c
A
C
B
∵在 △ABC中, a,b,c为三边长, c为最大边,且a2+b2=c2
∴∠C=90°
应用:用于判定直角三角形
提问:通过今天探究,你能体验出一个数学结论的发现往往要经历哪些过程?
数学结论的发现总是要经历观察、归纳、猜想和验证的过程,同时遵循由“特殊—一般—特殊”的发展规律.
勾股数
满足a2 +b2 =c2的三个正整数,称为勾股数.
常见的勾股数:
3,4, 5; 5,12,13; 6,8,10;
7,24,25; 8,15,17;
勾股数的正整数倍仍然是勾股数
注意: ①三个数是正整数;
② 三个数满足a2 +b2 =c2
(1)如果△ABC的三边长分别为a,b,c,且满足a2=b2-c2,则△ABC为直角三角形 ( )
(2)以△ABC三边分别向外作正方形,它们的面积分别是S1,S2,S3,如果S1+S2=S3,则△ABC为直角三角形 ( )
(3)如果△ABC的三边长分别为a,b,c,且满足a2 +c2=b2,则∠C是直角 ( )
三、典例精析
√
√
√
1.判断下列的说法
2.下列条件中判断△ABC不是直角三角形的是 ( )
A. AB=3,BC=4,AC=5
B. AB=9,BC=40,AC=41
C. AB=7,BC=8,AC=25
D. AB=5,BC=12,AC=13
C
三、典例精析
3.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
三、典例精析
解:符合要求,
∵ 在△ABD中,AB2+AD2=32+42=52=BD2
∴∠A=90°,
又∵在△BCD中, BD2+BC2=52+122=132=CD2
∴ ∠DBC=90°
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
1.如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,你是如何判断的?
4
1
2
2
4
3
△ABE,△DEF,△FCB均为直角三角形,由勾股定理知
BE2=22+42=20,EF2=22+12=5,
BF2=32+42=25
∴BE2+EF2=BF2
∴ △BEF是直角三角形
变式训练
1. 下列各组数中,不是勾股数的是 ( )
A. 0.3,0.4,0.5 B. 9,40,41
C. 6,8,10 D. 7,24,25
A
四、课堂检测
注意: ①三个数是正整数;
② 三个数满足a2 +b2 =c2
2. 下面各组数中,不能构成直角三角形三边长的一组数是( )
A. 3,4,5 B. 6,8,10
C. 5,12,13 D. 8,12,15
D
3. 如图所示正方形网格中的△ABC,若小方的格边长为1,则△ABC的形状为 ( )
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 以上答案都不对
A
四、课堂检测
4.将直角三角形的三边同时扩大相同的倍数后,得到的三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.不能确定
四、课堂检测
A
5. △ABC的三边分别是a,b,c且满足|a-8 |+(b-6)2=0,则当c2=__________时,△ABC是直角三角形.
100或28
6. 有四个三角形,分别满足下列条件:
①其中一个内角等于另外两个内角之和;
②三个内角之比为3∶4∶5;
③三边之比为3∶4∶5;
④三边长分别为5,24,25.
其中直角三角形有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
B
四、课堂检测
7.在△ABC中,AC=15cm,BC=20cm ,AB=25cm ,则这个三角形的面积是多少?
四、课堂检测
A
C
B
解:(1) ∵ AC=15cm,BC=20cm ,AB=25cm
∴AC2+BC2=152+202=252=AB2
∴ △ABC是直角三角形.
S△ABC=15×20÷2=150(cm2)
8. 如图,AD⊥BC,垂足为点D. 如果CD=1,AD=2,BD=4.
△ABC是直角三角形吗?说明理由.
解:(1) ∵CD=1,AD=2,BD=4,AD⊥BC,
∴AC2=AD2+AC2=4+1=5,
AB2=AD2+BD2=4+16=20.
BC=CD+BD=5,
∴ AC2+AB2=5+20=25=BC2.
∴ △ABC是直角三角形.
四、课堂检测
四、课堂检测
9. 已知△ ABC的三边长a,b,c满足a=m2-n2,b=2mn,c=m2+n2,其中m,n是正整数,且m>n,判断△ABC的形状;
解: ∵ m>1,∴ a,b,c都是正整数,且c是最大边.
∴a2=(m2-n2)2= m4-2m2n2+n4 ,
b2=(2mn) 2= 4m2n2
c2=(m2+n2)2= m4+2m2n2+n4
∴ a2+ b2 = c2.
∴ △ABC是直角三角形.
10.一艘在海上朝正北方向航行的轮船,在航行240海里时方位仪坏了,凭经验,船长指挥船左传90°,继续航行70海里,则距出发地250海里,你能判断船转弯后,是否沿正西方向行?
A
B
C
北
解:由题意画出相应的图形
AB=240海里,BC=70海里,AC=250海里;
在△ABC中,勾股定理,得
AC2-AB2=2502-2402
=(250+240)(250-240)
=4900=702=BC2
即AB2+BC2=AC2
∴△ABC是直角三角形
答:船转弯后,是沿正西方向航行的
A
B
C
北
五、课堂小结
1.如果三角形的三边长a,b,c满足a2 +b2=c2,那么这个三角形是直角三角形.
2. 勾股数:满足a2 +b2=c2的三个正整数, 称为勾股数.
六、布置作业
课本P10 习题1.3 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
