2.1.2 认识无理数课件(共18张PPT)
文档属性
| 名称 | 2.1.2 认识无理数课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 22:14:17 | ||
图片预览



文档简介
2020年秋北师大版八年级上册
第二章
实数
2.1 认识无理数(一)
一、情景导入
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
二、探究新知
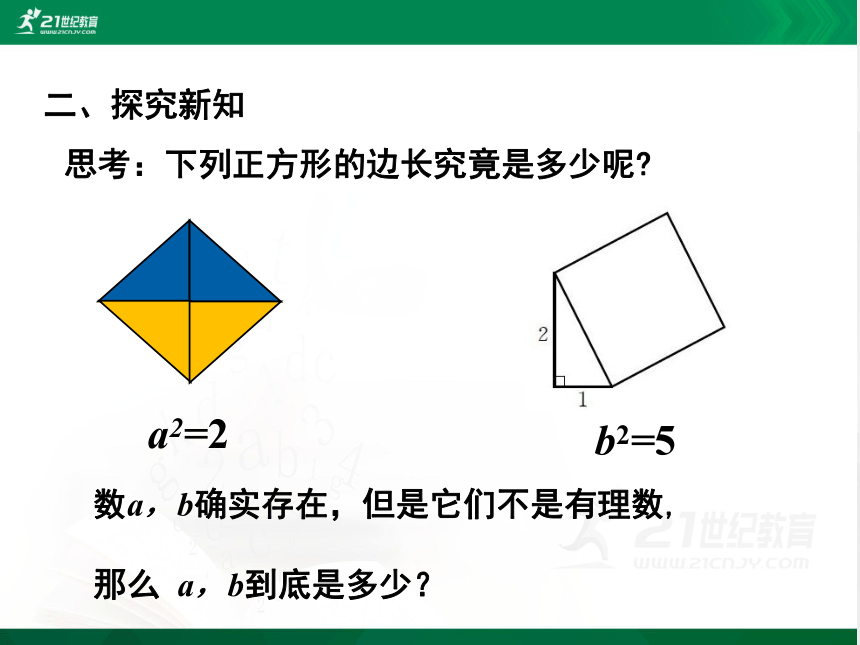
a2=2
b2=5
数a,b确实存在,但是它们不是有理数,
那么 a,b到底是多少?
思考:下列正方形的边长究竟是多少呢?
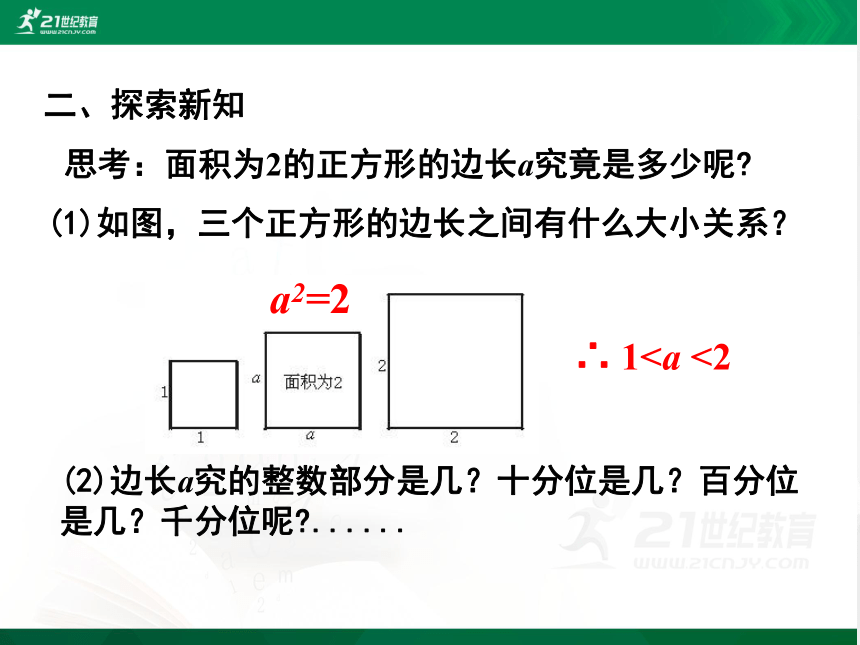
思考:面积为2的正方形的边长a究竟是多少呢?
二、探索新知
a2=2
∴ 1(2)边长a究的整数部分是几?十分位是几?百分位是几?千分位呢?......
(1)如图,三个正方形的边长之间有什么大小关系?
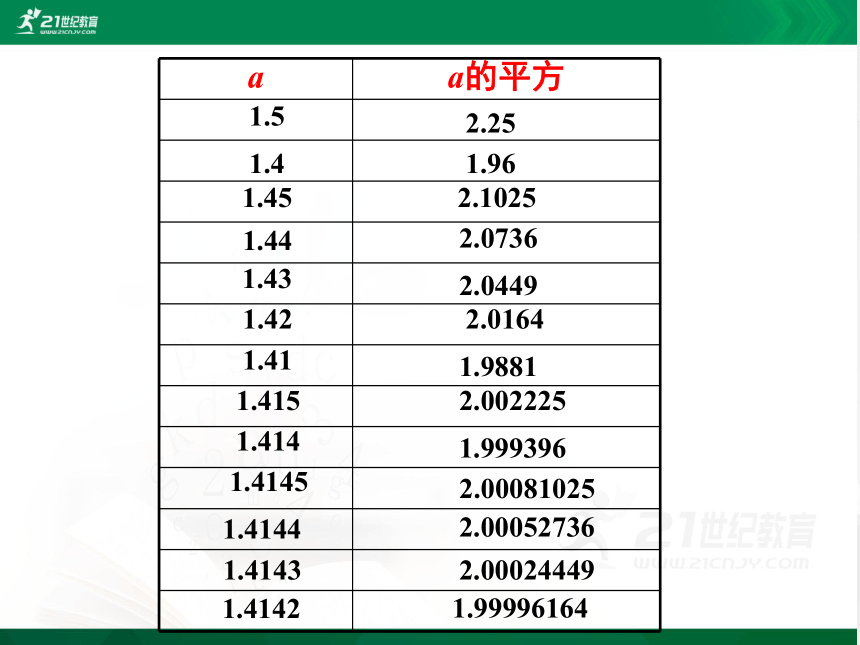
a
a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
边长a
面积s
111.41.961.411.98811.4141.9993961.41421.99996164a2=2 中的a是多少?
思考:还可以继续算下去吗?a可能是有限小数吗?
事实上,a =1.41421356…它是一个无限不循环小数
请大家用上面的方法估计面积为5的正方形的边长b的值. (b2=5,探索b是多少)
面积为2的正方形的边长a究竟是多少呢?
二、探索新知
实数上,b=2.23606797…它是一个无限不循环小数
结论:
a ,b不是整数,也不是分数,是无限不循环小数。
活动二:
把下列各数表示成小数,你发现了什么?
有理数
二、探索新知
分数化成小数,小数的形式有几种情况?
3=3.0;
有限小数
无限循环小数
即任何有限小数或无限循环小数都是有理数.
二、探索新知
有限小数
限循环小数
有理数
a =1.41421356…
b =2.23606797…
无限不循环小数
无限不循环小数称为无理数
像0.585885888588885…(相邻两个5之间8的个数逐次加1)
π=3.14159265,1.41421356…,-2.2360679…
等这些数的小数位数都是无限的,,又不是循环的,
而是无限不循环小数.
★ π是无限不循环小数,是无理数
二、探索新知
无限不循环小数叫无理数
二、探索新知
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数
无理数
★无理数一定是无限小数
无限小数不一定是无理数
1. 下列结论正确的是 ( )
A. 无限小数是无理数B. 无限不循环小数是无理数
C. 有理数就是有限小数D. 无理数就是开方开不尽的数
B
三、典例讲解
2.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
C
3. 将下列各数填在相应的集合中:
0.351, , ,3.141 59,6,
-5.232 333 2…, ,1.234 567 891 011…(由相继的正整数组成).
三、典例讲解
1.下列各数不是有理数的是 ( )
A. 3.14 B. 0
C. -0.101 001 000… D. -4
C
四、课堂检测
2. 下列说法正确的是 ( )
A. 0.121221222…是有理数
B. 无限小数都是无理数
C. 半径为3的圆周长是有理数
D. 无理数是无限小数
D
3.将下列的数进行分类:
-1, ,3.14,-π,3.3,0,2, ,0.181818…,0.202 002 000 2…(相邻两个2之间0的个数逐次加1).
有理数:___________________________________,
无理数:_________________________________.
-π,0.202 002 000 2…
四、课堂检测
五、课堂小结
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数 形式
( p≠0, p,q 为整数且互质)
而无理数则不能.
六、布置作业
课本P25习题2.2 第1、2、3、4题
谢谢聆听
第二章
实数
2.1 认识无理数(一)
一、情景导入
整数和分数统称为有理数
有理数
整数
分数
有理数
正有理数
负有理数
0
二、探究新知
a2=2
b2=5
数a,b确实存在,但是它们不是有理数,
那么 a,b到底是多少?
思考:下列正方形的边长究竟是多少呢?
思考:面积为2的正方形的边长a究竟是多少呢?
二、探索新知
a2=2
∴ 1(2)边长a究的整数部分是几?十分位是几?百分位是几?千分位呢?......
(1)如图,三个正方形的边长之间有什么大小关系?
a
a的平方
2.25
1.96
2.1025
2.0449
2.0736
2.0164
1.9881
2.002225
1.999396
2.00052736
2.00024449
1.99996164
2.00081025
1.4
1.5
1.45
1.44
1.43
1.42
1.41
1.415
1.414
1.4145
1.4144
1.4143
1.4142
边长a
面积s
1
思考:还可以继续算下去吗?a可能是有限小数吗?
事实上,a =1.41421356…它是一个无限不循环小数
请大家用上面的方法估计面积为5的正方形的边长b的值. (b2=5,探索b是多少)
面积为2的正方形的边长a究竟是多少呢?
二、探索新知
实数上,b=2.23606797…它是一个无限不循环小数
结论:
a ,b不是整数,也不是分数,是无限不循环小数。
活动二:
把下列各数表示成小数,你发现了什么?
有理数
二、探索新知
分数化成小数,小数的形式有几种情况?
3=3.0;
有限小数
无限循环小数
即任何有限小数或无限循环小数都是有理数.
二、探索新知
有限小数
限循环小数
有理数
a =1.41421356…
b =2.23606797…
无限不循环小数
无限不循环小数称为无理数
像0.585885888588885…(相邻两个5之间8的个数逐次加1)
π=3.14159265,1.41421356…,-2.2360679…
等这些数的小数位数都是无限的,,又不是循环的,
而是无限不循环小数.
★ π是无限不循环小数,是无理数
二、探索新知
无限不循环小数叫无理数
二、探索新知
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数
无理数
★无理数一定是无限小数
无限小数不一定是无理数
1. 下列结论正确的是 ( )
A. 无限小数是无理数B. 无限不循环小数是无理数
C. 有理数就是有限小数D. 无理数就是开方开不尽的数
B
三、典例讲解
2.下列一组数:-8,2.5,30,π, 0.161616 … ,0.6,0.080 080 008…(相邻两个8之间依次增加一个0),其中无理数有 ( )
A.0个 B.1个 C.2个 D.3个
C
3. 将下列各数填在相应的集合中:
0.351, , ,3.141 59,6,
-5.232 333 2…, ,1.234 567 891 011…(由相继的正整数组成).
三、典例讲解
1.下列各数不是有理数的是 ( )
A. 3.14 B. 0
C. -0.101 001 000… D. -4
C
四、课堂检测
2. 下列说法正确的是 ( )
A. 0.121221222…是有理数
B. 无限小数都是无理数
C. 半径为3的圆周长是有理数
D. 无理数是无限小数
D
3.将下列的数进行分类:
-1, ,3.14,-π,3.3,0,2, ,0.181818…,0.202 002 000 2…(相邻两个2之间0的个数逐次加1).
有理数:___________________________________,
无理数:_________________________________.
-π,0.202 002 000 2…
四、课堂检测
五、课堂小结
1.无理数是无限不循环小数,
有理数是有限小数或无限循环小数.
2.任何一个有理数都可以化成分数 形式
( p≠0, p,q 为整数且互质)
而无理数则不能.
六、布置作业
课本P25习题2.2 第1、2、3、4题
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
