2.2.1 平方根课件(共22张PPT)
文档属性
| 名称 | 2.2.1 平方根课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-29 22:18:28 | ||
图片预览







文档简介
2020年秋北师大版八年级上册
第二章
实数
2.2 平方根(一)
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
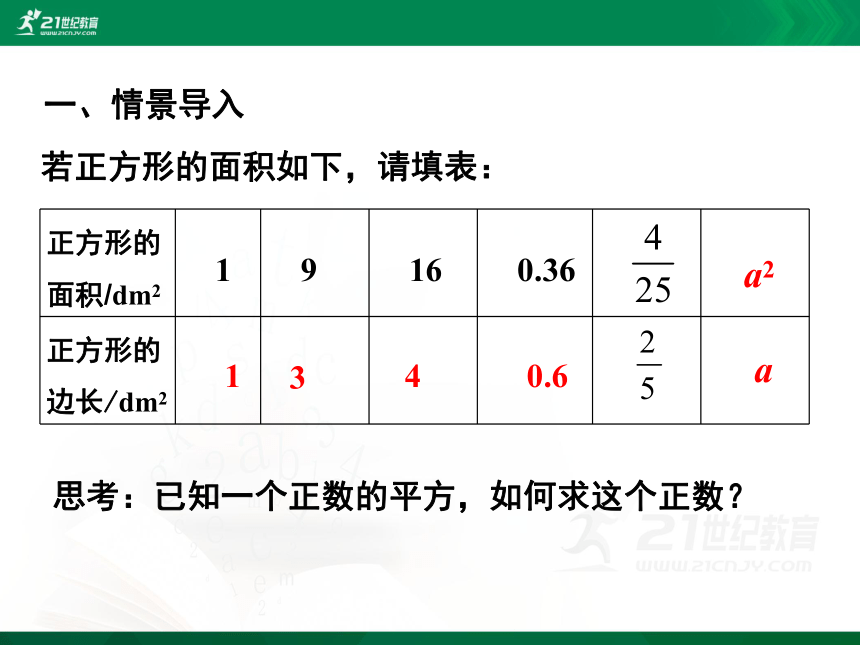
一、情景导入
若正方形的面积如下,请填表:
思考:已知一个正数的平方,如何求这个正数?
正方形的面积/dm2
1
9
16
0.36
正方形的边长/dm2
一、情景导入
4
0.6
3
1
a2
a
例: ∵ 52=25,
∴ 5是25的算术平方根,即
二、探究新知
(一)概念学习
定义:如果一个正数x的平方等于a,即x2=a ,
那么这个正数x就叫做a的算术平方根.
(1)记作: ,读作:根号a
(2)规定:0的算术平方根是0,
(3) 表示求a的算术平方根
例1:求下列各数的算术平方根
(1)900; (2)1; (3) ; (4)0.04; (5)14
三、典例讲解
解:(1)∵ 302=900,
∴ 900是30的算术平方根,即
(2)∵ 12=1,
∴ 1是1的算术平方根,即
例1:求下列各数的算术平方根
(1)900; (2)1; (3) ; (4)0.04; (5)14
三、典例讲解
(4)∵ (0.2)2=0.04,
∴ 0.04是0.2的算术平方根,即
解:(3)∵ 2=
∴ 900是30的算术平方根,即
(5) 14的算术平方根,即
例2:求下各列的值
三、典例讲解
解:(1)∵ 82=64, ∴
(2)∵(0.7)2=0.49, ∴
(3)∵( )2 = , ∴
(4)∵ 132 = 169 , ∴
思考:
(1)-4有算术平方根吗?即有一个正数的平方等于-4吗?
(2)什么数才有算术平方根?
负数没有算术平方根;非负数才有算术平方根
(1)正数有一个正的算术平方根;
(2)0的算术平方根是0;
(3)负数没有算术平方根;
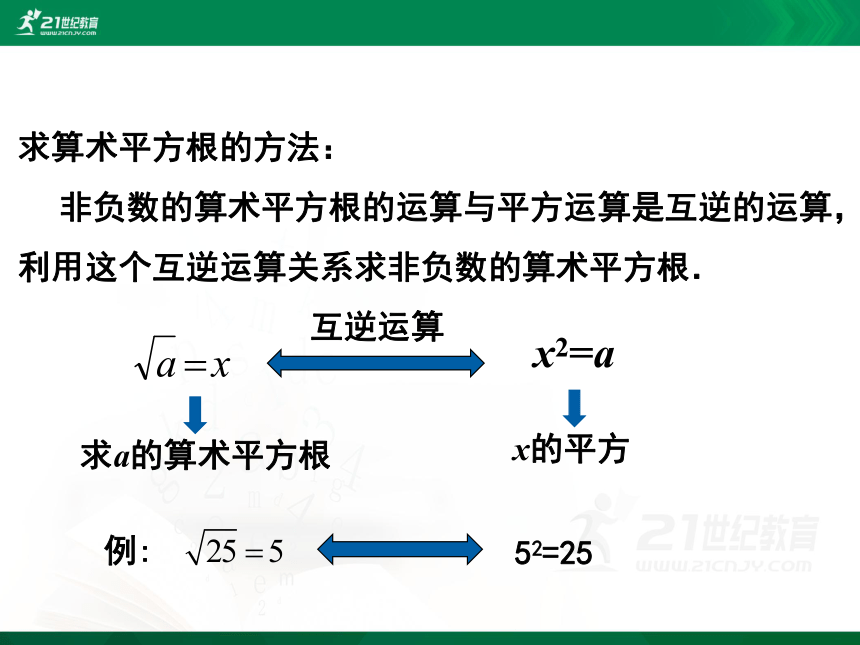
求算术平方根的方法:
非负数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
求a的算术平方根
x2=a
x的平方
互逆运算
例:
52=25
三、典例讲解
例3: 的算术平方根是 .
3
表示求a的算术平方根
的算术平方根是 .
a ≥ 0
(1)非负数才有算术平方根
≥ 0
(2)非负数的算术平方根是非负数
负数不存在算术平方根,
即当 a<0时, 无意义
式子 中的双重非负性:
(1)a≥0;
(2) ≥0.
算术平方根的性质:
判断:下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:(1)a=-4 <0,式子无意义;
(4)a=-(-5)=5 > 0,式子有意义.
(3)a=(-3)2=9 > 0,式子有意义;
(2)a=4 > 0,式子有意义;
三、典例讲解
例4:
若|a-3|+
的值为 。
,则代数式
-1
|a-3|≥0
≥0
∵ |a-3|+
a-3=0, b+4=0
a=3, b=-4
例5:自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9 t2.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
h=4.9 t2,
得 t2 =4,所以t =2(秒).
即铁球到达地面需要2秒.
三、典例讲解
1.16的算术平方根是 ( )
A. 2 B. 4 C. ±2 D. ±4
A
四、课堂检测
2. 2的算术平方根是 ( )
C
3.一个数的算术平方根是3,则这个数是( )
A. 3 B. 6
C. 9 D.
C
4.下列说法正确的是( )
A. 5是25的算术平方根B. -6是36的算术平方根
C. 0的算术平方根是0 D. 0.01是0.1的算术平方根
四、课堂检测
B
5. 下列各式表示正确的是 ( )
D
6. 小明房间的面积为10.8 m2,房间地面恰好由120块相同的正方形地砖铺成,则每块地砖的边长是 ( )
A. 0.3 m B. 0.45 m
C. 0.9 m D. 0.09 m
A
四、课堂检测
7. 下列结论正确的是 ( )
A
8. 若 ,则a=________;若 ,则a=__________.
10
-1
四、课堂检测
9.已知:|x+2y|+ +(5y+z)2=0
求x-3y+4z的值.
解:由题意得:
x+2y=0,3x-6=0,5y+z=0
解得 x=2,y=-1,z=5
x-3y+4z
=2-3×(-1)+4×5
=25
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,
二是 ≥0.
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
五、课堂小结
六、布置作业
课本P27 习题2.3 第1,2,3,4题
六、布置作业
课本P27 习题2.3 第1,2,3,4题
谢谢聆听
第二章
实数
2.2 平方根(一)
请你说一说解决问题的思路.
学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?
一、情景导入
若正方形的面积如下,请填表:
思考:已知一个正数的平方,如何求这个正数?
正方形的面积/dm2
1
9
16
0.36
正方形的边长/dm2
一、情景导入
4
0.6
3
1
a2
a
例: ∵ 52=25,
∴ 5是25的算术平方根,即
二、探究新知
(一)概念学习
定义:如果一个正数x的平方等于a,即x2=a ,
那么这个正数x就叫做a的算术平方根.
(1)记作: ,读作:根号a
(2)规定:0的算术平方根是0,
(3) 表示求a的算术平方根
例1:求下列各数的算术平方根
(1)900; (2)1; (3) ; (4)0.04; (5)14
三、典例讲解
解:(1)∵ 302=900,
∴ 900是30的算术平方根,即
(2)∵ 12=1,
∴ 1是1的算术平方根,即
例1:求下列各数的算术平方根
(1)900; (2)1; (3) ; (4)0.04; (5)14
三、典例讲解
(4)∵ (0.2)2=0.04,
∴ 0.04是0.2的算术平方根,即
解:(3)∵ 2=
∴ 900是30的算术平方根,即
(5) 14的算术平方根,即
例2:求下各列的值
三、典例讲解
解:(1)∵ 82=64, ∴
(2)∵(0.7)2=0.49, ∴
(3)∵( )2 = , ∴
(4)∵ 132 = 169 , ∴
思考:
(1)-4有算术平方根吗?即有一个正数的平方等于-4吗?
(2)什么数才有算术平方根?
负数没有算术平方根;非负数才有算术平方根
(1)正数有一个正的算术平方根;
(2)0的算术平方根是0;
(3)负数没有算术平方根;
求算术平方根的方法:
非负数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
求a的算术平方根
x2=a
x的平方
互逆运算
例:
52=25
三、典例讲解
例3: 的算术平方根是 .
3
表示求a的算术平方根
的算术平方根是 .
a ≥ 0
(1)非负数才有算术平方根
≥ 0
(2)非负数的算术平方根是非负数
负数不存在算术平方根,
即当 a<0时, 无意义
式子 中的双重非负性:
(1)a≥0;
(2) ≥0.
算术平方根的性质:
判断:下列各式是否有意义,为什么?
(1) ;(2) ;(3) ;(4) .
解:(1)a=-4 <0,式子无意义;
(4)a=-(-5)=5 > 0,式子有意义.
(3)a=(-3)2=9 > 0,式子有意义;
(2)a=4 > 0,式子有意义;
三、典例讲解
例4:
若|a-3|+
的值为 。
,则代数式
-1
|a-3|≥0
≥0
∵ |a-3|+
a-3=0, b+4=0
a=3, b=-4
例5:自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9 t2.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?
解:将h=19.6代入公式
h=4.9 t2,
得 t2 =4,所以t =2(秒).
即铁球到达地面需要2秒.
三、典例讲解
1.16的算术平方根是 ( )
A. 2 B. 4 C. ±2 D. ±4
A
四、课堂检测
2. 2的算术平方根是 ( )
C
3.一个数的算术平方根是3,则这个数是( )
A. 3 B. 6
C. 9 D.
C
4.下列说法正确的是( )
A. 5是25的算术平方根B. -6是36的算术平方根
C. 0的算术平方根是0 D. 0.01是0.1的算术平方根
四、课堂检测
B
5. 下列各式表示正确的是 ( )
D
6. 小明房间的面积为10.8 m2,房间地面恰好由120块相同的正方形地砖铺成,则每块地砖的边长是 ( )
A. 0.3 m B. 0.45 m
C. 0.9 m D. 0.09 m
A
四、课堂检测
7. 下列结论正确的是 ( )
A
8. 若 ,则a=________;若 ,则a=__________.
10
-1
四、课堂检测
9.已知:|x+2y|+ +(5y+z)2=0
求x-3y+4z的值.
解:由题意得:
x+2y=0,3x-6=0,5y+z=0
解得 x=2,y=-1,z=5
x-3y+4z
=2-3×(-1)+4×5
=25
(1)算术平方根的概念,式子 中的双重非负性:
一是a≥0,
二是 ≥0.
(2)算术平方根的性质:
一个正数的算术平方根是一个正数;
0的算术平方根是0;
负数没有算术平方根.
(3)求一个正数的算术平方根的运算与平方运算是互逆的运算,利用这个互逆运算关系求非负数的算术平方根.
五、课堂小结
六、布置作业
课本P27 习题2.3 第1,2,3,4题
六、布置作业
课本P27 习题2.3 第1,2,3,4题
谢谢聆听
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
