人教版八年级上册数学:11.1.2 三角形的高、中线与角平分线 教案
文档属性
| 名称 | 人教版八年级上册数学:11.1.2 三角形的高、中线与角平分线 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 83.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-31 00:00:00 | ||
图片预览

文档简介
11.1.2
三角形的高、中线与角平分线
教
学
目
标
1.了解三角形的高、中线与角平分线的概念.
2.准确区分三角形的高、中线与角平分线.
3.能够独立完成与三角形的高、中线与角平分线有关的计算.
教学重点
1.了解三角形的高、中线与角平分线的概念.
2.能利用三角形的高、中线与角平分线的性质进行简单计算.
教学难点
1.能用自己的语言说出三角形的高、中线与角平分线的概念.
2.熟练运用三角形的高、中线与角平分线的性质进行有关计算.
环节
问题与情境
师生行为
明确目标
1.知道三角形的高、中线与角平分线的概念会,画三角形的高、中线、角平分线.
2.通过观察认识到三角形的三条高、三条中线、三条角平分线分别交于一点.
明确本节课的学习目标
探
究
过
程
精
讲
展
示
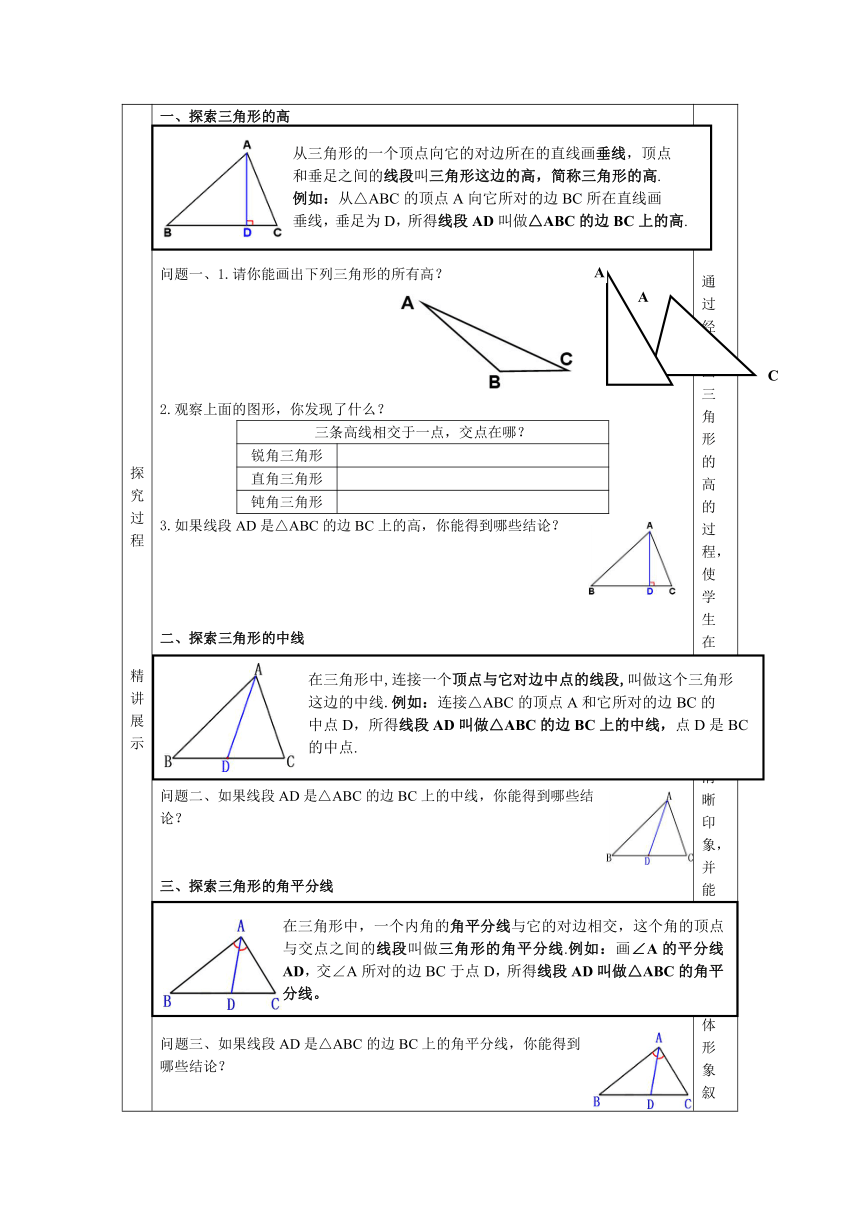
一、探索三角形的高
问题一、1.请你能画出下列三角形的所有高?
2.观察上面的图形,你发现了什么?
三条高线相交于一点,交点在哪?锐角三角形直角三角形钝角三角形
3.如果线段AD是△ABC的边BC上的高,你能得到哪些结论?
二、探索三角形的中线
问题二、如果线段AD是△ABC的边BC上的中线,你能得到哪些结论?
三、探索三角形的角平分线
问题三、如果线段AD是△ABC的边BC上的角平分线,你能得到哪些结论?
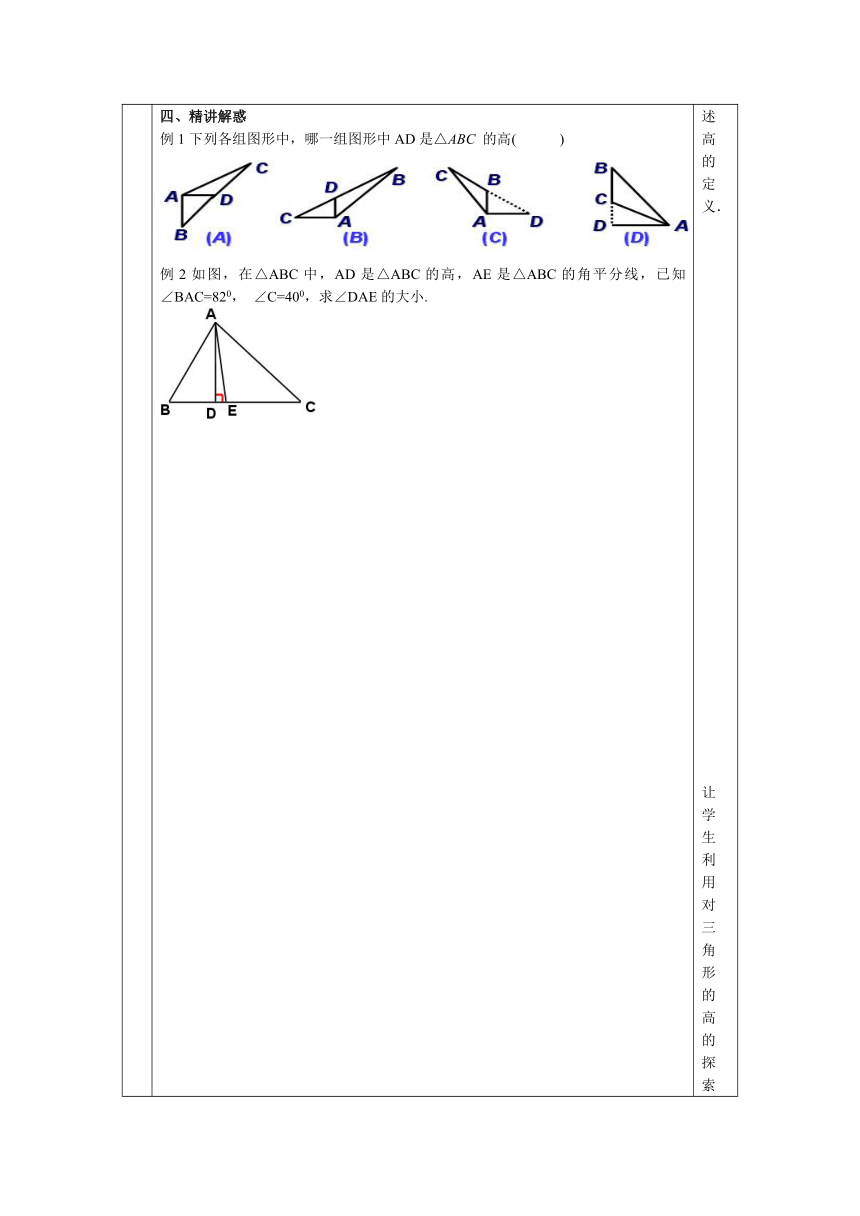
四、精讲解惑
例1下列各组图形中,哪一组图形中AD是△ABC
的高(
)
例2如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=820,
∠C=400,求∠DAE的大小.
通过经历画三角形的高的过程,使学生在头脑中留下清晰印象,并能结合这些具体形象叙述高的定义.
让学生利用对三角形的高的探索过程,利用类比的方法对三角形的中线、角平分线进行探究.
练
习
反
馈
五、课堂检测
1、如图1在△ABC中,BD⊥AC,EF∥AC,交BD于G,则下列结论错误的是(
)
A.BD是△ABC的高
B.CD是△BCD的高
C.EG是△ABD的高
D.BG是△BEF的高
2、如图2在△ABC中,BD=DE=EC,则AD,AE分别是
,
的中线.
3、如图3在ΔABC中,AE是中线,AD是角平分线,AF是高,(1)BE=
____
=
_____
;(2)∠BAD=
_____
=
___
;
(3)______
____=_______
__=90°;
图1
图2
图3
4、如图,在ΔABC中,BE是边AC上的中线,已知AB=4cm,AC=3cm,BE=5cm,求ΔABE的周长.
5、想一想,如何把一个三角形分成2个面积相等的三角形呢?
针对本节学习内容检测学生掌握情况,学生独立完成并讲解,让学生及时巩固所学知识,同时使得教师及时了解教学效果,查缺补漏.
总结
归纳
三角形的高、中线与角平分线的概念以及画法.
教师学生
共同梳理
总结
作业
练习卷.
教
学
后
记
三角形的高、中线与角平分线
教
学
目
标
1.了解三角形的高、中线与角平分线的概念.
2.准确区分三角形的高、中线与角平分线.
3.能够独立完成与三角形的高、中线与角平分线有关的计算.
教学重点
1.了解三角形的高、中线与角平分线的概念.
2.能利用三角形的高、中线与角平分线的性质进行简单计算.
教学难点
1.能用自己的语言说出三角形的高、中线与角平分线的概念.
2.熟练运用三角形的高、中线与角平分线的性质进行有关计算.
环节
问题与情境
师生行为
明确目标
1.知道三角形的高、中线与角平分线的概念会,画三角形的高、中线、角平分线.
2.通过观察认识到三角形的三条高、三条中线、三条角平分线分别交于一点.
明确本节课的学习目标
探
究
过
程
精
讲
展
示
一、探索三角形的高
问题一、1.请你能画出下列三角形的所有高?
2.观察上面的图形,你发现了什么?
三条高线相交于一点,交点在哪?锐角三角形直角三角形钝角三角形
3.如果线段AD是△ABC的边BC上的高,你能得到哪些结论?
二、探索三角形的中线
问题二、如果线段AD是△ABC的边BC上的中线,你能得到哪些结论?
三、探索三角形的角平分线
问题三、如果线段AD是△ABC的边BC上的角平分线,你能得到哪些结论?
四、精讲解惑
例1下列各组图形中,哪一组图形中AD是△ABC
的高(
)
例2如图,在△ABC中,AD是△ABC的高,AE是△ABC的角平分线,已知∠BAC=820,
∠C=400,求∠DAE的大小.
通过经历画三角形的高的过程,使学生在头脑中留下清晰印象,并能结合这些具体形象叙述高的定义.
让学生利用对三角形的高的探索过程,利用类比的方法对三角形的中线、角平分线进行探究.
练
习
反
馈
五、课堂检测
1、如图1在△ABC中,BD⊥AC,EF∥AC,交BD于G,则下列结论错误的是(
)
A.BD是△ABC的高
B.CD是△BCD的高
C.EG是△ABD的高
D.BG是△BEF的高
2、如图2在△ABC中,BD=DE=EC,则AD,AE分别是
,
的中线.
3、如图3在ΔABC中,AE是中线,AD是角平分线,AF是高,(1)BE=
____
=
_____
;(2)∠BAD=
_____
=
___
;
(3)______
____=_______
__=90°;
图1
图2
图3
4、如图,在ΔABC中,BE是边AC上的中线,已知AB=4cm,AC=3cm,BE=5cm,求ΔABE的周长.
5、想一想,如何把一个三角形分成2个面积相等的三角形呢?
针对本节学习内容检测学生掌握情况,学生独立完成并讲解,让学生及时巩固所学知识,同时使得教师及时了解教学效果,查缺补漏.
总结
归纳
三角形的高、中线与角平分线的概念以及画法.
教师学生
共同梳理
总结
作业
练习卷.
教
学
后
记
